Дедукция википедия: дедукция — Викисловарь
дедукция — Викисловарь
Морфологические и синтаксические свойства
| падеж | ед. ч. | мн. ч. |
|---|---|---|
| Им. | деду́кция | деду́кции |
| Р. | деду́кции | деду́кций |
| Д. | деду́кции | деду́кциям |
| В. | деду́кцию | деду́кции |
| Тв. | деду́кцией деду́кциею | деду́кциями |
| Пр. | деду́кции | деду́кциях |
де-ду́к-ци·я
Существительное, неодушевлённое, женский род, 1-е склонение (тип склонения 7a по классификации А. А. Зализняка).
Корень: -дедукц-; суффикс: -иj; окончание: -я [Тихонов, 1996].
Произношение
- МФА: [dʲɪˈdukt͡sɨɪ̯ə]
Семантические свойства
Значение
- филос. метод рассуждения от общих положений к частным, логический вывод частных положений из какой-либо общей мысли ◆ Считается, что если посылки дедукции истинны, то истинны и её следствия. Дедукция ― одно из основных средств доказательства. Владимир Горбачев, «Концепции современного естествознания», 2003 г. (цитата из Национального корпуса русского языка, см. Список литературы)
- в логике переход от посылок к заключению, опирающийся на логический закон, в силу чего заключение с логической необходимостью следует из принятых посылок ◆ Традиционная теория формальной логики, которая разрывала взаимосвязь дедукции и индукции и целиком сводила умозаключения к дедукции, выносила общее положение из единичного контекста и считала, что всякий вывод совершается на основании предшествующих ему общих положений. С. Л. Рубинштейн, «Основы общей психологии», 1940 г. (цитата из Национального корпуса русского языка, см. Список литературы)
Синонимы
- —
- вывод
Антонимы
- индукция
Гиперонимы
Гипонимы
Родственные слова
Этимология
Происходит от лат. deductio «отведение, увод; выведение, дедукция», от гл. deducere «спускать вниз; уводить, отводить; выводить, производить», далее из de «из, от», из праиндоевр. *de- + dūcere «водить, вести» (восходит к праиндоевр. *deuk- «вести»).
Фразеологизмы и устойчивые сочетания
Перевод
Библиография
 | Для улучшения этой статьи желательно:
|
Морфологические и синтаксические свойства
| Ед. | дедукция |
| Ед. об. | дедукция |
| Ед. суб. | дедукцията |
| Мн. | дедукции |
| Мн. сов. | дедукциите |
| Числ. | — |
| Зв. | — |
дедукция
Существительное, женский род, склонение 47.
Корень: —.
Произношение
Семантические свойства
Значение
- филос. дедукция (аналогично русскому слову) ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы
- частичн.: извод, заключение, умозаключение
Антонимы
Гиперонимы
Гипонимы
Родственные слова
| Ближайшее родство | |
Этимология
От ??
Фразеологизмы и устойчивые сочетания
Дедукція — Вікіпедія
Матеріал з Вікіпедії — вільної енциклопедії.
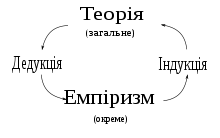 Схема класичного уявлення зв’язку між теорією, емпіризмом, індукцією та дедукцією.
Схема класичного уявлення зв’язку між теорією, емпіризмом, індукцією та дедукцією.
Деду́кція — процес виведення висновку, що гарантовано слідує, якщо вихідні припущення істинні, то висновок на їх підставі є чинним (див. правильність). Висновок повинен базуватись винятково на основі попередньо наведених доказів та не повинен містити нової інформації про предмет, що досліджується. Дедукція була вперше описана у працях давньогрецьких філософів, таких як Арістотель.[1]Процес виведення дедуктивно правильний тоді і лише тоді, коли з точки зору логіки за умови істинності вихідних припущень висновки також істинні; або, логічно неможливі хибні висновки за правильних припущень.[2]
Дедуктивний, (англ. deductive, нім. deduktiv) — заснований на дедукції; дедуктивний метод — спосіб дослідження, при якому окремі положення логічно виводяться із загальних положень (аксіом, постулатів, законів).
У логіці використовуються два загальних методи отримання висновків: дедукція та індукція. Головною відмінністю індукції є те що для її застосування не вимагається знати усі факти до того як зробити висновок. Оскільки на практиці неможливо все з’ясувати перед тим як робити умовивід, дедукція не має широкого застосування у реальному світі, окрім математики й природничих наук, які використовують математичні методи. Індукція, натомість, оперує набором неповних фактів, та на їх основі робить висновок який напевно випливає, не даючи жодних гарантій щодо його істинності. Попри це, індукція дає можливість набувати нових знань, котрі не є очевидними при розгляді вихідних тверджень.
Часто зустрічається помилкова думка, що дедукція рухається від загального до окремого та що індукція — це рух у зворотньому напрямку.
Нехай γ{\displaystyle \gamma } — множина формул, а ϕ{\displaystyle \phi } — одна формула формальної мови. Дедукційна система S{\displaystyle S} може складатись з переліку аксіом та правил висновування. Твердження <γ,ϕ>{\displaystyle <\gamma ,\phi >} формальною мовою дедуктивно правильне, якщо існує послідовність формул в формальній мові, що завершується ϕ{\displaystyle \phi }, така, що кожен член послідовності є або елементом з γ{\displaystyle \gamma }, аксіомою з S{\displaystyle S}, або виводиться з попередніх формул послідовності через правило висновування S{\displaystyle S}. Якщо <γ,ϕ>{\displaystyle <\gamma ,\phi >} правильне в S{\displaystyle S}, то записують γ⊢Sϕ{\displaystyle \gamma \vdash _{S}\phi }, або просто γ⊢ϕ{\displaystyle \gamma \vdash \phi }.[2]
Нехай σ{\displaystyle \sigma } — вислів. Позначимо через fσ{\displaystyle f_{\sigma }} твердження «σ{\displaystyle \sigma } не правильне», а через tσ{\displaystyle t_{\sigma }} — твердження «σ{\displaystyle \sigma } правильне».
Нехай
- σ,ϕ1,ϕ2,…,ϕn,…{\displaystyle \sigma ,\phi _{1},\phi _{2},\dots ,\phi _{n},\dots } — скінченна або нескінченна послідовність висловів. Вислів σ{\displaystyle \sigma } називається дедуктивно виводимим за Бетом із висловів ϕ1,…,ϕn,…{\displaystyle \phi _{1},\dots ,\phi _{n},\dots }, якщо існує семантична таблиця з протиріччям, побудована таким чином:[3]
Якщо послідовність висловів нескінченна, то така побудова може ніколи не завершитись. Вислів σ{\displaystyle \sigma } дедуктивно виводимий за Бетом тоді і лише тоді, якщо побудова завершується, і в результаті отримується семантична таблиця з протиріччям.
Якщо вислів σ{\displaystyle \sigma } дедуктивно виводимий за Бетом із висловів ϕ1,…,ϕn{\displaystyle \phi _{1},\dots ,\phi _{n}} то σ{\displaystyle \sigma } є логічним наслідком висловів ϕ1,…,ϕn{\displaystyle \phi _{1},\dots ,\phi _{n}}. Формально це записується:[3]
- {ϕ1,…,ϕn}⊢Bσ⇒{ϕ1,…,ϕn}⊨σ.{\displaystyle \{\phi _{1},\dots ,\phi _{n}\}\vdash _{B}\sigma \Rightarrow \{\phi _{1},\dots ,\phi _{n}\}\models \sigma .}
Якщо вислів σ{\displaystyle \sigma } є логічним наслідком висловів ϕ1,…,ϕn{\displaystyle \phi _{1},\dots ,\phi _{n}}, то σ{\displaystyle \sigma } логічно виводиться за Бетом із висловів ϕ1,…,ϕn{\displaystyle \phi _{1},\dots ,\phi _{n}}. Формально це записується:
- {ϕ1,…,ϕn}⊨σ⇒{ϕ1,…,ϕn}⊢Bσ.{\displaystyle \{\phi _{1},\dots ,\phi _{n}\}\models \sigma \Rightarrow \{\phi _{1},\dots ,\phi _{n}\}\vdash _{B}\sigma .}
- ↑ «Філософський словник» / За ред. В. І. Шинкарука. — 2.вид., перероб. і доп. — К.: Голов. Ред. УРЕ, 1986.
- ↑ а б Jacquette, Dale (2002). A companion to philosophical logic. Malden, Mass.: Blackwell. ISBN 0-631-21671-5.
- ↑ а б (Метакидес, 1998; с. 63)
Дедукция Википедия
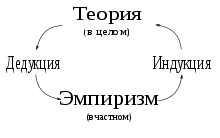 Схема классического представления связи между теорией, эмпиризмом, индукцией и дедукцией.
Схема классического представления связи между теорией, эмпиризмом, индукцией и дедукцией.
Деду́кция (лат. deductio — выведение[1], также дедуктивное умозаключение, силлогизм[2]) — метод мышления, следствием которого является логический вывод, истинность которого гарантируется истинностью посылок. Также может определяться логико-методологическая процедура, посредством которой осуществляется переход от общего к частному в процессе рассуждения.
Началом (посылками) дедукции являются аксиомы или просто гипотезы, имеющие характер общих утверждений («общее»), а концом — следствия из посылок, теоремы («частное»). Если посылки дедукции истинны, то истинны и её следствия. Дедукция — основное средство логического доказательства. Противоположно индукции.
Пример простейшего дедуктивного умозаключения:
| Все люди смертны. | |
| Сократ — человек. | |
| Дедукция | Сократ смертен. |
Условно-категорические умозаключения[ | ]
Умозаключения, в которых одна предпосылка является условным суждением, а вторая предпосылка совпадает с основанием или следствием условного суждения или же с результатом отрицания основания или следствия условного суждения.
Истинность основы влечёт истинность следствия, а отрицание следствия влечёт отрицание основы.
Формы правильных модусов (видов) условно-категорических заключений:
Разделительно-категорические умозаключения[ | ]
ДЕДУКЦИЯ — это… Что такое ДЕДУКЦИЯ?
ДЕДУКЦИЯ — (от лат. deductio выведение) переход от посылок к заключению, опирающийся на логический закон, в силу чего заключение с логической необходимостью следует из принятых посылок. Характерная особенность Д. заключается в том, что от истинных посылок… … Философская энциклопедия
ДЕДУКЦИЯ — (лат. deductio, от deducere выводить). Вывод частных фактов из общих основных положений. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ДЕДУКЦИЯ [лат. deductio выведение] лог. способ рассуждения, при котором новое … Словарь иностранных слов русского языка
дедукция — и, ж. déduction f., нем. Deduktion <лат. deductio выведение. 1. дипл. Изложение, изъяснение чего л. Сл. 18. Шведы против сего мира пространную дедукцию писменно Королю подали. ЖПВ 2 493. Министерство потом вручило ему письменную дедукцию своих … Исторический словарь галлицизмов русского языка
Дедукция — Дедукция ♦ Déduction Рассуждать методом дедукции значит выводить из истинных или предположительно истинных суждений (принципов или предпосылок) другие суждения, с необходимостью из них вытекающие. Под дедукцией, пишет Декарт, мы понимаем… … Философский словарь Спонвиля
дедукция — (от лат. deductio выведение) движение знания от более общего к менее общему, частному, выведение следствия из посылок. Д. тесно связана с индукцией. Логика рассматривает Д. как вид умозаключения. Психология изучает развитие и нарушение… … Большая психологическая энциклопедия
Дедукция — (лат. deductio шығару) бастапқы пайымдаулар (алғышарттар) жиынтығынан қажетті шығарылатын салдарларды алатын рационалды танымның әдісі. Дедукция процесінде пікірлердің тек логикалық қатал, әдепті (корректный) амалдары – логикалық формалары −… … Философиялық терминдердің сөздігі
ДЕДУКЦИЯ — (от латинского deductio выведение), вывод по правилам логики; цепь умозаключений (рассуждение), звенья которой (высказывания) связаны отношением логического следования. Началом (посылками) дедукции являются аксиомы, постулаты или гипотезы,… … Современная энциклопедия
ДЕДУКЦИЯ — (от лат. deductio выведение) вывод по правилам логики; цепь умозаключений (рассуждение), звенья которой (высказывания) связаны отношением логического следования. Началом (посылками) дедукции являются аксиомы, постулаты или просто гипотезы,… … Большой Энциклопедический словарь
Дедукция — Дедукция (лат. deductio выведение) метод мышления, при котором частное положение логическим путем выводится из общего, вывод по правилам логики; цепь умозаключений (рассуждение), звенья которой (высказывания) связаны отношением логического… … Википедия
дедукция — выведение, вывод, умозаключение, заключение Словарь русских синонимов. дедукция сущ., кол во синонимов: 3 • вывод (31) • … Словарь синонимов
дедукция — спец. ДЕДУКЦИЯ, вывод, книжн. умозаключение ВЫВОД, заключение, книжн. умозаключение ВЫВОДИТЬ/ВЫВЕСТИ, заключать/заключить, книжн. умозаключать/умозаключить … Словарь-тезаурус синонимов русской речи
ДЕДУКЦИЯ — Новая философская энциклопедия
ДЕДУКЦИЯ (от лат. deductio – выведение) – переход от общего к частному; в более специальном смысле термин «дедукция» обозначает процесс логического вывода, т.е. перехода по тем или иным правилам логики от некоторых данных предложений-посылок к их следствиям (заключениям). Термин «дедукция» употребляется и для обозначения конкретных выводов следствий из посылок (т.е. как синоним термина «вывод» в одном из его значений), и как родовое наименование общей теории построений правильных выводов. Науки, предложения которых преимущественно получаются как следствия некоторых общих принципов, постулатов, аксиом, принято называть дедуктивными (математика, теоретическая механика, некоторые разделы физики и др.), а аксиоматический метод, посредством которого производятся выводы этих частных предложений, – аксиоматико-дедуктивным.
Изучение дедукции составляет задачу логики; иногда формальную логику даже определяют как теорию дедукции.
Хотя термин «дедукция» впервые употреблен, по-видимому, Боэцием, понятие дедукции – как доказательство какого-либо предложения посредством силлогизма – фигурирует уже у Аристотеля («Первая Аналитика»). В философии и логике Нового времени существовали различные взгляды на роль дедукции в ряду методов познания. Так, Декарт противопоставлял дедукции интуицию, посредством которой, по его мнению, разум «непосредственно усматривает» истину, в то время как дедукция доставляет разуму лишь «опосредованное» (полученное путем рассуждения) знание. Ф.Бэкон, а позднее и др. английские логики-«индуктивисты» (У.Уэвелл, Дж.С.Милль, А.Бэн и др.) считали дедукцию «второстепенным» методом, в то время как подлинное знание дает только индукция. Лейбниц и Вольф, исходя из того, что дедукция не дает «новых фактов», именно на этом основании приходили к прямо противоположному выводу: полученные путем дедукции знания являются «истинными во всех возможных мирах». Взаимосвязь дедукции и индукции была раскрыта Ф.Энгельсом, который писал, что «индукция и дедукция связаны между собой столь же необходимым образом, как синтез и анализ. Вместо того чтобы односторонне превозносить одну из них до небес за счет другой, надо стараться применять каждую из них на своем месте, а этого можно добиться лишь в том случае, если не упускать из виду их связь между собой, их взаимное дополнение друг друга» (Маркс К., Энгельс Ф. Соч., т. 20, с. 542–543).
В формальной логике к системе логических правил и к их применениям в любой области относится следующее положение: все, что заключено в любой полученной посредством дедуктивного умозаключения логической истине, содержится уже в посылках, из которых она выведена. Каждое применение правила состоит в том, что общее положение относится (применяется) к некоторой конкретной (частной) ситуации. Некоторые правила логического вывода подпадают под такую характеристику и совсем явным образом. Так, напр., различные модификации т.н. правила подстановки гласят, что свойство доказуемости (или выводимости из данной системы посылок) сохраняется при любой замене элементов произвольной формулы данной формальной теории конкретными выражениями того же вида. То же относится к распространенному способу задания аксиоматических систем посредством т.н. схем аксиом, т.е. выражений, обращающихся в конкретные аксиомы после подстановки вместо входящих в них общих обозначений конкретных формул данной теории. Под дедукцией часто понимают и сам процесс логического следования. Это обусловливает его тесную связь с понятиями вывода и следствия, находящую свое отражение и в логической терминологии. Так, «теоремой о дедукции» принято называть одно из важных соотношений между логической связкой импликации (формализующей словесный оборот «если… то…») и отношением логического следования (выводимости): если из посылки А выводится следствие В, то импликация А⊃В («если А… то В…») доказуема (т.е. выводима уже без всяких посылок, из одних только аксиом). Аналогичный характер носят и др. связанные с понятием дедукции логические термины. Так, дедуктивно-эквивалентными называют предложения, выводимые друг из друга; дедуктивная полнота системы (относительно какого-либо свойства) состоит в том, что все выражения данной системы, обладающие этим свойством (напр., истинностью при некоторой интерпретации), доказуемы в ней.
Свойства дедукции раскрывались в ходе построения конкретных логических формальных систем (исчислений) и обшей теории таких систем (т.н. теории доказательства).
Литература:
1. Тарский А. Введение в логику и методологию дедуктивных наук, пер. с англ. М., 1948;
2. Асмус В.Ф. Учение логики о доказательстве и опровержении. М., 1954.
Источник:
Новая философская энциклопедия
на Gufo.me
Значения в других словарях
- дедукция —
Деду́кц/и/я [й/а].
Морфемно-орфографический словарь - дедукция —
Дедукции, мн. нет, ж. [латин. deductio – выведение] (науч.). Метод мышления, при к-ром новое положение выводится чисто логическим путем из предшествующих; противоп. индукция.
Большой словарь иностранных слов - Дедукция —
(лат. deductio — выведение) переход от общего знания о предметах данного класса к единичному (частному) знанию об отдельном предмете этого класса; один из методов познания. Д. — осн. средство доказательства.
Педагогический терминологический словарь - дедукция —
ДЕД’УКЦИЯ, дедукции, мн. нет, ·жен. (·лат. deductio — выведение) (научн.). Метод мышления, при котором новое положение выводится чисто логическим путем из предшествующих; ант. индукция.
Толковый словарь Ушакова - ДЕДУКЦИЯ —
ДЕДУКЦИЯ (лат. deductio — выведение) — в широком смысле слова способ рассуждения, при котором осуществляется переход от знания общего к знанию частному или единичному. В этом смысле…
Новейший философский словарь - дедукция —
-и, ж. лог. Способ рассуждения от общих положений к частным, логический вывод частных положений из какой-л. общей мысли; противоп. индукция. [лат. deductio]
Малый академический словарь - ДЕДУКЦИЯ —
(от лат. deductio — выведение) — 1) процесс логического вывода, т. е. перехода от посылок к заключениям в соответствии с правилами логики; 2) конкретный вывод; 3) родовое наименование общей теории построения правильных умозаключений…
Большой психологический словарь - дедукция —
орф. дедукция, -и
Орфографический словарь Лопатина - Дедукция —
(от лат. deductio — выведение) переход от общего к частному; в более специальном смысле термин «Д.» обозначает процесс логического вывода, т. е. перехода по тем или иным правилам логики (См.
Большая советская энциклопедия - дедукция —
ДЕДУКЦИЯ -и; ж. [лат. deductio] Лог. Способ рассуждения от общих положений к частным, логический вывод частных положений из какой-л. общей мысли (противоп.: индукция). ◁ Дедуктивный, -ая, -ое.
Толковый словарь Кузнецова - дедукция —
ДЕДУКЦИЯ, и, ж. Способ рассуждения от общих положений к частным выводам; противоп. индукция. | прил. дедуктивный, ая, ое.
Толковый словарь Ожегова - ДЕДУКЦИЯ —
ДЕДУКЦИЯ (от лат. deductio — выведение) — англ. deduction; нем. Deduktion. 1. Одна из форм умозаключения от общего к частному и единичному, характеризующаяся тем, что новое знание о к.-л.
Социологический словарь - дедукция —
дедукция ж. Логическое умозаключение, переход от общих положений, законов и т.п. к частному, конкретному выводу. || противоп. индукция
Толковый словарь Ефремовой - дедукция —
Дедукция, дедукции, дедукции, дедукций, дедукции, дедукциям, дедукцию, дедукции, дедукцией, дедукциею, дедукциями, дедукции, дедукциях
Грамматический словарь Зализняка - Дедукция —
(от deducere — выводить) — термин современной логики, обозначающий выведение одной мысли из другой, делаемое на основании логических законов. Большинство логиков под словом…
Энциклопедический словарь Брокгауза и Ефрона - дедукция —
ДЕДУКЦИЯ и, ж. déduction f., нем. Deduktion <�лат. deductio выведение. 1. дипл. Изложение, изъяснение чего-л. Сл. 18. Шведы против сего мира пространную дедукцию писменно Королю подали. ЖПВ 2 493.
Словарь галлицизмов русского языка - дедукция —
ДЕДУКЦИЯ (от лат. deductio — выведение). — В современной логике термин «Д .» используется как синоним более точного, но более громоздкого термина «дедуктивно правильное рассуждение».
Энциклопедия эпистемологии и философии науки - ДЕДУКЦИЯ —
ДЕДУКЦИЯ (от лат. deductio — выведение) — вывод по правилам логики; цепь умозаключений (рассуждение) — звенья которой (высказывания) связаны отношением логического следования.
Большой энциклопедический словарь - дедукция —
сущ., кол-во синонимов: 3 вывод 31 следствие 18 умозаключение 17
Словарь синонимов русского языка

Дедукция — это… Что такое Дедукция?
переход от общего к частному; в более специальном смысле термин «Д.» обозначает процесс логического вывода, т. е. перехода по тем или иным правилам логики (См. Логика) от некоторых данных предложений — посылок к их следствиям (заключениям), причём в некотором смысле следствия всегда можно характеризовать как «частные случаи» («примеры») общих посылок. Термин «Д.» употребляется и для обозначения конкретных выводов следствий из посылок (т. е. как синоним термина «вывод» в одном из его значений), и — чаще — как родовое наименование общей теории построений правильных выводов (умозаключений (См. Умозаключение)). В соответствии с этим последним словоупотреблением, науки, предложения которых получаются (хотя бы преимущественно) как следствия некоторых общих «базисных законов» (принципов, постулатов, аксиом и т.п.), принято называть дедуктивными (математика, теоретическая механика, некоторые разделы физики и др.), а Аксиоматический метод, посредством которого производятся выводы этих частных предложений, часто называют аксиоматико-дедуктивным.
Изучение Д. составляет главную задачу логики; иногда логику — во всяком случае логику формальную — даже определяют как «теорию Д.», хотя логика далеко не единственная наука, изучающая методы Д.: Психология изучает реализацию Д. в процессе реального индивидуального мышления и его формирования, а гносеология (Теория познания) — как один из основных (наряду с другими, в частности различными формами индукции (См.
Индукция)) методов научного познания мира.
Хотя сам термин «Д.» впервые употреблён, по-видимому, Боэцием (См. Боэций), понятие Д. — как Доказательство какого-либо предложения посредством Силлогизма — фигурирует уже у Аристотеля (См. Аристотель) («Первая Аналитика»). В философии и логике средних веков и нового времени имели место значительные расхождения во взглядах на роль Д. в ряду др. методов познания. Так, Р. Декарт противопоставлял Д. интуиции (См. Интуиция), посредством которой, по его мнению, человеческий разум «непосредственно усматривает» истину, в то время как Д. доставляет разуму лишь «опосредованное» (полученное путём рассуждения) знание. (Провозглашённый Декартом примат интуиции над Д. возродился гораздо позже и в значительно изменённых и развитых формах в концепциях так называемого интуиционизма.) Ф. Бэкон, а позднее др. английские логики-«индуктивисты»(У. Уэвелл, Дж. С. Милль, А. Бэн и др.), справедливо отмечая, что в заключении, полученном посредством Д., не содержится (если выражаться на современном языке) никакой «информации», которая не содержалась бы (пусть неявно) в посылках, считали на этом основании Д. «второстепенным» методом, в то время как подлинное знание, по их мнению, даёт только индукция. Наконец, представители направления, идущего в первую очередь от немецкой философии (X. Вольф, Г. В. Лейбниц), также, исходя по сути дела из того, что Д. не даёт «новых» фактов, именно на этом основании приходили к прямо противоположному выводу: полученные путём Д. знания являются «истинными во всех возможных мирах» (или, как говорил позже И. Кант, «аналитически истинными»), чем и определяется их «непреходящая» ценность [в отличие от полученных индуктивным обобщением данных наблюдения и опыта «фактических» («синтетических») истин, верных, так сказать, «лишь в силу стечения обстоятельств»].
С современной точки зрения вопрос о взаимных «преимуществах» Д. или индукции в значительной мере утратил смысл. Уже Ф. Энгельс писал, что «индукция и дедукция связаны между собой столь же необходимым образом, как синтез и анализ. Вместо того чтобы односторонне превозносить одну из них до небес за счет другой, надо стараться применять каждую из них на своем месте, а этого можно добиться лишь в том случае, если не упускать из виду их связь между собой, их взаимное дополнение друг друга» («Диалектика природы», 1969, с. 195 — 196). Однако и независимо от отмечаемой здесь диалектической взаимосвязи Д. и индукции и их применений изучение принципов Д. имеет громадное самостоятельное значение. Именно исследование этих принципов как таковых и составило по существу основное содержание всей формальной логики — от Аристотеля до наших дней. Более того, в настоящее время всё активнее ведутся работы по созданию различных систем «индуктивной логики», причём (такова диалектика этих на первый взгляд полярных понятий) своего рода идеалом здесь представляется создание «дедуктивноподобных» систем, т. е. совокупностей таких правил, следуя которым можно было бы получать заключения, имеющие если не 100%-ную достоверность (как знания, полученные путём Д.), то хотя бы достаточно большую «степень правдоподобия», или «вероятность» (см. Вероятностная логика).
Что же касается формальной логики в более узком смысле этого термина, то как к самой по себе системе логических правил, так и к любым их применениям в любой области в полной мере относится положение о том, что всё, что заключено в любой полученной посредством дедуктивного умозаключения «аналитической (или «логической») истине», содержится уже в посылках, из которых она выведена: каждое применение правила в том и состоит, что общее положение относится (применяется, прилагается) к некоторой конкретной («частной») ситуации. Некоторые правила логического вывода подпадают под такую характеристику и совсем явным образом; например, различные модификации так называемого правила подстановки гласят, что свойство доказуемости (или выводимости из данной системы посылок) сохраняется при любой замене элементов произвольной формулы данной формальной теории «конкретными» выражениями «того же вида». То же относится к распространённому способу задания аксиоматических систем посредством так называемых схем аксиом, т. е. выражений, обращающихся в «конкретные» аксиомы после подстановки вместо входящих в них «родовых» обозначений конкретных формул данной теории.
Но какой бы конкретный вид ни имело данное правило, любое его применение всегда носит характер Д. «Непреложность», обязательность, «формальность» правил логики, не ведающая никаких исключений, таит в себе богатейшие возможности автоматизации самого процесса логического вывода с использованием ЭВМ (см. Алгоритм, Кибернетика).
Под Д. часто понимают и сам процесс логического следования. Это обусловливает тесную связь (а иногда даже отождествление) понятия Д. с понятиями вывода и следствия, находящую своё отражение и в логической терминологии; так, «теоремой о Д.» принято называть одно из важных соотношений между логической связкой импликации (формализующей словесный оборот «Если…, то… ») и отношением логического следования (выводимости): если из посылки А выводится следствие В, то импликация А ⊃ В («Если А…, то В…») доказуема (т. е. выводима уже без всяких посылок, из одних только аксиом). (Теорема о Д., справедливая при некоторых достаточно общих условиях для всех «полноценных» логических систем, в некоторых случаях просто постулируется для них в качестве исходного правила.) Аналогичный характер носят и другие связанные с понятием Д. логические термины; так, дедуктивно эквивалентными называются предложения, выводимые друг из друга; дедуктивная полнота системы (относительно какого-либо свойства) состоит в том, что все выражения данной системы, обладающие этим свойством (например, истинностью при некоторой интерпретации (См. Интерпретация)), доказуемы в ней.
Свойства Д. — это по сути дела свойства отношения выводимости. Поэтому и раскрывались они преимущественно в ходе построения конкретных логических (и логико-математических) формальных систем (исчислений (См. Исчисление)) и общей теории таких систем (так называемой теории доказательства). Большой вклад в это изучение внесли: создатель формальной логики Аристотель и др. античные учёные; выдвинувший идею формального логического исчисления (и справедливо считающийся провозвестником математической логики) Г. В. Лейбниц; создатели первых алгебрологических систем Дж. Буль, У. Джевонс, П. С. Порецкий, Ч. Пирс; создатели первых логико-математических аксиоматических систем Дж. Пеано, Г. Фреге, Б. Рассел; наконец, идущая от Д. Гильберта школа современных исследователей (К. Гёдель, А. Чёрч, Ж. Эрбран и др.), включая создателей теории Д. в виде так называемых исчислений естественного вывода (или «натуральной Д.») немецкого логика Г. Генцена, польского логика С. Яськовского и нидерландского логика Э. Бета. Теория Д. активно разрабатывается и в настоящее время, в том числе и в СССР (П. С. Новиков, А. А. Марков, Н. А. Шанин, А. С. Есенин-Вольпин и др.).
Лит.: Аристотель, Аналитики первая и вторая, пер. с греч., М., 1952; Декарт P., Правила для руководства ума, пер. с. лат., М. — Л., 1936; его же, Рассуждение о методе, М., 1953; Лейбниц Г. В., Новые опыты о человеческом разуме М. — Л., 1936; Тарский А., Введение в логику и методологию дедуктивных наук, пер. с англ., М., 1948; Асмус В. Ф., Учение логики о доказательстве и опровержении, М., 1954.
Ю. А. Гастев.
ДЕДУКЦИЯ — это… Что такое ДЕДУКЦИЯ?
ДЕДУКЦИЯ — (от лат. deductio выведение) переход от посылок к заключению, опирающийся на логический закон, в силу чего заключение с логической необходимостью следует из принятых посылок. Характерная особенность Д. заключается в том, что от истинных посылок… … Философская энциклопедия
ДЕДУКЦИЯ — (лат. deductio, от deducere выводить). Вывод частных фактов из общих основных положений. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ДЕДУКЦИЯ [лат. deductio выведение] лог. способ рассуждения, при котором новое … Словарь иностранных слов русского языка
дедукция — и, ж. déduction f., нем. Deduktion <лат. deductio выведение. 1. дипл. Изложение, изъяснение чего л. Сл. 18. Шведы против сего мира пространную дедукцию писменно Королю подали. ЖПВ 2 493. Министерство потом вручило ему письменную дедукцию своих … Исторический словарь галлицизмов русского языка
Дедукция — Дедукция ♦ Déduction Рассуждать методом дедукции значит выводить из истинных или предположительно истинных суждений (принципов или предпосылок) другие суждения, с необходимостью из них вытекающие. Под дедукцией, пишет Декарт, мы понимаем… … Философский словарь Спонвиля
дедукция — (от лат. deductio выведение) движение знания от более общего к менее общему, частному, выведение следствия из посылок. Д. тесно связана с индукцией. Логика рассматривает Д. как вид умозаключения. Психология изучает развитие и нарушение… … Большая психологическая энциклопедия
Дедукция — (лат. deductio шығару) бастапқы пайымдаулар (алғышарттар) жиынтығынан қажетті шығарылатын салдарларды алатын рационалды танымның әдісі. Дедукция процесінде пікірлердің тек логикалық қатал, әдепті (корректный) амалдары – логикалық формалары −… … Философиялық терминдердің сөздігі
ДЕДУКЦИЯ — (от латинского deductio выведение), вывод по правилам логики; цепь умозаключений (рассуждение), звенья которой (высказывания) связаны отношением логического следования. Началом (посылками) дедукции являются аксиомы, постулаты или гипотезы,… … Современная энциклопедия
ДЕДУКЦИЯ — (от лат. deductio выведение) вывод по правилам логики; цепь умозаключений (рассуждение), звенья которой (высказывания) связаны отношением логического следования. Началом (посылками) дедукции являются аксиомы, постулаты или просто гипотезы,… … Большой Энциклопедический словарь
Дедукция — Дедукция (лат. deductio выведение) метод мышления, при котором частное положение логическим путем выводится из общего, вывод по правилам логики; цепь умозаключений (рассуждение), звенья которой (высказывания) связаны отношением логического… … Википедия
дедукция — выведение, вывод, умозаключение, заключение Словарь русских синонимов. дедукция сущ., кол во синонимов: 3 • вывод (31) • … Словарь синонимов
дедукция — спец. ДЕДУКЦИЯ, вывод, книжн. умозаключение ВЫВОД, заключение, книжн. умозаключение ВЫВОДИТЬ/ВЫВЕСТИ, заключать/заключить, книжн. умозаключать/умозаключить … Словарь-тезаурус синонимов русской речи
Deduktion — Wikipedia
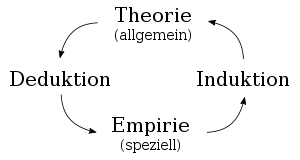 In einer klassischen Darstellung der empirischen Sozialwissenschaften bilden Deduktion, Induktion, Theorie und Empirie zentrale Begriffe. Dabei werden in der Empirie Daten erhoben, aus diesen per Induktion allgemeine Sätze (Theorie) gewonnen, aus der Theorie wiederum können per Deduktion Aussagen über Einzelfälle gewonnen werden.
In einer klassischen Darstellung der empirischen Sozialwissenschaften bilden Deduktion, Induktion, Theorie und Empirie zentrale Begriffe. Dabei werden in der Empirie Daten erhoben, aus diesen per Induktion allgemeine Sätze (Theorie) gewonnen, aus der Theorie wiederum können per Deduktion Aussagen über Einzelfälle gewonnen werden.
Die Deduktion (lateinisch deductio ‚Abführen, Fortführen, Ableitung‘), а также deduktive Methode или deduktiver Schluss , istung derussischée logis en dérésénés en dér.Deduktion ist schon bei Aristoteles als „Schluss vom Allgemeinen auf das Besondere“ verstanden worden, d. час der Vererbung von Eigenschaften, die all Mitglieder einer Gruppe teilen, auf echte Untermengen und einzelne Elemente. Dem stellt Aristoteles die Induktion als Gewinnung von allgemeinen Aussagen aus der Betrachtung mehrerer Einzelfälle, und die Abduktion oder Apagoge gegenüber, die feststellt, dass bestimmte Einzelfälle unter eine gegelenge Entine noder noder.
Innerhalb der modernen Mathematischen Logik und allen formalen Systemen wird ein möglichst durchgehender Aufbau mit deduktiven Prinzipien angestrebt. Auch die Mathematik liegt weitgehend in deduktivem Aufbau vor und wird vorwiegend so gelehrt; d. час ihre Ergebnisse werden aus Axiomensystemen Formal abgeleitet. Deduktive Geschlossenheit ist ein wesentliches Merkmal formaler Beweise in der Mathematik. Die Mathematischen Verfahren der vollständigen Induktion und der transfiniten Induktion sind entgegen ihren Bezeichnungen deduktive Verfahren.
Der einfachste Fall der Anwendung der deduktiven Methode ist die Beseitigung einer Implikation mit Hilfe der Abtrennungsregel. Die logische Struktur dieser Regel ist die allgemeine Struktur eines Arguments, das aus einer Menge von Prämissen nach einer Schlussregel auf eine Konklusion schließt:
| п | (Prämisse 1) |
| p → q | (Prämisse 2) |
| ——— | |
| q | (Konklusion) |
Sind p und p → q (sprich: wenn p , dann q ) wahre Aussagen, so ist auch q eine wahre Aussage.
Entscheidbarkeit [Bearbeiten | Quelltext Bearbeiten]
Es gibt logische Systeme, in denen Ausdrücke auftreten, die zwar mit den Hilfsmitteln dieses Systems formuliert werden können, in ihm aber nicht entscheidbar sind. Deduktive und reduktive Schlussweisen werden in ihrer einfachen Struktur nur selten angewandt. Das tatsächlich wissenschaftliche Ableiten ist ein komplexes System von deduktiven, reduktiven und heuristischen Verfahren.
Die Auffassung, dass Deduktion und Induktion komplementäre Elemente der wissenschaftlichen Wahrheitsfindung sind, ist auch bestritten wordden, am prominentesten von Karl Popper.Ihm zufolge handelt es sich bei der Induktion nicht um ein Beweisverfahren. Allgemeine Regeln werden in Poppers Falsifikationismus nicht nach bestimmten индуктивен Regeln aus der Empirie hergeleitet, solche Regeln sind ihm zufolge предлагает Heuristiken für das Finden allgemeiner Hypothesen. Alle Schlüsse, die in der Wissenschaft gezogen werden, sind für ihn daher rein deduktiv, auch Schlüsse vom Besonderen auf das Allgemeine: Diese erfolgen im modus tollens, beispielsweise wenn eine allgemeine Theorpothesendorpothese.
In den Naturwissenschaften müssen durch Deduktion ermittelte Vorhersagen empirisch überprüfbar sein, um einen wissenschaftlichen Wert zu besitzen. Wenn die Beobachtungen nicht mit den Vorhersagen übereinstimmen, muss die Theorie angepasst oder verworfen werden.
Die deduktive Methode wird allgemein aber nicht für die einzige Methode der Gewinnung neuer wissenschaftlicher Erkenntnisse gehalten. Solch eine Methode muss stets von Prämissen ausgehen, die ihrerseits als wahr zu beweisen sind, hypothetisch als wahr vorausgesetzt werden oder axiomatisch als wahr gesetzt.Selbst wenn sich solche Prämissen wiederum aus anderen Prämissen deduktivableiten lassen, muss diese Beweiskette doch irgendwo beginnen (siehe: Infiniter Regress).
Die Wissenschaft muss zu Beweisverfahren greifen, die nicht-deduktiver Natur sind, denen alsotensionale Beziehungen zugrunde liegen. Es handelt sich dabei также um empirische Verfahren, welche Erkenntnisse durch Beobachtung und Experimente gewinnen. Die logische Verarbeitung der Ergebnisse der Praxis zu wissenschaftlichen Aussagen или Gar Gesetzen geschieht mit der reduktiven Methode .
Neben Logik, Philosophie und Linguistik beschäftigt sich auch die Denkpsychologie mit der menschlichen Kompetenz und Inkompetenz beim schlussfolgernden Denken. [1]
Als wichtigste Theorien sind zu nennen:
Die Psychologie untersucht, warum und wie Menschen überhaupt schlussfolgern können, warum sie dabei Fehler machen und welche Fehler häufiger gemacht werden als andere. Um Inhaltseffekte auszuschließen, hat man sich dabei meist syllogistischer Aufgaben bedient.Es zeigte sich, dass Menschen sehr häufig nicht official-logisch denken, sondern stattdessen, besonders unter Zeitdruck, Heuristiken benutzen. Dabei lassen sich systematische Fehler erkennen, die in der Fachliteratur auch als Bias (англ. Für Vorurteil, Befangenheit, Tendenz) или Kognitive Verzerrung bezeichnet werden. So werden unlogische, aber vom Inhalt her glaubwürdige Schlussfolgerungen oft für wahr gehalten, ebenso logisch valide, aber unglaubwürdige Konklusionen irrtümlich für falsch (sog.Вера-предубеждение). [2] Ebenfalls verbreitet ist die Tendenz, Schlussfolgerungen eher für wahr zu halten, die eigenen Überzeugungen bestätigen (sog. Bestätigungsfehler, англ. Смещение подтверждения).
- ↑ П. Джонсон-Лэрд, Р. Бирн: Удержание . Psychology Press, Хоув (Великобритания) 1991, ISBN 0-86377-148-3.
- ↑ Vgl. z. Б. Х. Марковиц / Г. Нантель: Эффект предубеждения и предвзятости при производстве и оценке логических выводов. В: Память и познание 17/1 (1989), 11–17.
.
определение дедукции The Free Dictionary
В этом направлении такой вывод бесспорен, как и вывод, сделанный Вольтером в шутку (не зная, над чем он шутит), когда он увидел, что резня святого Он обладает способностью наблюдения и умением делать выводы. Ему просто не хватает знаний; и это может произойти со временем. Как и все другие искусства, Наука Дедукции и Анализа может быть приобретена только путем долгого и терпеливого изучения, а жизнь не является достаточно продолжительной, чтобы позволить любому смертному достичь в ней наивысшего совершенства.Поэтому их можно было бы с большой долей уместности рассматривать как нечто большее, чем просто вывод из реальных представителей нации, ибо, подумал Ахав, даже в высших земных счастьях всегда таится некоторая ничтожная мелочность, но, по сути, все сердечные печали, мистическое значение, а у некоторых людей архангельское величие; поэтому их тщательные выкладки не противоречат очевидному выводу. Если проследить генеалогию этих высоких смертных страданий, мы, наконец, перенесемся среди не имеющих первоисточников первородных богов; так что перед лицом всех радостных соленых солнц и мягких звуков круглых лун урожая мы должны уступить этому: сами боги не вечно радуются.Мой свет горел до двух и трех часов ночи, что натолкнуло хорошую соседку на сентиментальную дедукцию Шерлока-Холмса. Не видя меня днем, она пришла к выводу, что я азартный игрок и что моя мать поместила туда свет в мое окно, чтобы вести ее заблудшего сына домой. Поэтому я говорю, что в совершенно несправедливом человеке мы должны предполагать самая совершенная несправедливость; здесь не должно быть никаких выводов, но мы должны позволить ему, совершая самые несправедливые поступки, снискать себе величайшую репутацию в качестве справедливого человека.Если мы уравновесим правильный вычет с одной стороны и тот, который, как предполагается, должен быть сделан с другой, пропорция все равно будет считаться верной. «Только то, что вы расстроили наши маленькие выводы. Вы говорите, ваш брак?» Но он никогда не связывал эти научные выводы о происхождении человека как животного, о рефлекторных действиях, биологии и социологии с теми вопросами о смысле жизни и смерти для него самого, которые в последнее время все больше и больше становятся предметом обсуждения. часто в его голове.Почему, конечно, законы природы, выводы естествознания, математика. Если я предпочитаю быть банальным, то это только для того, чтобы напомнить вам, что теории Коллиера сегодня столь же взорваны, как нелепые выводы испанской школы.
.
вычет существительное — определение, изображения, произношение и примечания по использованию
- [бесчисленное, исчисляемое] процесс использования информации, которая у вас есть, чтобы понять конкретную ситуацию или найти ответ на проблему
- Он пришел к решению путем простой процесс дедукции.
- Если мои выводы верны, я могу сказать вам, кто был убийцей.
- Мы можем исследовать кости динозавров и делать выводы о том, как они жили.
сравните индукцию (3) см. Также вывести Дополнительные примеры
- Она пришла к этому выводу путем логического вывода.
- детектив с отличными умениями
- Мы можем сделать некоторые выводы об истории руин.
Темы Математика и измеренияb2Oxford Collocations Dictionary прилагательное
- блестящий
- логический
- разумный
- …
глагол + вычитаниепредложение
- путем вычета
- вычет около
фраз См.
- умножение
- [неисчислимое, исчисляемое] процесс удаления некоторой суммы, особенно денег, из общей суммы; отнимаемая сумма
- Дивиденды будут выплачены без удержания налога.
- вычетов из вашей заработной платы налоговых и пенсионных взносов
- Компания автоматически производит налоговые вычеты из вашей заработной платы.
Дополнительные примеры
- отчисления на дорожные расходы
- ежемесячные отчисления на медицинское страхование
- Вы должны требовать удержания при подаче налоговой декларации.
Oxford Collocations Dictionary прилагательное глагол + дедукцияпредложение
- вычитание за
- вычет из
См. Полную запись
умножение
Степень вычитания
полная запись
Word Originlate среднеанглийский: от латинского deductio (n-), от глагола deducere, от de- ‘down’ + ducere ‘lead ‘.
См. Дедукцию в Oxford Advanced American Dictionary См. Дедукцию в Oxford Learner’s Dictionary of Academic English.
