Формы логики: Логические формы и их виды

Логические формы и их виды

    Содержание

Введение 3

1  Понятие 
логической формы   4

2. Логические 
формы 5

2.1 Понятие  5

2.2 Суждение  6

2.3 Умозаключение  10

Заключение 17

Библиографический
список  18 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

    Введение

    Логика
— философская наука, изучающая логические
формы человеческого мышления и 
законы, которым подчиняется мышление. 

    Логика 
изучает не конкретное содержание действительности,
а мысли о ней, их структуру, то,
что является общим для мыслей
данного типа, независимо от их конкретного 
содержания.  Поэтому при изучении
логики для того, чтобы понять сущность
процесса мышления, специфическое содержание
форм и законов, нужно уметь обобщать
конкретные рассуждения, уметь оперировать 
получаемыми формулами и схемами.
Основная цель изучения логики, сводится
к приобретению навыков осознанного 
применения логических правил и законов 
к реальному процессу  мышления.

    Знание 
логики позволяет анализировать 
рассуждения, помогает определить их последовательность,
непротиворечивость, доказательность,
и тем самым определять истинные
высказывания от ложных. Следовательно,
выбранная тема работы является весьма
актуальной на сегодняшний день.

    Целью
данной работы является изучение логических
форм и их видов.

    Для
достижения поставленной цели в работе
будут решены следующие задачи:

    1.
Дано понятие логической формы;

    2.
Рассмотрен логические формы. 
 
 
 
 
 
 
 
 

    1.
Понятие логической
формы

    Логический
строй мышления человека обладает очень
важным свойством — какую бы словесную
оболочку ни принимали наши мысли, на каком
бы языке ни излагались, они обязательно
должны принять общечеловеческие формы.
Без этого невозможно осуществить обмен
мыслями людей разных поколений и профессий,
а также взаимное понимание представителей
стран и народов.

    Выделяют 
три логические формы[3]:

    1.
Понятие;

    2.
Суждение;

    3.
Умозаключение.

    Логические
формы — это строение мысли, т.е. способ
связи её составных частей. В понятии —
это связь существенных признаков, в суждении
— связь понятий, в умозаключении — связь
суждений; а так же способ связи содержательных
частей рассуждения (доказательства, вывода
и т. п.). В соответствии с основным принципом
логики, правильность рассуждения зависит
только от его формы и не зависит от его
конкретного содержания. Само название
«формальная логика» подчеркивает, что
эта логика интересуется только формой
рассуждения. В реальном процессе мышления
содержание и форма мысли существуют в
неразрывном единстве. Нет «чистого»,
лишенного формы содержания, нет «чистых»,
бессодержательных логических форм. 
 
 
 
 
 
 
 

    2.
Логические формы

    2.1
Понятие 

    Понятие
— это отражение в сознании человека
общих и существенных свойств предмета
или явления. Понятие — это форма мышления,
в которой отражаются общие и притом существенные
свойства предметов и явлений[2]. Каждый
предмет, каждое явление имеют много различных
свойств, признаков. Эти свойства, признаки
можно разделить на две категории — существенные
и несущественные. Например, каждый отдельный
треугольник имеет три угла, определенные
размеры — длину сторон и площадь, определенную
величину углов, форму. Но только первый
признак делает фигуру треугольником,
позволяет отличить ее от других фигур:
прямоугольника, круга, трапеции. Остальные
признаки отличают один треугольник от
другого; при изменении их треугольник
не перестанет быть треугольником. Равно
и каждое отдельное дерево обладает и
такими признаками, которые позволяют
отличить его от кустарника, травы (т. е.
существенными признаками), например наличием
ствола, и такими, которые отличают одно
дерево от другого, например возраст, количество
ветвей, сохранность коры, наличие дупла
и т. д.

    Понятие
выступает и как форма мышления,
и как особое мыслительное действие.
За каждым понятием скрыто особое предметное
действие.

    Понятия
могут быть[1]:

• общими и
  единичными;
• конкретными
  и абстрактными;
• эмпирическими
  и теоретическими.

    Общее
понятие есть мысль, в которой 
отражаются общие, существенные и отличительные
(специфические) признаки предметов 
и явлений действительности. Единичное 
понятие есть мысль, в которой 
отражены присущие только отдельному
предмету и явлению признаки. В 
зависимости от типа абстракции и 
обобщений, лежащих в основе, понятия 
бывают эмпирическими или теоретическими.
Эмпирическое понятие фиксирует 
одинаковые предметы в каждом отдельном
классе предметов на основе сравнения.
Специфическим содержанием теоретического
понятия выступает объективная связь
всеобщего и единичного (целостного и
отличного). Понятия формируются в общественно-историческом
опыте. Человек усваивает систему понятий
в процессе жизни и деятельности.

    Каждое 
новое поколение людей усваивает 
научные, технические, моральные, эстетические
и другие понятия, выработанные обществом 
в процессе исторического развития.
Усвоить понятие — это значит осознать
его содержание, уметь выделять существенные
признаки, точно знать его границы
(объём), его место среди других
понятий с тем, чтобы не путать
со сходными понятиями; уметь пользоваться
данным понятием в познавательной и 
практической деятельности.

    Понятие
существует в виде значения слова, обозначается
словом. Каждое слово обобщает (кроме,
разумеется, слов, обозначающих имена 
собственные). В понятиях наши знания
о предметах и явлениях действительности
кристаллизуются в обобщенном и 
отвлеченном виде. В этом отношении 
понятие существенно отличается
от восприятия и представления памяти:
восприятие и представление конкретны,
образны, наглядны; понятие обладает
обобщенным, абстрактным, не наглядным 
характером.

    2.2
Суждение 

    Познавая 
объективный мир, человек раскрывает
связи между предметами и их признаками,
устанавливает отношения между 
предметами. Эти связи и отношения 
отражаются в мышлении в форме 
суждений, представляющих собой связь 
понятий.

    Связи
и отношения выражаются в суждении
посредством утверждения или 
отрицания. В суждении «Граждане РФ
имеют право на охрану здоровья» связь
между гражданами РФ и их правом на охрану
здоровья утверждается, а в суждении «Некоторые
преступления не являются умышленными»
связь между некоторой частью преступных
деяний и их умышленным характером отрицается.

    Всякое 
суждение может быть либо истинным,
либо ложным, т.е. соответствовать действительности
либо не соответствовать ей. Если в 
суждении утверждается связь, существующая
в действительности, или отрицается
связь, которая в действительности
отсутствует, то такое суждение будет 
истинным. Например, «Кража – преступление»,
«Астрология – не наука»– истинные суждения.
Если же в суждении утверждается связь,
которая в действительности не имеет места,
или отрицается действительно существующая
связь, то такое суждение является ложным.
Например, «Кража не является преступлением»,
«Астрология – наука»– ложные суждения,
они противоречат реальному положению
вещей, разъединяя то, что связано в действительности
(кражу и преступление), и связывая то,
что в действительности не связано (астрологию
и науку).

    Существуют 
суждения, истинность или ложность
которых очевидна или может быть
легко установлена (например, «Сегодня
солнечный день»или «Федоров – сотрудник
милиции»). Однако нередко она нуждается
в обосновании. Нельзя, например, признать
истинным суждение «Обвиняемый занимался
мошенничеством», пока виновность обвиняемого
в совершении данного преступления не
доказана[3].

    Истинность 
таких суждений нуждается в подтверждении 
с помощью других суждений, истинность
которых установлена.

    Итак,
суждение – это форма мышления,
в которой утверждается или отрицается
связь между предметом и его 
признаком или отношение между 
предметами и которая обладает свойством 
выражать либо истину, либо ложь.

    Языковой 
формой выражения суждения является
предложение. Подобно тому, как понятия 
не могут возникнуть и существовать
вне слов и словосочетаний, так 
и суждения не могут возникнуть и 
существовать вне предложений. Однако
единство суждения и предложения 
не означает их полного совпадения.
И если всякое суждение выражается
в предложении, то из этого не следует,
что всякое предложение выражает суждение.
Суждение выражается повествовательным
предложением, в котором содержится сообщение
о чем-либо.

    Кроме
повествовательных существуют вопросительные
и побудительные предложения, которые 
суждений не выражают

    Вопросительное 
предложение не выражает суждения,
так как его назначение состоит 
не в передаче информации, а в 
побуждении к ее получению. Побудительное 
предложение, выражающее волеизъявление,
направленное на осуществление определенных
действий, также не выражает суждения;
как и вопросительное предложение,
не утверждая и не отрицая чего-либо
о чем-либо, оно не может рассматриваться 
как истинное или ложное.

    Суждение 
о связи предмета и его признака
состоит из двух понятий – двух
терминов суждения: субъекта, отражающего 
предмет суждения, и предиката, отражающего 
признак предмета. Кроме субъекта и
предиката суждение включает в свой состав
связку – элемент суждения, который соединяет
оба термина суждения, утверждая или отрицая
принадлежность предмету некоторого признака.
Связка выражается словами «есть» («не
есть»), «является» («не является») и т.
п. В русском языке связка обычно подразумевается
или заменяется тире.

    В
распространенном предложении кроме 
главных членов – подлежащего 
и сказуемого – имеются второстепенные
члены (определение, дополнение, обстоятельство).
Например, в суждении «Национально-освободительное
движение охватило обширные районы бывшего
колониального и полуколониального мира»
субъектом является понятие «национально-освободительное
движение», в нем отражается предмет суждения;
понятие «охватило обширные районы бывшего
колониального и полуколониального мира»–
предикат суждения, отражающего то, что
утверждается о предмете суждения.

    В
отличие от подлежащего и сказуемого,
имеющих определенные грамматические
формы выражения, субъект и предикат
строго стабильных форм выражения не
имеют и нередко определяются
логическим ударением. Например, предложение 
«Степанов имеет высшее экономическое
образование» в зависимости от логического
ударения, с помощью которого выделяется
предикат суждения, может выражать три
разных суждения[4]:

• Степанов
  (а не кто-либо другой) имеет высшее экономическое
  образование;
• Степанов
  имеет высшее (а не среднее) экономическое
  образование;
• Степанов
  имеет высшее юридическое (а не какое-либо
  другое) образование.

    В
грамматически преобразованном 
виде эти суждения будут иметь 
следующий вид:

    1)
лицом, имеющим высшее экономическое
образование, является Степанов;

    2)
экономическое образование, которое имеет
Степанов, является высшим;

    З)
высшее образование, которое имеет 
Степанов, является экономическим.

    Различие 
между суждением и предложением
состоит также в том, что грамматический
строй предложения в разных языках
различен. Логическая же структура 
суждения одинакова независимо от его 
выражения в том или ином языке.

    Таким
образом, суждение и предложение 
образуют неразрывное единство, но
это единство включает в себя определенные
различия, которые необходимо учитывать,
так как отождествление суждения
как формы мышления и предложения 
как его языкового выражения 
порождает ошибки в рассуждениях. 

    В
логической литературе, наряду с термином
«суждение» употребляется термин «высказывание».
В символической логике (логике высказываний)
высказывания рассматриваются безотносительно
к их внутренней субъектно-предикатной
структуре.

    2.3
Умозаключение 

    Чтобы
уяснить происхождение и сущность
умозаключения, необходимо сопоставить 
два рода знаний, которыми мы располагаем 
и пользуемся в процессе своей 
жизнедеятельности, – непосредственные
и опосредованные[6]. Непосредственные
знания – это те, которые получены нами
с помощью органов чувств: зрения, слуха,
обоняния и т.д.

    Таковы,
например, знания, выраженные суждениями
типа «Дерево зеленое», «Снег бел», «Птица
поет», «Сосновый лес пахнет смолой». Они
составляют значительную часть всех наших
знаний и служат их базой.

Предмет логики. Основные логические формы

1. Предмет логики. Основные логические формы.

Логика происходит от греч. logos, что одновременно означает речь, слово, высказывание, понятие. Основатель логики Аристотель чаще всего употреблял термин «логос» в смысле «определения» или «разумности вообще».

Итак, в современном понимании, логика — это наука о законах и формах правильного мышления.

Форма мышления — это способ связи элементов мысли. Основные формы мышления (логические формы): понятие, суждение, умозаключение.

Понятие является исходной, самой простой формой мысли, отражая общие существенные признаки предметов.

Суждение — это форма мышления, в которой утверждается или отрицается связь между предметом и его признаком. Обладает свойством выражать либо истину (соответствие действительности), либо ложь.

Умозаключение — самая сложная форма мысли, представляет собой получение нового суждения (вывода) из данных суждений (посылок).

Логика, как отдельная наука впервые была систематически изложена древнегреческим философом Аристотелем (384 — 322 гг. до н. э.). Аристотель сформулировал основные законы правильного мышления: закон тождества, закон непротиворечия, закон исключенного третьего. Позднее был сформулирован четвертый закон — закон достаточного основания. Разработка логики во многом была обусловлена общественной потребностью. Гражданин античного полиса активно участвовал в общественной жизни. Свободнорожденный мужчина, хотя бы раз в жизни должен был занимать важный государственный пост. Это требовало определенной подготовки. Поэтому высоко ценились так называемы «учителя мудрости» — софисты. Они учили грамоте, красноречию, искусству спора и т. д., однако со временем стали изобретать приемы одурачивания собеседника. Такие недобросовестные приемы получили название «софизмов», а слово «софист» приобрело негативный смысл.

Вот примеры некоторых софизмов, ставших классическими:

«То, что ты не потерял, то у тебя есть. Ты не терял рогов. Значит, они у тебя есть (ты рогат)»;
«Сидящий встал. Кто встал, тот стоит. Значит, сидящий стоит»;
«Я — человек. Вы не я. Значит, вы не человек»;
«Лекарство для больного — это добро. Чем больше добра тем лучше. Значит чем больше ты дашь лекарства больному, тем лучше».

А вот вопросы софистского толка:

«Перестал ли ты бить свою мать?»;
«Давно ли ты вышел из тюрьмы?» и т. п.

Очевидно, что любой ответ на такой вопрос вас не устроит.Ввязываясь, например, в такой спор, «спорим, что я трактор поднимал?» вы заранее обрекает себя на проигрыш («поднимал, но не поднял» или «поднимал, но игрушечный»). Так же как отвечая на такие вопросы:

«- Знаете ли вы, о чем я хочу вас сейчас спросить?- Нет, не знаем.- Неужели вы не знаете, что лгать — нехорошо?- Знаем.- Но именно об этом я и собирался вас спросить, а вы ответили, что не знаете. Выходит вы знаете то, чего не знаете!»

Двусмысленность многих языковых выражений, скрытые утверждения в вопросах, все это позволяет софизму выглядеть убедительным для неподготовленного человека. Умение пользоваться софизмами предполагает знание основ логики.

Именно как средство защиты от софистики и лжи логика и была задумана Аристотелем. В дальнейшем значительный вклад в разработку логики внесли средневековые схоласты (ввели латинскую терминологию). Английский философ Ф. Бэкон (1561-1626) заложил основы учения об индуктивных умозаключениях. Немецкий философ Лейбниц (1646-1716) сформулировал закон достаточного основания. В середине XIX в. возникла математическая (символическая) логика. С тех пор аристотелевская логика стала называться традиционной (формальной) логикой.

2. Законы логики.

3. Значение логики.

Достижения формальной логики применяются в юриспруденции, психологии, лингвистике, теории управления, педагогике и др. науках. Некоторые разделы логики являются теоретической основой математики, теории информации, кибернетики.

При изучении логики развиваются:

1. точное мышление и ясная речь;
2. умение убеждать и обосновывать свои идеи;
3. умение спорить;
4. привычка анализировать свои и чужие рассуждения, что помогает нам справиться с софистикой и ложью.

Но все же главное значение логики в том, что она приучает думать и усиливает мыслительные способности человека.

Следователь – следователь прокуратуры

Конституция – закон

Общество – человек

Стихотворный размер – Стихотворный размер ямб

6. Три примера дедуктивных умозаключений:

Если день солнечный, то сосновый лес пахнет смолой.
День — солнечный.
____________________
Следовательно, сосновый лес пахнет смолой.

2. Все звезды излучают энергию

Солнце – это звезда.

_________________________________________________
Следовательно, Солнце излучает энергию.

3. Если решение суда обжаловано в апелляционном порядке, то оно еще не вступило в законную силу.
Решение суда обжаловано в апелляционном порядке.
_____________________________________________
Следовательно, оно еще не вступило в законную силу.

Шпаргалка логическое мышление и его формы

Мышление в отличие от других процессов совершается в соответствии с определенной логикой.

В структуре мышления можно выделить следующие логические операции:

• сравнение;
• анализ;
• синтез;
• абстрагирование;
• обобщение.

Сравнение — мыслительная операции, основанная на установлении сходства и различия между объектами. Результатом сравнения может стать классификация, которая выступает как первичная форма теоретического познания.

Анализ — мыслительная операция расчленения сложного объекта на составляющие его части или характеристики с последующим их сравнением.

Синтез — операция, обратная анализу, позволяющая мысленно воссоздать целое из аналитически заданных частей. Анализ и синтез обычно осуществляются вместе, способствуя более глубокому познанию действительности.

Абстрагирование — мыслительная операция, основанная на выделении существенных свойств и связей предмета и отвлечении от других, несущественных. Эти выделенные характеристики как самостоятельные предметы в действительности не существуют. Абстрагирование способствует более тщательному их изучению. Результатом абстрагирования выступает формирование понятий.

Обобщение — мысленное объединение предметов и явлений по их общим и существенным признакам.

Формы логического мышления

Основными формами логического мышления являются:

• понятия;
• суждения;
• умозаключения.

Понятие

Понятие — форма мышления, отражающая существенные свойства, связи и отношения предметов и явлений, выраженная словом или группой слов. Понятия могут быть конкретными и абстрактными.

Суждение

Суждение — форма мышления, отражающая связи между предметами и явлениями в форме утверждения илиотрицания. Суждения могут быть истинными или ложными.

Умозаключение

Умозаключение — форма мышления, при которой на основе нескольких суждений делается определенный вывод.

Различаются умозаключения:

• индуктивные;
• дедуктивные;
• по аналогии.

Индукция — логический вывод в процессе мышления от частного к общему.

Дедукция — логический вывод в процессе мышления от общего к частному.

Аналогия — логический вывод в процессе мышления от частного к частному на основе некоторых элементов сходства.

Хотя мышление осуществляется на основе логических операций, оно не всегда выступает как процесс, в котором действуют только логика и разум. В процесс мышления очень часто вмешиваются, изменяя его, эмоции. Эмоции подчиняют мысль чувству, заставляя подбирать доводы, говорящие в пользу желаемого решения.

Эмоции способны не только искажать, но и стимулировать мышление. Известно, что чувство придаст мышлению напряженность, остроту, целеустремленность и настойчивость. Как утверждает психология, без возвышенного чувства продуктивная мысль столь же невозможна, как без логики, знаний, умений, навыков.

Логика и эмоции в процессе мышления

Мышление в отличие от других процессов совершается в соответствии с определенной логикой. В структуре мышления можно выделить следующие логические операции: сравнение, анализ, синтез. абстрагирование и обобщение.

Сравнение — мыслительная операция, основанная на установлении сходства и различия между объектами. Результатом сравнения может стать классификация, которая выступает как первичная форма теоретического познания.

Анализ — мыслительная операция расчленения сложного объекта на составляющие его части или характеристики с последующим их сравнением.

Синтез — операция, обратная анализу, позволяющая мысленно воссоздать целое из аналитически заданных частей. Анализ и синтез обычно осуществляются вместе, способствуя более глубокому Познанию действительности.

Абстрагирование — мыслительная операция, основанная на вы делении существенных свойств и связей предмета и отвлечении от других, несущественных. Эти выделенные характеристики как самостоятельные предметы в действительности не существуют. Абстрагирование способствует более тщательному их изучению. Результатом абстрагирования выступает формирование понятий.

Обобщение — мысленное объединение предметов и явлении по их общим и существенным признакам.

Основными формами логического мышления являются понятия, суждения и умозаключения.

Понятие — форма мышления, отражающая существенные свойства, связи и отношения предметов и явлений, выраженная словом или группой слов. Понятия могут быть конкретными и абстрактными.

Суждение — форма мышления, отражающая связи между предметами и явлениями в форме утверждения илиотрицания. Суждения могут быть истинными или ложными.

Умозаключение — форма мышления, при которой на основе нескольких суждений делается определенный вывод.Различаются умозаключения индуктивные, дедуктивные и по аналогии.

Индукция — логический вывод в процессе мышления от частного к общему. Дедукция — логический вывод в процессе мышления от общего к частному.

Аналогия — логический вывод в процессе мышления от частного к частному на основе некоторых элементов сходства.

Хотя мышление осуществляется на основе логических операций, оно не всегда выступает как процесс, в котором действуют только логика и разум. В процесс мышления очень часто вмешиваются, изменяя его, эмоции. Эмоции подчиняют мысль чувству, заставляя подбирать доводы, говорящие в пользу желаемого решения.

Эмоции способны не только искажать, но и стимулировать мышление. Известно, что чувство придает мышлению напряженность, остроту, целеустремленность и настойчивость. Как утверждает психология, без возвышенного чувства продуктивная мысль столь же невозможна, как без логики, знаний, умений, навыков.

ЛОГИЧЕСКАЯ ФОРМА – Словарь по логике, А.А. Ивин, А.Л. Никифоров

А.А. Ивин, А.Л. Никифоров

– способ связи содержательных частей рассуждения (доказательства, вывода и т. п.). В соответствии с основным принципом логики, правильность рассуждения зависит только от его формы и не зависит от его конкретного содержания. Само название «формальная логика» подчеркивает, что эта логика интересуется только формой рассуждения. Л. ф. представляется посредством логических констант и переменных. Логические константы, подобные «и», «или», «если, то» и т. д., не имеют самостоятельного содержания, но с их помощью из одних содержательных выражений могут быть получены новые содержательные выражения. Переменные, входящие в Л. ф., представляют выражения, обладающие самостоятельным содержанием: высказывания, имена (см.: Символы собственные и несобственные).

Напр., высказывания «Все лошади едят овес» и «Все реки впадают в море» различны по своему содержанию, причем первое истинно, а второе ложно. Отвлекаясь от содержания высказываний, можно заменить их части переменными S и Р. Получим, что данные высказывания имеют одну и ту же логическую форму: «Все S есть Р». Содержательно разные высказывания «Если есть огонь, то есть дым» и «Если математика – наука, то она устанавливает законы» также имеют одинаковую логическую форму: «Если А, то В».

Следующие два вывода, различающиеся своим содержанием, совпадают по своей логической форме: «Если сейчас день, то светло. Сейчас день. Следовательно, светло» и «Если 13 – простое число, оно делится только на себя и на единицу. 13 – простое число. Следовательно, 13 делится только на себя на и на единицу». Заменив высказывания, входящие в данные выводы, переменными, получаем, что в обоих случаях рассуждение идет по одной и той же схеме: «Если А, то В. А. Следовательно, В». Это – схема правильного рассуждения: какие бы конкретные высказывания ни подставлялись вместо A и В, если посылки истинны, заключение также будет истинным (см.: Логическая правильность).

Различие между Л. ф. и содержанием не является абсолютным. То, что в одном случае считается относящимся к форме, в другом может оказаться содержательным компонентом рассуждения, и наоборот.

Интерес логики к Л. ф. не означает отвлечение ее от всякого содержания. Сама Л. ф. обладает определенным абстрактным содержанием, его иногда называют «формальным», чтобы отличить от «конкретного содержания». Скажем, форма «Все S есть Р» указывает, что у всякого предмета, обозначаемого буквой S, есть признак, обозначаемый буквой Р.

Понятие Л. ф. является центральным в логике. С ним связаны понятия логического закона, правила вывода, логического следования и др.

логическая форма — это… Что такое логическая форма?

— способ связи содержательных частей рассуждения (доказательства, вывода и т. п.). В соответствии с основным принципом логики, правильность рассуждения зависит только от его формы и не зависит от его конкретного содержания. Само название «формальная логика» подчеркивает, что эта логика интересуется только формой рассуждения. Л. ф. представляется посредством логических констант и переменных. Логические константы, подобные «и», «или», «если, то» и т. д., не имеют самостоятельного содержания, но с их помощью из одних содержательных выражений могут быть получены новые содержательные выражения. Переменные, входящие в Л. ф., представляют выражения, обладающие самостоятельным содержанием: высказывания, имена (см.: Символы собственные и несобственные).

Напр., высказывания «Все лошади едят овес» и «Все реки впадают в море» различны по своему содержанию, причем первое истинно, а второе ложно.

Отвлекаясь от содержания высказыва-

ний, можно заменить их части переменными S и Р. Получим, что данные высказывания имеют одну и ту же логическую форму: «Все S есть Р». Содержательно разные высказывания «Если есть огонь, то есть дым» и «Если математика — наука, то она устанавливает законы» также имеют одинаковую логическую форму: «Если А, то В».

Следующие два вывода, различающиеся своим содержанием, совпадают по своей логической форме: «Если сейчас день, то светло. Сейчас день. Следовательно, светло» и «Если 13 — простое число, оно делится только на себя и на единицу. 13 — простое число. Следовательно, 13 делится только на себя на и на единицу». Заменив высказывания, входящие в данные выводы, переменными, получаем, что в обоих случаях рассуждение идет по одной и той же схеме: «Если А, то В. А. Следовательно, В». Это — схема правильного рассуждения: какие бы конкретные высказывания ни подставлялись вместо A и В, если посылки истинны, заключение также будет истинным (см.: Логическая правильность).

Различие между Л. ф. и содержанием не является абсолютным. То, что в одном случае считается относящимся к форме, в другом может оказаться содержательным компонентом рассуждения, и наоборот.

Интерес логики к Л. ф. не означает отвлечение ее от всякого содержания. Сама Л. ф. обладает определенным абстрактным содержанием, его иногда называют «формальным», чтобы отличить от «конкретного содержания». Скажем, форма «Все S есть Р» указывает, что у всякого предмета, обозначаемого буквой S, есть признак, обозначаемый буквой Р.

Понятие Л. ф. является центральным в логике. С ним связаны понятия логического закона, правила вывода, логического следования и др.

Словарь по логике. — М.: Туманит, изд. центр ВЛАДОС.
А.А.Ивин, А.Л.Никифоров.
1997.

Логическая форма — Гуманитарный портал

Логика

%PDF-1.6 %
789 0 obj > endobj 863 0 obj >stream
2007-07-23T23:48:592019-07-16T10:17:44+03:002019-07-16T10:17:44+03:00ABBYY FineReader 8.0 Professional Editionapplication/pdf

uuid:6f60ee81-07e3-46cb-b002-b267d015a4d1uuid:56703390-dd1c-4785-9388-8a22e9d0f856

endstream endobj 790 0 obj > endobj 791 0 obj > endobj 1 0 obj > endobj 5 0 obj > endobj 9 0 obj > endobj 17 0 obj > endobj 21 0 obj > endobj 29 0 obj > endobj 35 0 obj > endobj 39 0 obj > endobj 43 0 obj > endobj 47 0 obj > endobj 53 0 obj > endobj 59 0 obj > endobj 63 0 obj > endobj 67 0 obj > endobj 71 0 obj > endobj 75 0 obj > endobj 79 0 obj > endobj 83 0 obj > endobj 87 0 obj > endobj 93 0 obj > endobj 97 0 obj > endobj 101 0 obj > endobj 105 0 obj > endobj 109 0 obj > endobj 113 0 obj > endobj 117 0 obj > endobj 121 0 obj > endobj 125 0 obj > endobj 129 0 obj > endobj 133 0 obj > endobj 141 0 obj > endobj 147 0 obj > endobj 155 0 obj > endobj 161 0 obj > endobj 167 0 obj > endobj 171 0 obj > endobj 175 0 obj > endobj 179 0 obj > endobj 183 0 obj > endobj 187 0 obj > endobj 191 0 obj > endobj 195 0 obj > endobj 199 0 obj > endobj 205 0 obj > endobj 209 0 obj > endobj 213 0 obj > endobj 217 0 obj > endobj 221 0 obj > endobj 227 0 obj > endobj 231 0 obj > endobj 235 0 obj > endobj 239 0 obj > endobj 243 0 obj > endobj 247 0 obj > endobj 251 0 obj > endobj 255 0 obj > endobj 259 0 obj > endobj 263 0 obj > endobj 267 0 obj > endobj 271 0 obj > endobj 275 0 obj > endobj 279 0 obj > endobj 283 0 obj > endobj 287 0 obj > endobj 291 0 obj > endobj 297 0 obj > endobj 301 0 obj > endobj 307 0 obj > endobj 313 0 obj > endobj 319 0 obj > endobj 325 0 obj > endobj 329 0 obj > endobj 333 0 obj > endobj 337 0 obj > endobj 341 0 obj > endobj 347 0 obj > endobj 353 0 obj > endobj 357 0 obj > endobj 361 0 obj > endobj 365 0 obj > endobj 369 0 obj > endobj 373 0 obj > endobj 377 0 obj > endobj 381 0 obj > endobj 387 0 obj > endobj 393 0 obj > endobj 397 0 obj > endobj 401 0 obj > endobj 405 0 obj > endobj 409 0 obj > endobj 413 0 obj > endobj 417 0 obj > endobj 421 0 obj > endobj 425 0 obj > endobj 429 0 obj > endobj 433 0 obj > endobj 437 0 obj > endobj 441 0 obj > endobj 445 0 obj > endobj 449 0 obj > endobj 455 0 obj > endobj 459 0 obj > endobj 463 0 obj > endobj 467 0 obj > endobj 473 0 obj > endobj 477 0 obj > endobj 481 0 obj > endobj 485 0 obj > endobj 491 0 obj > endobj 495 0 obj > endobj 501 0 obj > endobj 505 0 obj > endobj 511 0 obj > endobj 517 0 obj > endobj 521 0 obj > endobj 525 0 obj > endobj 529 0 obj > endobj 533 0 obj > endobj 537 0 obj > endobj 541 0 obj > endobj 545 0 obj > endobj 549 0 obj > endobj 553 0 obj > endobj 557 0 obj > endobj 563 0 obj > endobj 569 0 obj > endobj 573 0 obj > endobj 577 0 obj > endobj 581 0 obj > endobj 585 0 obj > endobj 589 0 obj > endobj 593 0 obj > endobj 597 0 obj > endobj 601 0 obj > endobj 605 0 obj > endobj 609 0 obj > endobj 613 0 obj > endobj 617 0 obj > endobj 623 0 obj > endobj 629 0 obj > endobj 633 0 obj > endobj 637 0 obj > endobj 643 0 obj > endobj 649 0 obj > endobj 653 0 obj > endobj 659 0 obj > endobj 665 0 obj > endobj 669 0 obj > endobj 673 0 obj > endobj 677 0 obj > endobj 681 0 obj > endobj 685 0 obj > endobj 689 0 obj > endobj 693 0 obj > endobj 697 0 obj > endobj 701 0 obj > endobj 705 0 obj > endobj 709 0 obj > endobj 713 0 obj > endobj 717 0 obj > endobj 721 0 obj > endobj 725 0 obj > endobj 729 0 obj > endobj 733 0 obj > endobj 737 0 obj > endobj 741 0 obj > endobj 745 0 obj > endobj 749 0 obj > endobj 753 0 obj > endobj 757 0 obj > endobj 761 0 obj > endobj 767 0 obj > endobj 771 0 obj > endobj 775 0 obj > endobj 781 0 obj > endobj 783 0 obj >stream
xWn#EC/3S[[HDrv#!!4A)3(ᱤIcvTף]v yѭS9U|(FpmRibt>*FMFP$Fa\

Примеры логики

Проще говоря, логика — это «изучение правильных рассуждений, особенно в отношении умозаключений». Логика зародилась как философский термин и теперь используется в других дисциплинах, таких как математика и информатика. Хотя определение кажется достаточно простым, понимание логики немного сложнее. Используйте примеры логики, чтобы научиться правильно использовать логику.

Пример формальной логики

Определения логики

Логика может включать в себя рассуждение людей с целью формирования мыслей и мнений, а также классификации и суждений.Некоторые формы логики также могут выполняться компьютерами и даже животными.

Логика может быть определена как:

«Изучение истин, полностью основанное на значениях содержащихся в них терминов».

Логика — это процесс вывода и инструмент, который вы можете использовать.

• Основанием логического аргумента является его предложение или утверждение.

• Утверждение либо верно (верно), либо нет (ложно).

• Предпосылки — это суждения, используемые для построения аргумента.

• Аргумент затем строится локально.

• Затем вывод делается из помещений.

• Наконец, делается вывод .

Определение логики в философии

Логика — это раздел философии. Существуют разные школы мысли о логике в философии, но типичная версия называется классической элементарной логикой или классической логикой первого порядка .В этой дисциплине философы пытаются отличить хорошее рассуждение от плохого.

Определение логики в математике

Логика также является областью математики. Математическая логика использует пропозициональных переменных , которые часто представляют собой буквы, для представления пропозиций .

Типы логики с примерами

Вообще говоря, существует четыре типа логики.

Неформальная логика

Неформальная логика — это то, что обычно используется в повседневных рассуждениях.Это рассуждения и аргументы, которые вы приводите в личном общении с другими.

• Помещение: Никки увидела черную кошку, шедшую на работу. На работе Никки уволили.

  Заключение: Черные кошки — несчастье.

  Объяснение: Это большое обобщение, которое невозможно проверить.

• Помещение: нет доказательств того, что пенициллин вреден для вас. Пенициллин использую без проблем.

  Вывод: пенициллин безопасен для всех.

  Объяснение: Личный опыт или недостаток знаний не поддаются проверке.

• Помещение: Моя мама — знаменитость. Я живу с мамой.

  Вывод: я знаменитость.

  Объяснение: Доказательство славы — это нечто большее, чем если бы она стерлась.

Формальная логика

В формальной логике вы используете дедуктивное рассуждение, и посылки должны быть верными. Вы следуете предпосылкам, чтобы прийти к формальному выводу.

• Помещение: каждый человек, живущий в Квебеке, живет в Канаде. Все в Канаде живут в Северной Америке.

  Заключение: Каждый человек, живущий в Квебеке, живет в Северной Америке.

  Пояснение: Здесь представлены только достоверные факты.

• Помещения: У всех пауков восемь ног. Черные вдовы — разновидность пауков.

  Заключение: у черных вдов восемь ног.

  Объяснение: Этот аргумент не является спорным.

• Помещения: Велосипеды двухколесные. Ян катается на велосипеде.

  Вывод: Ян едет на двух колесах.

  Объяснение: Посылки верны, и заключение тоже.

Символьная логика

Символьная логика определяет, как символы соотносятся друг с другом. Он присваивает символы вербальным рассуждениям, чтобы иметь возможность проверить достоверность утверждений с помощью математического процесса. Обычно такой тип логики используется в расчетах.

Пример символической логики:

• Утверждения: Если все млекопитающие кормят своих детей молоком матери (A). Если все кошки кормят своих малышей материнским молоком (B). Все кошки — млекопитающие (С). Знак Ʌ означает «и», а символ ⇒ означает «подразумевает».

• Заключение: A Ʌ B ⇒ C

• Объяснение: Предложение A и предложение B приводят к выводу C. Если все млекопитающие кормят своих детей молоком матери, а все кошки кормят своих детей материнским молоком, это подразумевает все кошки — млекопитающие.

Математическая логика

В математической логике вы применяете формальную логику к математике. Этот тип логики является частью основы логики, используемой в компьютерных науках. Математическая логика и символическая логика часто используются как синонимы.

Типы рассуждений с примерами

Каждый тип логики может включать дедуктивное рассуждение, индуктивное рассуждение или и то, и другое.

Примеры дедуктивного мышления

Дедуктивное рассуждение обеспечивает полное доказательство истинности своего вывода.Он использует конкретную и точную предпосылку, которая приводит к конкретному и точному выводу. При правильных предпосылках вывод такого рода аргументов поддается проверке и является правильным.

• Помещение: Все квадраты прямоугольные. У всех прямоугольников четыре стороны.

  Вывод: у всех квадратов четыре стороны.

• Помещение: Все люди смертны. Ты человек.

  Заключение: Вы смертны.

• Помещение: У всех деревьев есть стволы.Дуб — это дерево.

  Заключение: У дуба есть ствол.

Примеры индуктивной логики

Индуктивное рассуждение работает «снизу вверх», что означает, что оно берет конкретную информацию и делает широкое обобщение, которое считается вероятным, учитывая тот факт, что вывод может быть неточным. Этот тип рассуждений обычно включает в себя правило, устанавливаемое на основе серии повторяющихся опытов.

• Помещение: Зонт предохраняет от промокания под дождем.Эшли взяла свой зонтик, и она не промокла.

  Заключение: в этом случае вы можете использовать индуктивное рассуждение, чтобы высказать мнение, что, вероятно, идет дождь.

  Пояснение: Ваше заключение, однако, не обязательно будет точным, потому что Эшли осталась бы сухой независимо от того, идет ли дождь и у нее был зонтик, или он не шел вообще.

• Помещения: Каждый трехлетний ребенок, которого вы видите в парке каждый день, проводит большую часть своего времени в слезах и криках.

  Заключение: все трехлетние дети должны проводить день в криках.

  Объяснение: Это не обязательно будет правильным, потому что вы не видели каждого трехлетнего ребенка в мире днем, чтобы проверить это.

• Помещения: сгорело двенадцать из 20 домов квартала. Каждый пожар был вызван неисправной проводкой.

  Заключение: Если более чем в половине домов неисправна проводка, значит, во всех домах в квартале неисправна проводка.

  Объяснение: Вы не знаете, что это заключение достоверно, но вероятно.

• Помещение: Красный свет предотвращает несчастные случаи. Майк сегодня за рулем не попал в аварию.

  Вывод: Майк, должно быть, остановился на красный свет.

  Объяснение: Майк мог вообще не встретить никаких светофоров. Следовательно, он мог бы избежать несчастных случаев, даже не останавливаясь на красный свет.

Следуйте логике

Как показывают эти примеры, вы можете использовать логику для решения проблем и делать выводы.Иногда эти выводы являются правильными, а иногда неточными. Когда вы используете дедуктивное рассуждение, вы приходите к правильным логическим аргументам, в то время как индуктивное рассуждение может дать или не дать вам правильный результат. Ознакомьтесь с примерами логических ошибок, чтобы увидеть, как выглядят неправильные логические рассуждения.

Собака, нюхающая под одеялом, как пример логики.

Условная логика и ветвление форм | 123FormBuilder Блог

Условная логика везде. Вы найдете это в грамматике, вы увидите это в программировании, и да, вы можете не удивиться этому (учитывая то, что мы делаем), вы также найдете это в формах.

Формы условной логики намного увлекательнее и интереснее, чем некоторые думают. То, что условная логика может сделать с вашими формами, почти волшебно: она может преобразовывать их в персонализированные рабочие процессы, позволяя пользователям вашего сайта получать доступ к различным разделам на основе их ответов.

Отлично, правда?

Давайте глубже погрузимся в формы условной логики, логику форм и все, что поможет вам создавать формы, соответствующие вашему поведению пользователя.

Что такое условная логика?

Условная логика опирается на условные утверждения (более известные как предложения if в теории грамматики).

Если я перееду тесто, я поправлюсь.

Форма моего тела и вес, таким образом, являются логическим следствием моей привычки к выпечке.

Если вы выйдете под дождь, то простудитесь.

Если бы люди могли жить на Марсе, на Земле было бы больше места.

Вы уловили суть — если вы строите предложение, основанное на парадигме «если-то», то это означает, что вы используете условную логику. Таким образом, определение условной логики может быть таким простым, как «ветвь логики, основанная на предложениях« если … то ».

Конечно, мы могли бы написать целую книгу о чудесах и красотах условной логики, но мы здесь, чтобы проиллюстрировать и показать вам, как создавать умные формы с использованием условной логики.

Что такое условная логическая форма?

Проще говоря, форма с условной логикой — это веб-форма, в которой используется условная логика для создания персонализированного взаимодействия с пользователем.

Эта идея может показаться не такой уж большой, но у нее есть несколько удивительных преимуществ, включая (но не только):

• Сохраняйте форму короткой, приятной и нескучной
• Позволяет создавать личные впечатления для пользователей в мире, который на данный момент довольно единообразен.
• Перенаправить пользователей на определенную страницу (например,g., целевая страница, предназначенная для продажи конкретному пользователю)
• Создавайте веселые викторины (например, для привлечения людей на целевую страницу)
• Создавайте опросы и предоставляйте персональные ответы в соответствии с ответами пользователей

Список можно продолжать и продолжать.

По сути, когда вы научитесь трюку с условными формами, ваше творчество станет единственным пределом, который у вас есть.

Что такое условное поле?

В искусстве создания форм (потому что да, это так!) Условное поле — это поле формы, которое скрыто от пользователя, но будет разворачиваться в зависимости от его поведения.Если их поведение не соответствует назначению условного поля, форма совершит логический переход и переключится на следующее, наиболее подходящее поле.

Круто, правда?

Кстати, наш конструктор условных форм может помочь вам создавать условные поля и формы наиболее естественным и интуитивно понятным способом (подмигнуть, подмигнуть).

Как создавать формы с помощью условной логики

Вероятно, было бы бесполезно говорить, что у нас есть конструктор форм с условной логикой, но вот он: он у нас есть, и его легко использовать (даже я мог бы его использовать!).Наши формы условной логики работают в WordPress и практически на любой другой платформе CMS, о которой вы можете подумать (Woocommerce, Shopify, Wix — вы называете это).

Независимо от того, решите ли вы создавать условные формы WordPress или выберете другие платформы для демонстрации своих форм, основы остаются теми же:

• Вам нужно знать, что такое логическая форма
• Вам необходимо знать основные типы правил условной логики, применимые к формам
• Вам необходимо понять, как использовать построитель условных форм

Мы уже рассмотрели первый пункт, а затем обратимся к двум другим.

По сути, существует три основных типа правил, которые вы можете использовать при построении форм: правила формы, правила полей и правила автоответчика.

Ради логики (хех), давайте рассмотрим каждый из них один за другим:

1. Правила формы. Как следует из названия, эти правила можно применить ко всей форме. В общем, вам нужен этот тип правила, когда вы хотите отправить пользователей на другую страницу (например, страницу, которая предлагает им более подробную информацию о продукте, который лучше всего для них, в соответствии с анкетой, которую они только что заполнили).
2. Полевые правила. Опять же, название говорит само за себя: эти правила применяются к полям, когда вы хотите их скрыть (или показать), когда пользователи выполняют определенные действия в форме (например, если кто-то выбирает «мороженое» из меню «десерт» , вы можете установить правило для отображения меню «мороженое»).
3. Правила автоответчика. Эти правила похожи на правила форм, но вместо перенаправления пользователя на другую страницу или веб-сайт они отправят им автоматическое электронное письмо (например, когда кто-то подписывается на ваш информационный бюллетень, вы можете захотеть отправить ему благодарность и подтверждение по электронной почте — при условии, что у вас есть их согласие, конечно, согласно GDPR of).

Короче вот оно. Как только вы освоите эти правила, мир станет вашей игровой площадкой!

Как использовать 123FormBuilder для создания форм с условным ветвлением

Хорошо, теперь самое интересное: как использовать умный конструктор форм 123FormBuilder для создания формы с условной логикой?

Итак, вы создаете свою онлайн-форму, как обычно, и применяете правило, которое соответствует вашим потребностям, а именно:

1. Зарегистрируйтесь или войдите в 123FormBuilder
2. Создайте форму
3. Щелкните вкладку Настройки
4. Перейти к правилам
5. На горизонтальной ленте выберите тип правила, которое вы хотите использовать (в соответствии с описанием, которое мы сделали в предыдущем разделе этой статьи): правила формы, правила поля или правила автоответчика.Узнайте больше об использовании этой функции в нашем руководстве по условной логике.

Вот несколько их скриншотов во всей красе и красоте:

Правила формы

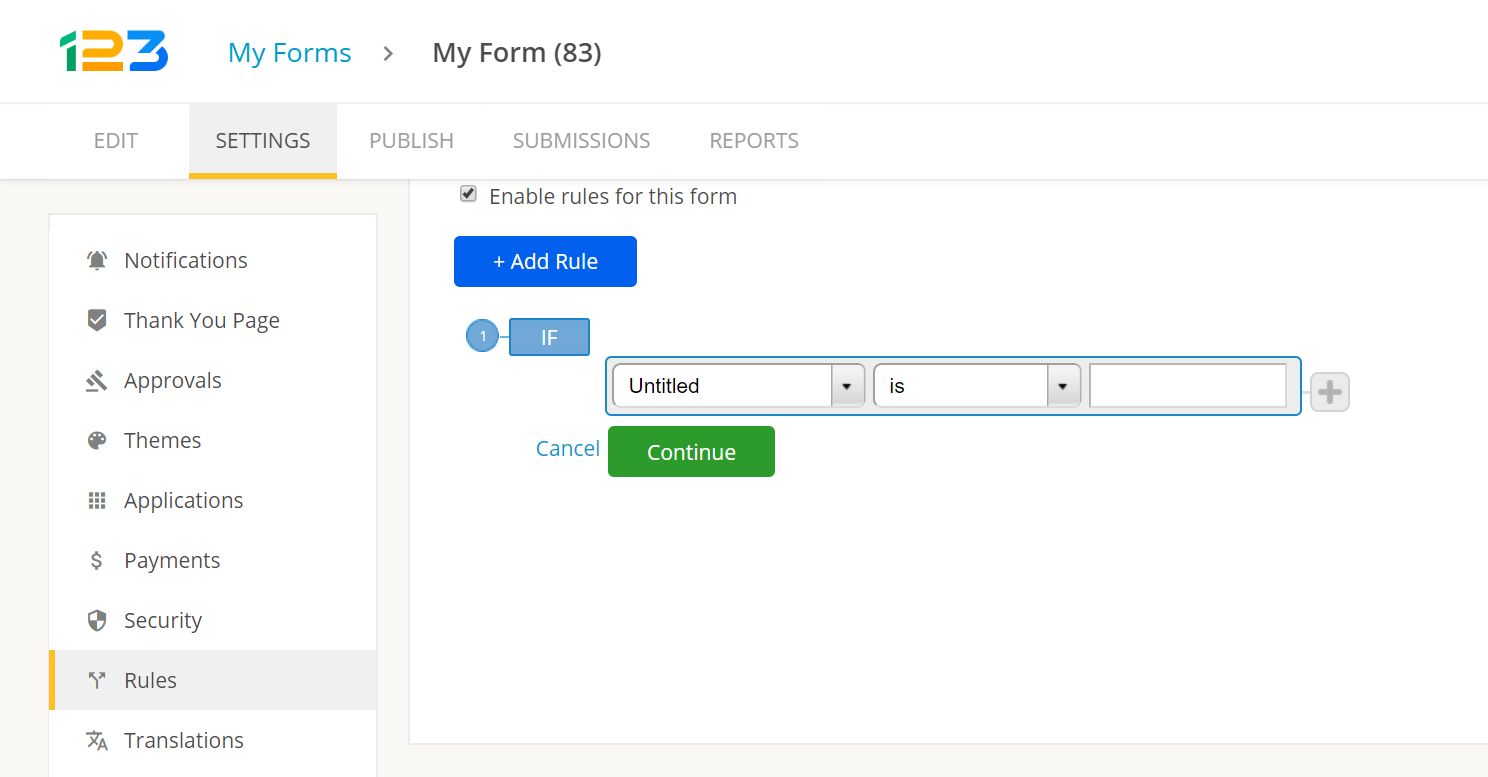
Полевые правила

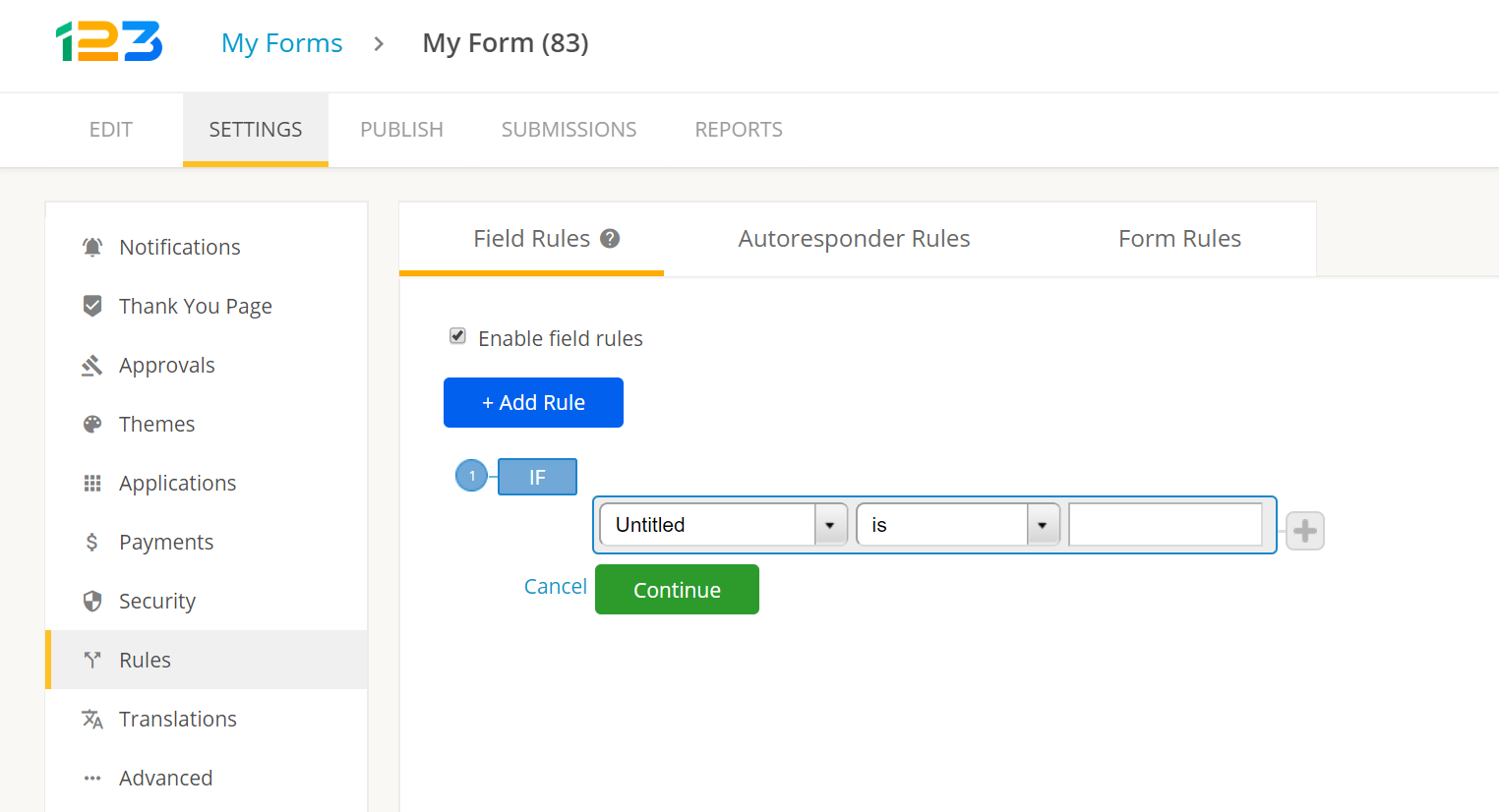
Правила автоответчика

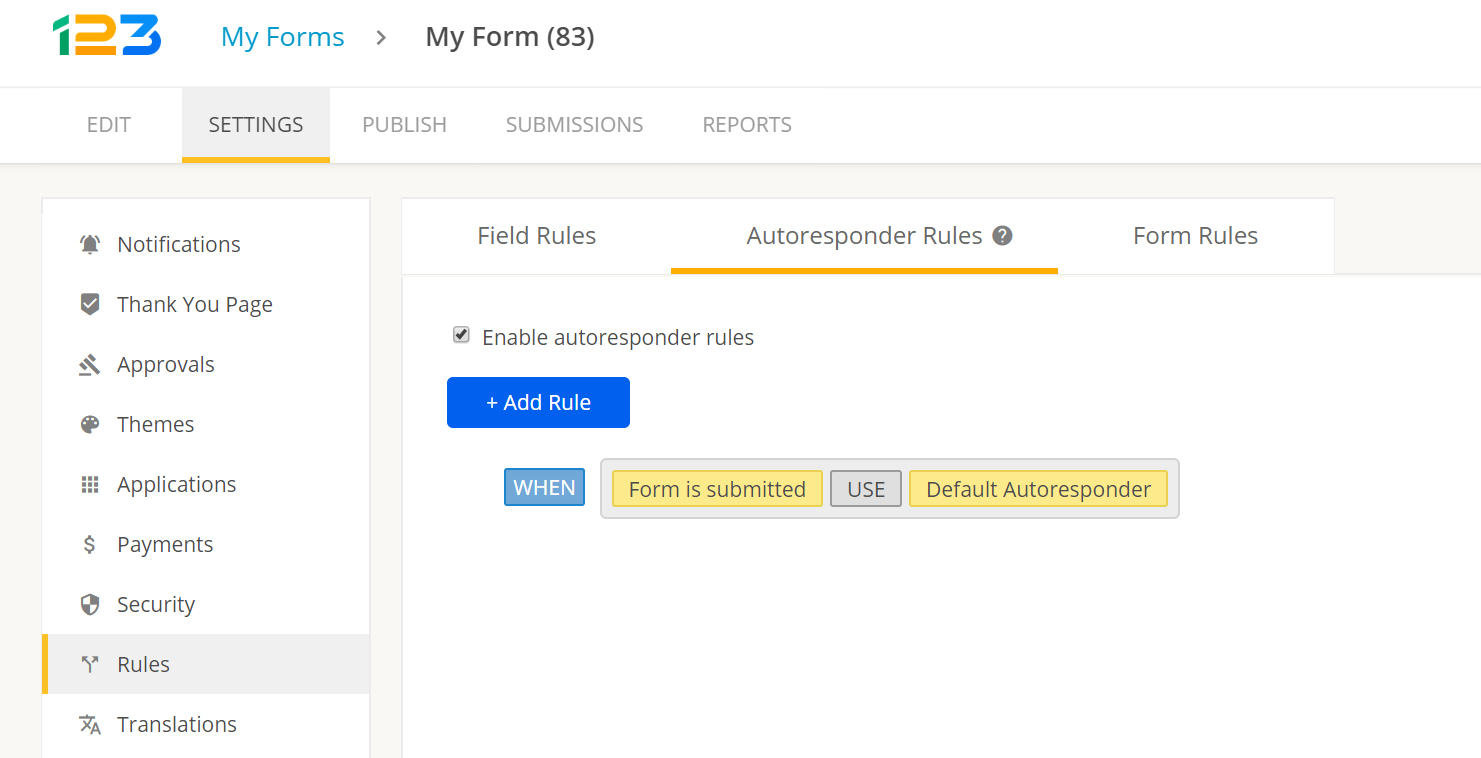
Вот и все; теперь вы можете официально играть с правилами формы до конца света и обратно. Как вы обнаружите, вопросы, варианты выбора и персонализация могут быть благом для вашего сайта, независимо от того, с чем он может иметь дело.Короткие формы, длинные формы — все они могут использовать условное ветвление, чтобы создать уникальный опыт для пользователей (и, таким образом, помочь вам конвертировать больше, поскольку 80% пользователей больше склонны покупать у компаний, которые персонализируют их путешествие).

Рекомендации по формированию условных вопросов и ответов

Может показаться, что это не так, но примеры логических форм есть повсюду.

Нет, правда. Викторина Buzzfeed? Эта форма заказа? Та подписка на информационный бюллетень, на которую вы нажали «Да», потому что они давали 10% скидку на обувь?

Условные логические формы, все они!

Какие передовые методы следует учитывать при формировании условных вопросов, ответов и форм в целом?

Держите:

1. Простота — ключ к успеху. Чем проще ваша структура формы и чем легче ей следовать, тем больше вероятность того, что люди будут ей следовать.
2. Не запрашивайте больше информации, чем вам нужно. Накопление данных ни к чему не приведет; это просто забьет ваши системы и подвергнет вас опасности. Так что забудьте про номер обуви и имя первенца, придерживайтесь азов.
3. Не задавайте вопросов, которые заставляют людей искать информацию. Например, их номер социального страхования или имена всех их одноклассников в средней школе.Когда вы делаете это, вы резко «повышаете» шансы, что люди забудут о вашей форме и продолжат жить своей жизнью (🙁).
4. Дайте понять. Кристально чистый. Вы не хотите, чтобы люди «угадывали» поля, которые они должны заполнить, и те, которые являются необязательными, и вы также хотите избежать появления этих надоедливых сообщений об ошибках. Это все о создании плавного взаимодействия, поэтому сделайте его мягким и пушистым для пользователей — от самого начала до самого конца.
5. Проверьте свою форму. Это должно иметь смысл и соединять все возможные точки, которые вы можете себе представить. Вы же не хотите, чтобы ваша форма условной логики потерпела неудачу из-за логической ошибки, верно?
6. A / B тестируйте и свои формы. Тестирование на функциональность — это одно, но экспериментировать, чтобы увидеть производительность и эффективность вашей формы — совсем другое дело. A / B-тест может помочь вам определить, повлияет ли удаление или добавление дополнительных полей в вашу условную форму на коэффициенты конверсии, количество подписок или, в целом, на то, как люди взаимодействуют с вашей формой (и, вместе с этим, с вашим бизнесом).
7. Подбирайте слова с умом. Это может быть само собой разумеющимся, но выбор слов чрезвычайно важен, потому что он определит тип действий, которые предпримут ваши пользователи.

Условная логика может показаться ошеломляющей игрой, но, тем не менее, это забавная игра. Как только вы научитесь его использовать, вы обнаружите, что создатель формы (подмигивание, подмигивание и т. Д.) Может быть скупой, скудной машиной преобразования.

Так почему ты еще не получил свой?

.

История логики | Британника

Предшественники древней логики

Существовала средневековая традиция, согласно которой греческий философ Парменид (V век до нашей эры) изобрел логику, живя на скале в Египте. Эта история — чистая легенда, но она отражает тот факт, что Парменид был первым философом, который использовал расширенные аргументы в пользу своих взглядов, а не просто предлагал видение реальности. Но использование аргументов — это не то же самое, что их изучение, и Парменид никогда систематически не формулировал и не изучал принципы аргументации как таковые.В самом деле, нет никаких свидетельств того, что он хотя бы знал о неявных правилах вывода, использованных при изложении его доктрины.

Возможно, аргументация Парменида была вдохновлена ​​практикой древнегреческой математики среди пифагорейцев. Таким образом, примечательно, что у Парменида, как сообщается, был учитель-пифагорей. Но история пифагореизма в этот ранний период окутана тайной, и трудно отделить факт от легенды.

Если Парменид не знал общих правил, лежащих в основе его аргументов, то, возможно, это не так для его ученика Зенона Элейского (V век до н. Э.).Зенон был автором многих аргументов, известных под общим названием «Парадоксы Зенона», с целью вывести невозможные последствия из непарменидовского взгляда на вещи и, таким образом, опровергнуть такую ​​точку зрения и косвенно установить монистическую позицию Парменида. Логическая стратегия обоснования претензии путем демонстрации того, что ее противоположность приводит к абсурдным последствиям, известна как reductio ad absurdum. Тот факт, что все аргументы Зенона были в этой форме, предполагает, что он осознавал и размышлял над общей закономерностью.

Парадокс Зенона, иллюстрируемый Ахиллесом в гонке на черепахе. Британская энциклопедия, Inc.
Britannica Premium: удовлетворение растущих потребностей искателей знаний. Получите 30% подписки сегодня.
Подпишись сейчас

Другие авторы тоже способствовали растущему интересу греков к умозаключениям и доказательствам. Ранние риторы и софисты — например, Горгий, Гиппий, Продик и Протагор (все 5 век до нашей эры) — культивировали искусство защиты или критики тезиса с помощью аргументов. Эта забота о методах аргументации иногда просто приводила к вербальному проявлению навыков ведения дискуссии, которые Платон называл «эристикой».Но верно также и то, что софисты сыграли важную роль в доведении аргументации до центральной позиции, которую она заняла в греческой мысли. Например, софисты были среди первых людей, которые потребовали, чтобы моральные претензии были оправданы причинами.

Определенные учения софистов и риторов важны для ранней истории логики. Например, Сообщается, что Протагор был первым, кто различал разные типы предложений: вопросы, ответы, молитвы и предписания.Продик, кажется, утверждал, что никакие два слова не могут означать одно и то же. Соответственно, он уделял много внимания тщательному различению и определению значений очевидных синонимов, включая многие этические термины.

Сократ ( c. 470–399 до н. Э.), Как говорят, посещал лекции Продика. Как и Продик, он следовал определениям вещей, особенно в области этики и ценностей. Эти исследования, проведенные посредством дебатов и аргументов, как это описано в трудах Платона (428 / 427–348 / 347 гг. До н. Э.), Усилили интерес греков к аргументации и подчеркнули важность осторожности и строгости в использовании языка.

Платон продолжил работу, начатую софистами и Сократом. В Sophist он отличил утверждение от отрицания и провел важное различие между глаголами и именами (включая существительные и прилагательные). Он заметил, что полное заявление ( логотипов ) не может состоять из одного только имени или глагола, но требует по крайней мере одного из них. Это наблюдение указывает на то, что анализ языка развился до точки исследования внутренней структуры высказываний в дополнение к отношениям высказываний в целом друг к другу.Это новое развитие было возведено в высокое искусство учеником Платона Аристотелем (384–322 до н. Э.).

Платон беседует со своими учениками Платон беседует со своими учениками, мозаика из Помпеи, I век до н. в Национальном археологическом музее Неаполя. К. М. Диксон / Heritage-Images

В произведениях Платона есть отрывки, в которых он предполагает, что практика аргументации в форме диалога (платоновская «диалектика») имеет большее значение, чем ее периодическое использование для исследования конкретной проблемы.Предполагается, что диалектика — это самостоятельная наука или, возможно, общий метод достижения научных выводов в других областях. Эти основополагающие, но неубедительные замечания указывают на новый уровень общности греческих рассуждений о рассуждениях.

.

определение логики Free Dictionary

Logic

процесс рассуждения от следствия к причине, основанный на наблюдении.

1. метод априорных рассуждений, то есть дедуктивного рассуждения, от причины к следствию или от общего к частному.
2. априорный принцип .

мнемоническое слово, представляющее силлогистический аргумент на первом рисунке, в котором есть две универсальные утвердительные посылки и универсальный утвердительный вывод.

мнемоническое слово, представляющее силлогистический аргумент на четвертом рисунке, в котором есть две универсальные утвердительные посылки и конкретный положительный вывод.

мнемоническое слово для обозначения силлогистического аргумента на втором рисунке, в котором есть одна универсальная утвердительная и одна конкретная отрицательная посылка и конкретный отрицательный вывод.

мнемоническое слово для обозначения силлогистического аргумента на третьем рисунке, в котором есть одна конкретная отрицательная, одна универсальная утвердительная посылка и конкретный отрицательный вывод.

мнемоническое слово, представляющее силлогистический аргумент на втором рисунке, в котором есть одна универсальная утвердительная и одна универсальная отрицательная посылка и универсальный отрицательный вывод.

мнемоническое слово, представляющее силлогистический аргумент на первом рисунке, в котором есть одна универсальная отрицательная, одна универсальная утвердительная посылка и универсальный отрицательный вывод.

мнемоническое слово для обозначения силлогистического аргумента на втором рисунке, в котором есть одна универсальная отрицательная, одна универсальная утвердительная посылка и универсальный отрицательный вывод.

мнемоническое слово, обозначающее силлогистический аргумент на третьем рисунке, в котором есть две универсальные утвердительные посылки и конкретное положительное заключение.

мнемоническое слово для обозначения силлогистического аргумента на первом рисунке, в котором есть одна универсальная утвердительная посылка, одна конкретная утвердительная посылка и конкретный положительный вывод.

мнемоническое слово для обозначения силлогистического аргумента на третьем рисунке, в котором есть одна универсальная утвердительная посылка, одна конкретная утвердительная посылка и конкретный положительный вывод.

1. выражение, которое должно быть определено в терминах ранее определенного выражения.
2. все, что необходимо определить. — Definienda , n., Pl .

Диматис.

мнемоническое слово, представляющее силлогистический аргумент на четвертом рисунке, в котором есть одна универсальная утвердительная посылка, одна утвердительная посылка и конкретный положительный вывод. Также называется Dimaris .

мнемоническое слово, обозначающее силлогистический аргумент на третьем рисунке, в котором есть одна конкретная утвердительная и одна универсальная утвердительная посылка и конкретный положительный вывод.

силлогистический аргумент, который опровергает предложение, доказывая прямо противоположное его заключению. — elenchic, elenctic , adj .

силлогизм, в котором истинность одной из предпосылок подтверждается прилагаемым предложением (прозиллогизм) , что приводит к формированию составного аргумента. См. Также прозиллогизм .

равенство двух или более предложений, например, когда два предложения имеют одинаковое значение, но выражаются по-разному.См. Также соглашение.

мнемоническое слово для обозначения силлогистического аргумента на третьем рисунке, в котором есть одна универсальная отрицательная, одна универсальная утвердительная посылка и конкретный отрицательный вывод.

мнемоническое слово, представляющее силлогистический аргумент на первом рисунке, в котором есть одна универсальная отрицательная и одна конкретная утвердительная посылка и конкретный отрицательный вывод.

мнемоническое слово, представляющее силлогистический аргумент на третьем рисунке, в котором есть одна универсальная отрицательная, одна конкретная утвердительная посылка и конкретный отрицательный вывод.Также Ferison .

Ферисо.

мнемоническое слово для обозначения силлогистического аргумента на четвертом рисунке, в котором есть одна универсальная отрицательная, одна универсальная утвердительная посылка и конкретный отрицательный вывод.

мнемоническое слово для обозначения силлогистического аргумента на втором рисунке, в котором есть одна универсальная отрицательная, одна конкретная утвердительная посылка и конкретный отрицательный вывод.

мнемоническое слово, представляющее силлогистический аргумент на четвертом рисунке, в котором есть одна универсальная отрицательная, одна конкретная утвердительная посылка и конкретный отрицательный вывод.

метафизика или метафизические аспекты логики. — металогический , прил .

множественная дилемма или дилемма с множеством одинаково неприемлемых альтернатив; тяжелое положение.

силлогизм, связанный с другим таким образом, что вывод первого является предпосылкой следующего.

форма или характер силлогизма.

эллиптический ряд силлогизма, в котором посылки устроены так, что сказуемое первого является подлежащим следующего, продолжаясь таким образом до тех пор, пока подлежащее первого не объединится с предикатом последнего.- соритический, соритовый , прил. .

форма рассуждения, в которой формулируются два предложения или посылки и из них делается логический вывод. Каждая посылка имеет форму субъект-предикат, и каждая имеет общий элемент, называемый средним термином .

принципы или практика синтеза или синтетические методы или техники, то есть процесс дедуктивного рассуждения, от причины к следствию, от простых элементов к сложному целому и т. Д.

.