Как решают нестандартные задачи: Книга: «Как решают нестандартные задачи» — Канель-Белов, Ковальджи. Купить книгу, читать рецензии | ISBN 978-5-4439-2621-6
Как решают нестандартные задачи — Канель-Белов А.Я., Ковальджи А.К.
Название: Как решают нестандартные задачи.
Автор: Канель-Белов А.Я., Ковальджи А.К.
2008.
В книге описан ряд классических идей решения олимпиадных задач, которые для большинства школьников являются нестандартными. Каждая идея снабжена комментарием, примерами решения задач и задачами для самостоятельного решения. Приведены подборки задач олимпиадного и исследовательского типов (всего 200 задач), которые сгруппированы по классам.
Сборник адресован старшеклассникам, учителям, руководителям кружков и всем любителям математики.
Предыдущее издание вышло в 2004 г.

Решение олимпиадных задач служит хорошей подготовкой к будущей научной деятельности, заостряет интеллект.
На основе опыта работы в Вечерней математической школе мы отобрали задачи, часто используемые на занятиях математических кружков. Эти задачи, интересные и сами по себе, служат материалом для описания ряда общематематических идей решения задач.
В книге описаны классические идеи1 решения олимпиадных задач. К этим идеям подобраны примеры решения задач и задачи для самостоятельного решения. Сложность задач существенно различна. Для решения некоторых из них достаточно смекалки, логики и пространственного воображения. Другие задачи требуют некоторого опыта, интуиции и наблюдательности. Чтобы решить наиболее трудные задачи потребуется умение организовать работу над задачей (прояснить ситуацию, выявить круг идей, подобрать удобный «язык») и владеть определённой техникой. В части II приведены задачи олимпиадного и исследовательского типов, которые сгруппированы по классам.
Содержание
Предисловие 4
Как работать с книгой 5
Часть I. Идеи и методы решения задач 6
Поиск родственных задач 6
Причёсывание задач (или «можно считать, что…») 8
Доказательство от противного 12
Чётность 13
Обратный ход 15
Подсчёт двумя способами 17
Соответствие 20
Графы 24
Инварианты 29
Метод крайнего 32
Уход на бесконечность и малые шевеления 35
Принцип Дирихле 37
Индукция 40
Делимость и остатки 44
Алгоритм Евклида 46
Покрытия, упаковки и замощения 49
Раскраски 53
Игры 55
Процессы и операции 59
Часть II. Задачи 64
8 класс 65
9 класс 68
10 класс 74
11 класс 78
Приложение 83
Советы участнику олимпиады 83
Критерии оценки работ 84
Математический словарик 85
Обозначения 89
Советуем почитать 90
Купить книгу Как решают нестандартные задачи — Канель-Белов А.Я., Ковальджи А.К. —
Купить книгу Как решают нестандартные задачи — Канель-Белов А.Я., Ковальджи А.К.
По кнопкам выше и ниже «Купить бумажную книгу» и по ссылке «Купить» можно купить эту книгу с доставкой по всей России и похожие книги по самой лучшей цене в бумажном виде на сайтах официальных интернет магазинов Лабиринт, Озон, Буквоед, Читай-город, Литрес, My-shop, Book24, Books.ru.
По кнопке «Купить и скачать электронную книгу» можно купить эту книгу в электронном виде в официальном интернет магазине «ЛитРес», и потом ее скачать на сайте Литреса.
По кнопке «Найти похожие материалы на других сайтах» можно найти похожие материалы на других сайтах.
On the buttons above and below you can buy the book in official online stores Labirint, Ozon and others. Also you can search related and similar materials on other sites.
Дата публикации:
Теги:
решебник по математике :: математика :: Канель-Белов :: Ковальджи :: нестандартные задачи
Смотрите также учебники, книги и учебные материалы:
Следующие учебники и книги:
- Математика (Алгебра. Геометрія). 8 клас. Підсумкові контрольні роботи. Мерзляк А.Г., Полонський В.Б., Прокопенко Н.С., Якір М.С.
- Математика (Алгебра. Геометрія). 7 клас. Підсумкові контрольні роботи. Мерзляк А.Г., Полонський В.Б., Прокопенко Н.С., Якір М.С.
- Математика. 6 клас. Підсумкові контрольні роботи. Мерзляк А.Г., Полонський В.Б., Прокопенко Н.С., Якір М.С.
- Математика. 5 клас. Підсумкові контрольні роботи. Мерзляк А.Г., Полонський В.Б., Прокопенко Н.С., Якір М.С.
Предыдущие статьи:
Как решают нестандартные задачи — Канель-Белов А.Я., Ковальджи А.К.
По кнопке выше «Купить бумажную книгу» можно купить эту книгу с доставкой по всей России и похожие книги по самой лучшей цене в бумажном виде на сайтах официальных интернет магазинов Лабиринт, Озон, Буквоед, Читай-город, Литрес, My-shop, Book24, Books.ru.
По кнопке «Купить и скачать электронную книгу» можно купить эту книгу в электронном виде в официальном интернет магазине «ЛитРес», и потом ее скачать на сайте Литреса.
По кнопке «Найти похожие материалы на других сайтах» можно искать похожие материалы на других сайтах.
On the buttons above you can buy the book in official online stores Labirint, Ozon and others. Also you can search related and similar materials on other sites.
Название: Как решают нестандартные задачи.
Автор: Канель-Белов А.Я., Ковальджи А.К.
2008.
В книге описан ряд классических идей решения олимпиадных задач, которые для большинства школьников являются нестандартными. Каждая идея снабжена комментарием, примерами решения задач и задачами для самостоятельного решения. Приведены подборки задач олимпиадного и исследовательского типов (всего 200 задач), которые сгруппированы по классам.
Сборник адресован старшеклассникам, учителям, руководителям кружков и всем любителям математики.
Предыдущее издание вышло в 2004 г.

Решение олимпиадных задач служит хорошей подготовкой к будущей научной деятельности, заостряет интеллект.
На основе опыта работы в Вечерней математической школе мы отобрали задачи, часто используемые на занятиях математических кружков. Эти задачи, интересные и сами по себе, служат материалом для описания ряда общематематических идей решения задач.
В книге описаны классические идеи1 решения олимпиадных задач. К этим идеям подобраны примеры решения задач и задачи для самостоятельного решения. Сложность задач существенно различна. Для решения некоторых из них достаточно смекалки, логики и пространственного воображения. Другие задачи требуют некоторого опыта, интуиции и наблюдательности. Чтобы решить наиболее трудные задачи потребуется умение организовать работу над задачей (прояснить ситуацию, выявить круг идей, подобрать удобный «язык») и владеть определённой техникой. В части II приведены задачи олимпиадного и исследовательского типов, которые сгруппированы по классам.
Содержание
Предисловие 4
Как работать с книгой 5
Часть I. Идеи и методы решения задач 6
Поиск родственных задач 6
Причёсывание задач (или «можно считать, что…») 8
Доказательство от противного 12
Чётность 13
Обратный ход 15
Подсчёт двумя способами 17
Соответствие 20
Графы 24
Инварианты 29
Метод крайнего 32
Уход на бесконечность и малые шевеления 35
Принцип Дирихле 37
Индукция 40
Делимость и остатки 44
Алгоритм Евклида 46
Покрытия, упаковки и замощения 49
Раскраски 53
Игры 55
Процессы и операции 59
Часть II. Задачи 64
8 класс 65
9 класс 68
10 класс 74
11 класс 78
Приложение 83
Советы участнику олимпиады 83
Критерии оценки работ 84
Математический словарик 85
Обозначения 89
Советуем почитать 90
Купить книгу Как решают нестандартные задачи — Канель-Белов А.Я., Ковальджи А.К. —
Купить книгу Как решают нестандартные задачи — Канель-Белов А.Я., Ковальджи А.К.
Дата публикации:
Теги:
решебник по математике :: математика :: Канель-Белов :: Ковальджи :: нестандартные задачи
Смотрите также учебники, книги и учебные материалы:
Следующие учебники и книги:
- Математика (Алгебра. Геометрія). 8 клас. Підсумкові контрольні роботи. Мерзляк А.Г., Полонський В.Б., Прокопенко Н.С., Якір М.С.
- Математика (Алгебра. Геометрія). 7 клас. Підсумкові контрольні роботи. Мерзляк А.Г., Полонський В.Б., Прокопенко Н.С., Якір М.С.
- Математика. 6 клас. Підсумкові контрольні роботи. Мерзляк А.Г., Полонський В.Б., Прокопенко Н.С., Якір М.С.
- Математика. 5 клас. Підсумкові контрольні роботи. Мерзляк А.Г., Полонський В.Б., Прокопенко Н.С., Якір М.С.
Предыдущие статьи:
Решение нестандартных задач как средство познавательной активности на уроках математики
«Ни один наставник не должен забывать,
что его главнейшая обязанность состоит
в приучении воспитанников к умственному
труду и что эта обязанность более важна,
нежели передача самого предмета»
К.Д.Ушинский
Одна из важных задач современной школы — создание в системе обучения таких условий, которые бы способствовали развитию ребенка, раскрытию его творческого потенциала. Дорог каждый день жизни детей, начиная с самого рождения, а тем более нельзя упустить время в первые школьные годы.
Усвоение знаний – большой и нелегкий труд. Он требует от учащихся максимальной отдачи и интеллектуальных сил, длительных и напряженных усилий, постоянной мобилизации воли и внимания. Учение требует особой мотивации, создание у учащихся побудительных сил и потребностей в приобретении знаний, то есть того, из чего складываются умения и желание учиться в школе, а затем самостоятельно овладевать знаниями. От нас, учителей, требуется определение условий, обеспечивающих высокую познавательную активность учащихся в процессе обучения. Важно не только разработать учебный материал, но и тщательно отобрать средства усвоения, обеспечив способ организации усвоения. От того, насколько сформировано мышление у ребёнка, поступающего в школу, будет во многом зависеть успешность обучения вообще, и математике в частности.
Курс математики, направленный на развитие и совершенствование познавательных способностей имеет свои особенности и одна из таких особенностей – смещение акцента на усиление роли содержательно-логических заданий для развития познавательных способностей, познавательной активности учащихся.
Познавательная активность является социально значимым качеством личности и формируется у школьников в учебной деятельности. Она отражает определенный интерес младших школьников к получению новых знаний, умений и навыков, внутреннюю целеустремленность и постоянную потребность использовать разные способы действия к наполнению знаний, расширению знаний, расширение кругозора.
Существенным педагогическим средством, направленным на развитие внутренней потребности интеллектуального роста и познавательной активности, является использование нестандартных математических задач. Речь идет не о задачах, трудных для решения, а о задачах, нестандартных по своей тематике. А Л.М.Фридман считает, что «Нестандартные задачи — это такие, для которых в курсе математики не имеется общих правил и положений, определяющих точную программу их решения».
Нестандартные задачи находят все более частое и широкое применение в обучении математике. Эти задачи можно встретить не только в учебниках математики, пособиях к ним, основной методической литературе, но и в дидактических и наглядных пособиях (диафильмах, ЦОРах, тетрадях на печатной основе и др.).
Нестандартные задачи необходимо подбирать в соответствии с возрастными особенностями школьников и требованиями программы по начальному образованию Федерального компонента государственного стандарта общего образования. Эффективность обучения младших школьников решению нестандартных задач зависит от нескольких условий.
Во-первых, задачи следует вводить в процесс обучения в определенной системе с постепенным нарастанием сложности, так как непосильная задача мало повлияет на развитие учащихся.
Во-вторых, необходимо предоставлять ученикам максимальную самостоятельность в поиске решения задач, давать возможность пройти до конца по неверному пути, убедиться в ошибке и вернуться к началу и искать другой, верный путь решения.
В-третьих, нужно помочь учащимся осознать некоторые способы, приемы, общие подходы к решению нестандартных арифметических задач.
Взяв установку на развитие у учащихся мыслительных операций, познавательной активности, обучая их приемам решения нестандартных заданий, я придерживаюсь следующей системы работы:
- Работа с числами, числовым рядом (магические квадраты).
- Работа с геометрическим материалом (танграммы).
- Работа с фигурами.
- Работа с задачами.
- Анализ результатов работы.
В своей системе работы выделяю следующие направления:
Работа с числами, числовым рядом (магические квадраты)
Числовой ряд
— После изучения чисел первого десятка я предлагаю детям задания — рассмотри ряд чисел. Что интересного заметил? Попробуй продолжить этот ряд чисел.(для выполнения этого задания дети должны хорошо знать прямой и обратный счет в пределах 10).
41,42,43, …, …, ….
91,81,71, …, …, ….
Нужно учитывать, что не все дети знают двузначные числа и для них это будет открытием. При выполнении этого задания ребята обращают внимание не на число, а на запись и порядок цифр в этом числе. Постепенно задание усложняется.
— Продолжи ряд чисел:
109,208,307,…., …,
В этом ряду в числах изменяются уже две цифры.
Дальше задания еще больше усложняются (для выполнения этого задания дети должны понимать понятия увеличить и уменьшить на несколько единиц и выполнять действия в пределах 10). Формулировка задания остается такая же.
2,4,3,5,4,6,7…… (сначала увеличиваем на два, затем уменьшаем на 1)
9,6,8,5,7,4,……. (сначала уменьшаем на 3, затем увеличиваем на 2) и т. д.
Магические квадраты
На этапе подготовки, прежде всего, детям необходимо объяснить, в чем собственно заключается магия. И первыми задачами могут быть задачи с требованием проверить, является ли квадрат, магическим. Обязательно рассматриваем квадрат.
— Заполни цифрами квадрат так, чтобы сумма чисел по всем направлениям была равна 15.
| 3 |
|
| 5 |
|
2 |
|
|
После подготовки целесообразно обратиться к детям с вопросом: «Вы можете получить магический квадрат?» Предложить им попробовать.
Обычно дети начинают подставлять числа в клеточки квадрата хаотично, затрудняясь при этом обосновывать свои действия. Но даже при таком беспорядочном переборе возможно, что один из вариантов расположений чисел в квадрате учащиеся смогут найти.
Задача учителя состоит в том, чтобы подчеркнуть мысль о целесообразности упорядочного перебора вариантов со случайным подбором. Как его организовать? Можно выполнить следующее.
— Какие существуют суммы по три числа от 1 до 9, равные 15? (1+5+9, 1+6+8, 2+4+9, 2+5+8, 2+6+7, 3+4+8, 3+5+7, 4+5+6, всего восемь сумм.)
— Во сколько разных сумм входит число, стоящее в центре квадрата? (в четыре суммы: две диагонали, один столбец, одна строка)
— Какое число стоит в центре квадрата? (5)
— Во сколько разных сумм входит число, стоящее в углу квадрата? (В три суммы: (одна диагонали, один столбец, одна строка)
— Какие числа от 1 до 9 входят в три суммы из имеющихся восьми? (Это все четные числа)
— Их можно расставить в углах квадрата.
— Далее однозначно заполняются все остальные клетки.
Рассуждая так, дети могут найти несколько разных магических квадратов.
Работа с геометрическим материалом (танграммы)
— Нарисуй такую же фигуру без отрыва карандаша от бумаги и не проводи два раза одну и ту же линию.
— Из каких знакомых тебе фигур состоит эта фигура:
В рамках решения нестандартных заданий, использую задачи на моделирование: задания на составление заданных фигур из определенного числа одинаковых палочек и задания на изменения заданной фигуры.
— Как переложить 1 палочку, чтобы из 2 треугольников получилось 3 треугольника.
— отсчитайте пятнадцать счетных палочек и по данному образцу выложите пять квадратов.
Отыщите квадрат, у которого больше всего общих сторон. Сколько общих сторон? (3)
Даны 3 ряда изображений кошек, составленных из геометрических фигур. Недостающую в третьем ряду нужно найти на основе анализа, сравнения и обобщения.
После выполнения таких заданий, ребята стараются составить свои аналогичные задания.
Работа с фигурами
Нестандартные решения сложных задач / Хабр
Меня интересуют различные методы системного и творческого мышления, которое можно использовать в реальной жизни для решения сложных задач. О нескольких методах расскажу в данной статье.
Недавно прочитал книгу Торп С. — Учебник креативного мышления. Простой подход к нестандартным решениям – 2010. В ней предлагается интересный подход для развития навыков решения сложных задач.
Основная мысль автора – чтобы решать сложные задачи, нужно сворачивать с колеи шаблонного мышления, нарушать правила, которые зачастую нам не дают взглянуть на проблему шире. Вот что пишет автор:
Неспособность разрешить какую-то проблему вполне может объясняться тем, что вы застряли в «колее» правил. Мы все живем по правилам — укоренившимся в нас шаблонам мышления, которые ошибочно принимаем за истину. Наши правила формируются естественным образом в результате многократного использования одних и тех же идей. Следуя правилам, мы постепенно увязаем в глубокой «колее», и тогда любые неординарные идеи остаются вне нашего поля зрения.
Как нарушать правила, отлично показано на примере игры «Крестики-нолики».
Многие неразрешимые проблем похожи на игру в «крестики-нолики»» Выигрыш кажется невозможным, как бы ты не играл. Однако нарушив (или расширив) правила можно получить победу множеством путей.
Ход вне очереди
В «крестики-нолики» выиграть очень просто, если делать ходы вне очереди! Конечно в контексте крестиков-ноликов, нарушение правил – это обман. Однако речь идет не о моральных принципах, а о правилах, которые предписывают нам, как следует решать проблему.
Если правила не работают, то почему бы не сыграть на опережение, делая дополнительные ходы.
Мало кому приходит в голову сделать ход вне очереди в реальном мире, но, в сущности, этот прием используется с незапамятных времен. Например, после одного из сражений гражданской войны в Америке генерал Роберт Ли объявил своим офицерам, что генерал Грант двинется на Спотсильванию, так как это наилучшее для него решение. Ли разработал кратчайший маршрут к этому пункту и приказал войскам двигаться туда. Войска Ли сделали, так сказать, ход вне очереди и прибыли в Спотсильванию прежде, чем туда смогла добраться армия Гранта.
Ходы вне очереди — распространенное явление в мире бизнеса. Когда изготовители Тайленола узнали, что аналогичное обезболивающее средство Датрил будет продаваться со значительной скидкой, они сделали ход вне очереди. Они установили цену ниже стоимости Датрила еще до того, как изготовители последнего смогли объявить о своей цене. Рекламная кампания нового лекарства провалилась, и Тайленол удержал свои позиции на рынке.
Мы в компании, часто играем на опережение – ещё на предварительном изучении объекта автоматизации разрабатываем прототип системы. Такой подход нам позволяет глубже понять, что нужно сделать, а заказчику увидеть серьёзность наших намерений.
Используйте активы соперника
Выстроить в ряд три значка совсем не трудно, если к своим двум ноликам прибавить чужой крестик. Зачем ограничивать себя собственными ресурсами? )
Адмирал военно-морского флота США Гарри Ярнелл был первым, кто разработал план нападения японцев на Перл-Харбор. Он определил наиболее перспективные направления и стратегию атаки. В 1932 году он даже провел показательные учения с участием двух авианосцев США. Императорский военно-морской флот Японии превратил план американского адмирала в собственную успешную атаку на базу ВМС США. Японцы не постеснялись воспользоваться американским планом сражения. Если план эффективен, осознано используйте его, независимо от источника.
В шашках и шахматах победная комбинация основывается на расположении, как своих фигур, так и противника, причем именно использование фигур противник зачастую является ключевым элементом победного плана.
В бизнесе предприниматели часто изучают что сдали конкуренты, учитывают их ошибки и создают более прибыльную систему.
Проявите гибкость (и правильно ставьте задачи)
Вы сможете выиграть в «крестики-нолики» или разрешить другие сложные задачи, если примените гибкое определение термина «победа». Позвольте вашему ряду изогнуться, и победа у вас в кармане. Иногда определенные нами условия победы слишком строги или не соответствуют характеру сложившейся ситуации. Измените определение успеха и решение станет возможным.
Кроме того, если задача была поставлена неправильно, то возможно никому не под силу её решить. Задача должна ставиться конструктивно, в расчете на нетривиальные решения, отличные от ваших первоначальных ожиданий. Деструктивная постановка задач связана с таким количеством условий и ограничений, что достижение цели оказывается за пределами человеческих возможностей. Примером деструктивной постановки задачи может быть желание «летать, махая руками, словно крыльями».
При конструктивной постановке задачи приемлемым будет любое решение, позволяющее вам «оторваться от земли». Правильная постановка задачи расширяет диапазон возможных решений.
Сотрудничайте
Правило, ведущее к обязательному проигрышу одной стороны, может оказаться самым большим препятствием на пути к победе любого из участников игры. Сотрудничество с соперником может обеспечить выигрыш вам обоим.
Однажды я услышал фразу на всегда запавшую мне в душу: «В одного можно вырастить только супер-картошку!!». Имеется ввиду, что для решения действительно сложных задач нужна команда и желание сотрудничать.
Пробуйте решать сложные проблемы – нарушайте правила!
Нестандартное решение задач. (исследовательская работа)
Слайд 1
Нестандартное решение задач Автор Козьмина Татьяна, 14 лет, ученица 8 класса, МКОУ «Тальменская СОШ №3», руководитель Перетокина Валентина Борисовна. Муниципальное казенное общеобразовательное учреждение «Тальменская средняя общеобразовательная школа №3»
Слайд 2
Введение Решение олимпиадных задач заостряет интеллект. Для того, чтобы научиться решать задачи конкурсного типа самостоятельно, необходимо ознакомиться с некоторым минимумом решения таких задач этот минимум не должен состоять из большого числа задач.
Слайд 3
Актуальность Нестандартные задачи способствуют повышению мотивации к изучению математики; развивают мышление и творческую активность; формируют умения и навыки для решения практических задач.
Слайд 4
Цель: изучить методы решения некоторых, наиболее часто встречающихся, видов школьных математических нестандартных задач Задачи: Изучить различные методы решения нестандартных задач; п рименить рассматриваемые приемы, методы и подходы при решении конкретных задач; развивать интерес к математике.
Слайд 5
Гипотеза: Имеется ли единый подход к решению нестандартных задач или он отсутствует.
Слайд 6
Объект исследования : некоторые виды нестандартных задач по математике. Предмет исследования: решение задачи — как объект конструирования и изобретения.
Слайд 7
Виды нестандартных задач: Алгоритм Евклида; инварианты; задачи на раскраску; логические задачи; арифметические задачи; задачи на разрезание; задачи на переливания; задачи на движение; задачи на взвешивания; задачи на выигрышные ситуации; геометрические задачи.
Слайд 8
Инварианты Задача 2. В каждой клетке доски 7х7 сидит гусеница. В некоторый момент все гусеницы переползают на соседние (по стороне) клетки. Обязательно ли после этого останутся пустые клетки? Решение: Так как общее число клеток шахматной доски 7×7 клеток нечетно, то черных и белых клеток не может быть поровну. Пусть для определенности черных клеток больше. Тогда гусениц, сидящих на белых клетках, меньше, чем черных клеток. Поэтому хотя бы одна из черных клеток останется пустой, так как на черные клетки переползают только жуки. сидящие на белых клетках.
Слайд 9
Задача на разрезание Задача 1. При помощи ножниц вырежьте в тетрадном листе дырку, через которую мог бы пролезть слон. Решение:
Слайд 10
Задачи на переливания Задача 3. Как при помощи 5-ти литрового и 9-ти литрового ведра набрать из реки 3 литра воды? Решение: Заполняем водой из реки 9-ти литровое и переливаем из него воду в 5-ти литровое (в 9-ти литровом остается 4 литра). Освобождаем 5-ти литровое ведро и переливаем в него 4 литра из 9-ти литрового. Еще раз заполняем водой из реки 9-ти литровое и из него доливаем в 5-ти литровое 1 литр воды (в 9-ти литровом остается 8 литров). Освобождаем 5-ти литровое и переливаем в него из 9-ти литрового 5 литра воды. В 9-ти литровом ведре останется 3 литра воды.
Слайд 11
Задачи на движения Задача 4. Два теплохода одновременно вышли из портов и с постоянной скоростью движутся во встречном направлении. Скорость одного теплохода 20 км/час, другого – 30 км/час. На каком расстоянии друг от друга они будут находиться ровно за один час до их встречи? Решение: 1) 20+30=50 (км.) – расстояние друг от друга за 1 час до их встречи. Ответ: 50 километров.
Слайд 12
Логические задачи Задача 5. Три курицы за три дня несут три яйца. Сколько яиц снесут 12 таких же курей за 12 дней? Решение: 1 курица – 1 яйцо за 3 дня. 1 курица – 4 яйца за 12 дней, значит, 12 курей за 12 дней – 12х4 = 48 яиц. Ответ: 4 8 яиц.
Слайд 13
Вывод Каждая задача уникальна, общих правил для решения нестандартных задач нет . Процесс решения нестандартной задачи: 1) Сведение (путем преобразования или переформулирования) нестандартной задачи к другой, ей эквивалентной, но уже стандартной задаче; 2) Разбиение нестандартной задачи на несколько стандартных подзадач. Гипотеза подтвердилась: рассмотрение решения нескольких нестандартных текстовых задач позволило сделать вывод об отсутствии единого подхода к решению нестандартных математических задач, несмотря на наличие общих рекомендаций для решения того или иного вида школьных текстовых задач.
Слайд 14
Заключение Применение нестандартных методов решения задач по математике, довольно часто помогает быстрее и легче решить сложные задания, но что бы решать таким образом требуется нетрадиционное мышление, умение мыслить не по шаблону.
Слайд 15
Использованная литература: А. Я. Канель-Белов , А. К. Ковальджи «Как решаются нестандартные задачи» — Под ред. В. О. Бугаенко . 4-е изд., МЦНМО, 2008. Интернет-ссылки: http://900igr.net/prezentacija/algebra/issledovatelskij-proekt-reshenie-nekotorykh-nestandartnykh-zadach-po-algebre-260629/tsel-raboty-izuchit-metody-reshenija-nekotorykh-naibolee-chasto-3.html http://festival.1september.ru/articles/623951/ http://pptcloud.ru/pedagogika/kak-reshit-nestandartnuyu-zadachu http://900igr.net/prezentacija/pedagogika/nestandartnye-metody-reshenija-zadach-236429.html http://900igr.net/prezentacija/pedagogika/nestandartnye-metody-reshenija-zadach-236429/vstuplenie-2.html https://prezentacii.org/prezentacii/prezentacii-po-matematike/6412-reshenie-nestandartnyh-zadach.html http://www.myshared.ru/slide/803596/
Слайд 16
Спасибо за внимание!
| |||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||
| 2011 — 2018 | |||||||||||||||||||||||||||||||||||||||||||||||
Статья на тему «Нестандартные задачи»
Предисловие
В первые годы своей педагогической деятельности стоял вопрос: как доступно объяснить учащимся ту или иную тему? А вопрос возник из-за того, что школьные учебники сложны для учащихся. (Учителем математики работаю с1980 года.) Многие из них изложены научным, сложным языком, вследствие чего они не являются привлекательным для учащихся. Поэтому я сочла для себя в первую очередь привести всю школьную математическую теорию в систему через алгоритмизацию школьного курса математики. На это ещё подтолкнуло изучение передовых методик на то время. Для меня интересна была методика преподавания математики Р.Г.Хазанкина. По его методике большое место занимает решение ключевых задач. Эти ключевые задачи ученик должен запомнить. А их, сколько в школьном курсе математики? Очень много. В школьных учебниках задачи распределены по группам в соответствии с используемым для их решения математическим аппаратом. Такие задачи учащиеся, как правило, решают неплохо, потому что указана, какая теория должна использоваться. Если же учащиеся лишены такого ориентира, то испытывают затруднения даже при решении несложных задач. Отсюда вывод: надо привести школьную математику в стройную систему. А система такова: школьный курс алгебры состоит из 4 крупных блоков:
1.Числа.
2.Функции.
3.Уравнения и неравенства.
4.Тождества.
В каждом блоке всё взаимосвязано, алгоритмизировано и свои ключевые задачи, которые учащимися запоминаются легко. Например, блок «Функции»: схема изучения такова:
1. Определение функции.
2. График функции.
3. Свойства функции.
Эта схема хороша тем, что учащиеся в 7 классе, приступив к изучению функций, при изучении линейной функции уже запоминают схему изучения всего блока. К каждому пункту схемы разработан алгоритм изучения. Изучение всех элементарных и трансцендентных функций в школьном курсе математики происходит по этой схеме и алгоритму. В итоге на уроках экономится время, которое можно использовать для решения более трудных задач. А сколько сложных задач на применении свойств функции. Особенно это стало актуально после введения ЕГЭ.
А числа? Изучение теории чисел заканчивается в 8 классе. А сколько нестандартных задач в КИМ ЕГЭ? Алгоритмизация школьного курса математики, таким образом, высвобождает некоторое количество часов, отведённых на изучение той или иной темы. А освобождённые часы можно использовать на решение нестандартных задач на уроках же. Причём задачи решаются не только с отдельными, хорошо успевающими учениками, а со всем классом. Систематическое использование нестандартных задач способствует целенапрвленному развитию творческих способностей учащихся, их математическому развитию, формированию у них познавательного интереса и самостоятельности. Такие задачи требуют от школьников наблюдательности, творчества и оригинальности. А развитие эвристического мышления у учащихся всегда было актуально.
Что значит владение математикой? Это есть умение решать задачи, причём не только стандартные, но и требующие известной независимости мышления, здравого смысла, оригинальности и изобретательности. Следует хорошо осознавать тот факт, что любая математическая задача, решаемая на уроках, на внеклассных занятиях или дома, должна обязательно научить учащихся. Решение каждой задачи должно быть шагом вперёд в развитии математических знаний, умений навыков учащихся, должно обогащать их знания опыт, учить ориентироваться в различных задачных ситуациях.
Воспитание творческой активности учащихся в процессе изучения ими математики является одной из актуальных задач, стоящих перед учителем математики в современной школе. Основным средством такого воспитания и развития математических способностей учащихся является задачи. Умением решать задачи характеризуется в первую очередь состояние математической подготовленности учащихся, глубина усвоения учебного материала.
Поэтому вполне оправдано то повышенное внимание, которое уделяется решению задач при обучении математике. Функции задач очень разнообразны: обучающие развивающие, воспитывающие, контролирующие. Решение задач является важнейшим средством формирования у школьников системы основных математических знаний, умений, навыков, ведущей формой учебной деятельности учащихся в процессе изучения математики, одним из основных средств их математического развития. От эффективности использования задач в обучении математике в значительной мере зависит не только качество обучения, воспитания и развития учащихся, но и степень их практической подготовленности к последующей деятельности в любой сфере.
В практике обучения математике воспитывающие функции задач редко выступают в качестве ведущих (в отличие от функций, обучающих и контролирующих). Однако тот или иной элемент воспитания может и должен быть осуществлён через каждую задачу. Либо в процессе её решения, либо в процессе изучения результатов решения. В процессе решения задач имеется возможность наиболее ярко продемонстрировать учащимся политехнический характер математики, её прикладную направленность. Иллюстрируя применение математики к решению практических задач, можно показать, что математика, отражая явления реальной действительности, является мощным средством её познания.
Ориентируя школьников на поиски красивых, изящных решений математических задач, учитель тем самым способствует эстетичскому воспитанию учащихся и повышению их математической культуры. И всё же главная цель задач – развить творческое и математическое мышление учащихся, заинтересовать их математикой, привести к «открытию» математических фактов. Достичь этой цели с помощью одних стандартных задач невозможно.
Осуществляя целенаправленное обучение школьников решению задач с
помощью специально подобранных задач, следует учить наблюдать,
пользоваться аналогией, индукцией, сравнениями и делать соответствующие выводы. Необходимо прививать учащимся навыки не только логического рассуждения, но и прочные навыки эвристического мышления. Иногда для развития навыков эвристического мышления целесообразно несколько изменить условия задач. Так вместо задачи «Докажите, что сумма квадратов пяти последовательных натуральных чисел не может быть квадратом натурального числа » предложить учащимся следующее: «Может ли сумма квадратов пяти последовательных натуральных чисел быть квадратом натурального числа?» В этом случае учащиеся индуктивным путём должны сами сформулировать соответствующую гипотезу и только после этого её доказывать.
Отметим так же, что эффективное развитие математических способностей у учащихся невозможно без использования в учебном процессе задач на сообразительность, задач — шуток, математических ребусов, софизмов.
О литературе, рассматривающей нестандартные задачи.
Количество литературы, где рассматривается тема «Нестандартные задачи» очень большое. В первую очередь – это школьные учебники. В них во все времена в конце учебника был раздел, содержаший задачи повышенной трудности. Их решение требует от учащихся знаний, умений, навыков по какому- нибудь вопросу программного материала. Но мне хочется остановиться на комплекте учебников «Алгебра 7, 8, 9. Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, И.Е. Феоктистов» Эти учебники образуют линию учебных изданий для углубленного изучения алгебры. Учебники включают в себя широкий круг дополнительных вопросов, способствующих прочно отрабатывать приёмы решения различных нестандартных задач. Специфической особенностью учебников данной линии является введение избыточного количества задач и задач из далёкого прошлого, что даёт возможность учителю чаще обращать внимание учащихся на общекультурное значение математики. Эти учебники содержат самые разнообразные по степени сложности задачи. Зная возможности учащихся, учитель может какие-то задачи пропустить, а какие-то предложить только тем ученикам, которые идут опережением в классной работе. Тем самым реализуется учителем личностно ориентированный подход в обучении. Также можно вернуться со всем классом к этим задачам позже, во время итогового повторения. Много задач в этих учебниках на статистику, комбинаторику и теорию вероятностей, а новые стандарты математического образования требуют серьёзного подхода к этим разделам математики.
Для работы с учениками 7-9 классов по решению нестандартных задач имеет серьёзный вес сборник задач по алгебре для 7-9 классов. (Галицкий М. Л., Гольдман А. М., Звавич Л.И.)
Нельзя не упомянуть бессменное учебное пособие для многих поколений любителей математики «Сборник задач по математике для поступающих во втузы. Под редакцией М.И. Сканави.» В этом сборнике задачи части 1 разделены на 3 группы (А, Б, В.) по их нарастающей сложности. Такое деление имеет более или менее условный характер. Однако авторы полагают, что умение решать задачи из группы А должно определять минимально необходимый уровень подготовки учащихся к вступительным экзаменам во втузы. Успешное решение задач из группы Б более высокое качество усвоения школьной программы. К группе В отнесены задачи повышенной трудности. Это нестандартные задачи, практика решения которых полезна для развития и укрепления способности к самостоятельному логическому мышлению, для обогащения своей математической культуры. К части 2 «сборника» отнесены не разделённые на группы по степени трудности дополнительные задачи по алгебре и геометрии, задачи по началам математического анализа, а также задачи на применение координат и векторов. В этом сборнике есть слово к тем, кто готовится к вступительным зкзаменам (нынче надо подразумевать – к ЕГЭ). «Приступая к решению задач из намеченной главы, сначала попробуйте самостоятельно решить те задачи из этой главы, решение которых приведено в «Сборнике». В случае затруднения постарайтесь разобраться в изложенных решениях: уяснить теоретическую основу применённых методов и логику рассуждений.
Не торопитесь решать задачи тем способом, который придёт к Вам в голову. Подумайте, не обнаружится ли лучший, например, менее трудоёмкий, подход к решению? При этом в ходе самого решения допустимо привлечение любых формул, теорем, правил алгебры векторов и преобразований к решению геометрических задач, лишь бы полученный Вами ответ был, в конечном счёте, строго обоснован. Иными словами, Вам разрешается в условиях экзамена переходить границы между разными разделами математики во всех направлениях». Фактически здесь расписана методика решения нестандартных задач.
С 2001 года с введением ЕГЭ федеральный центр тестирования Министерства образования и науки Российской Федерации каждый год выпускает сборники под названием «ЕДИНЫЙ ГОСУДАРСТВЕННЫЙ ЭЗАМЕН математика ». Чтобы их отличить от множества книг под таким же названием цикл этих сборников печатаются в жёлтых обложках. В них 10 или 12 разных вариантов, здесь мало простых задач, здесь есть над чем подумать и самому учителю. Решение каждой задачи в этих книгах – это победа. Здесь нет задач где ученики сразу получат ответ, им приходится не только сильно задуматься над задачей С5, но и подумать и в задаче А1.
Те же слова можно сказать о сборниках под редакцией Ф.Ф. Лысенко «Математика ЕГЭ вступительные экзамены»
Очень много литературы по нестандартным задачам, где родственные по идее решения, сгруппированы вместе. Для первых задач каждой группы даётся более подробное решение, чем для последующих. Второстепенные моменты рассуждений и вычислений, как правило, опускаются. Чтобы не стеснить самодеятельности учащегося. Напротив, принципиальным вопросам, существенным для решения задач, уделяется много места. это Например, это относится к вопросам об утрате корней уравнения и появления посторонних корней, об арифметических корнях, о способах изображения пространственных фигур. Однажды сделанное разъяснение, как правило, не повторяется в последующих задачах. Однако всюду, где это требуется, дана ссылка на номер задачи, в которой помещено соответствующее разъяснение. В этом большая ценность в том, что ученик учится работать дополнительной литературой.
Конечно, нужно обратить внимание на сборники олимпиадных задач разных уровней, в том числе и на наши республиканские «Турнир юных математиков», олимпиада «Юные дарования». Здесь задачи расположены без какой-то видимой системы. Однако, именно в этом «беспорядке» заложена определённая система обучения решению задач. Разнообразные задачи не исключают необходимости их систематизации.
Как в спорте, тренировка юного математика требует затраты многого времени. По этому поводу замечательный советский математик Борис Николаевич Делоне сказал: «Большое научное открытие отличается от хорошей олимпиадной задачи тем, что для решения олимпиадной задачи требуется 5 часов, а получение крупного научного результата требует затраты 5000 часов». Здесь не надо понимать «5000 часов» слишком буквально. Но типичным для математика, который атакует трудную проблему, является способность напряжённого размышления целыми днями. Если задача упорно не выходит, то разумно взяться за другую. Но хорошо вернуться к первоначальной после некоторого перерыва.
ОМЕТОДИКЕ ОБУЧЕНИЯ УЧАЩИХСЯ
РЕШЕНИЮ НЕСТАНДАРТНЫХ
ЗАДАЧ
Какая же задача называется нестандартной? «Нестандартные задачи – это такие, для которых в курсе математики не имеется общих правил и положений, определяющих общую программу их решения» (Фридман Л.М., Турецкий Е.Н. Как научиться решать задачи.) Однако следует заметить, что понятие «нестандартная задача» является относительным. Одна и та же задача может быть стандартной или нестандартной в зависимости от того, знаком решающий задачу со способами решения задач такого типа или нет. Например, задача «Представьте выражение 2х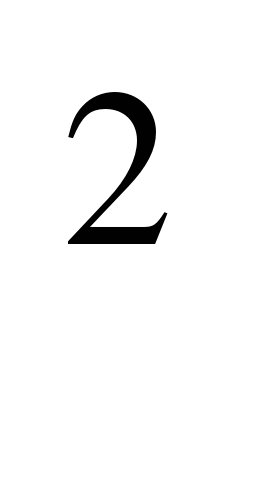 + 2у
+ 2у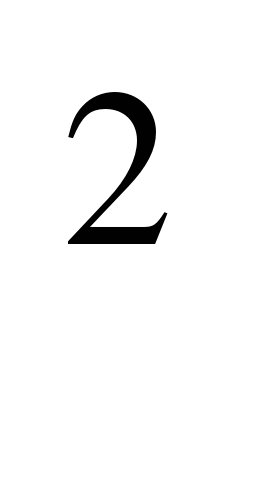 в виде суммы двух квадратов» является для учащихся нестандартной до тех пор, пока учащиеся не познакомились со способами решения таких задач. Но если после решения этой задачи учащимся предложить несколько аналогичных задач, такие задачи становятся для учащихся стандартными.
в виде суммы двух квадратов» является для учащихся нестандартной до тех пор, пока учащиеся не познакомились со способами решения таких задач. Но если после решения этой задачи учащимся предложить несколько аналогичных задач, такие задачи становятся для учащихся стандартными.
Таким образом, нестандартная задача– это задача, алгоритм решения которой учащимся неизвестен, т. е. учащиеся не знают заранее ни способа её решения, ни того, на какой учебный материл учебный опирается решение. Нельзя не согласиться с высказыванием известного математика и методиста Д. Пойа, что, если учитель математики «заполнит отведённое ему ученое время натаскиванием учащихся в шаблонных упражнениях, он убьёт их интерес, затормозит их умственное развитие и упустит свои возможности» (П о й а Д. Как решать задачу.)
Как же помочь учащимся научиться решать нестандартные задачи?
Универсального метода, позволяющего решить любую нестандартную задачу, к сожалению нет, так как нестандартные задачи в какой-то степени неповторимы. Однако опыт многих передовых учителей, добивающихся хороших результатов в математическом развитии учащихся как у нас в стране, так и за рубежом, позволяет сформулировать некоторые методические приёмы обучения учащихся способам решения нестандартных задач.
Прежде всего нужно отметить, что научить решать задачи можно научить только в том случае, если у учащихся будет желание решать задачи, т. е. если задачи будут содержательными и интересными с точки зрения учащихся. Поэтому проблема первостепенной важности, стоящая перед учителем,– вызвать у учащихся интерес к решению той или иной задачи. Необходимо тщательно отбирать интересные задачи и делать их привлекательными для учащихся. Учитель должен уметь находить интересные задачи для учащихся и своевременно предложить ученикам. Наибольший интерес у учащихся вызывают те задачи, взятые из окружающей среды, задачи естественным образом связанные со знакомым учащимся вещами, служащие понятной ученику цели. Например, задача «В комнате стоят стулья и табуретки. У каждой табуретки три ножки, у каждого стула четыре ножки. Когда на всех стульях и табуретках сидят люди, в комнате 39 «ног». Сколько стульев и табуреток в комнате?» Эта задача ещё вызывает у учащихся стимул для приобретения умений и навыков решения неопределённых уравнений первой степени с двумя неизвестными в натуральных и целых числах у учащихся 5- 6 классов.
Конечно, нельзя приучать учащихся решать только те задачи, которые вызывает у них интерес. Но нельзя и забывать, что такие задачи ученик решает легче и свой интерес к решению одной или нескольких задач он может в дальнейшем перенести и на «скучные» разделы.
Таким образом, учитель, желающий научить школьников решать нестандартные задачи, должен вызвать у них интерес к задаче, убедит, что от решения задачи можно получить такое же удовольствие, как от разгадывания кроссвордов.
Далее, задачи не должны быть не слишком лёгкими, но и не должны быть слишком трудными, так как учащиеся, не решив задачу или не разобравшись в решении, предложенном учителем, могут потерять веру в свои силы. Поэтому не следует предлагать учащимся задачу, если нет уверенности, что они смогут её решить.
Ну а как же помочь учащемуся научиться решать задачи, если интерес к решению задач у него есть, и трудности решения его не пугают? В чём должна заключаться помощь учителя ученику, не сумевшему решить интересную для него задачу? Как эффективным образом направить усилия ученика, затруднявшегося самостоятельно начать или продолжить решение задачи?
Прежде всего, не следует идти по самому лёгкому в этом случае пути – познакомить ученика с готовым решением. Не следует и подсказывать, к какому разделу школьного курса математики относится предложенная задача, какие известные учащимся свойства и теоремы нужно применить при решении.
Решение нестандартной задачи – очень сложный процесс, для успешного осуществления которого учащийся должен уметь думать, догадываться. Необходимо также хорошее знание фактического материала, владение общими подходами к решению задач, опыт в решении нестандартных задач.
В процессе решения каждой задачи и ученику, и учителю, обучающему решение задач, целесообразно чётко различать четыре ступени:
1. Изучение условия задачи;
2. Поиск плана решения и его составление;
3 Осуществление плана, т. е. оформление найденного решения;
4. Изучение найденного решения – критический анализ результата решения и отбор полезной информации.
Наблюдения показывают, что даже при решении несложной задачи учащиеся очень много времени тратят на рассуждение о том, за что взяться, с чего начать. Чтобы помочь учащимся найти путь к решению задач, Учитель должен поставить себя на место решающего задачу, попытаться увидеть и понять источник его возможных затруднений. Направить его усилия в наиболее естественное русло. Умелая помощь ученику, оставляющая ему разумную долю самостоятельной работы, позволит учащемуся развить математические способности, накопить опыт, который в дальнейшем поможет находить путь к решению новых задач.
В чём должна заключаться помощь учителя, чтобы обеспечить максимальную самостоятельность учащегося при решении им задачи?
Лучшее, что может сделать учитель для учащегося, состоит в том, что путём неназойливой помощи подсказать ему блестящую идею. Хорошие идеи имеют своим источником прошлый опыт и заранее приобретённые знания. Часто уместным является начать работу с вопроса: «Известна ли вам какая-нибудь родственная задача?» Таким образом, хорошим средством обучения решению задач, средством для нахождения плана решения являются вспомогательные задачи. Умение подбирать вспомогательные задачи свидетельствует о том, что ученик уже владеет определённым запасом различных приёмов решения задач. Если этот запас невелик, то учитель, видя затруднения ученика, должен сам предложить вспомогательные задачи. Умело поставленные наводящие вопросы, вспомогательная задача или система вспомогательных задач помогут понять идею решения. Необходимо стремиться к тому, чтобы ученик испытал радость от решения для него трудной задачи, полученного с помощью вспомогательных задач, наводящих вопросов, предложенных учителем.
Так, если учащиеся затрудняются в решении задачи «Найдите все решения уравнения х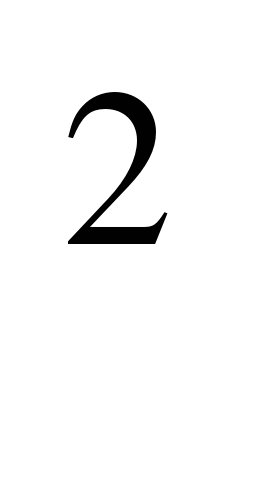 +5у²+4ху+2у+1=0», то можно предложить следующие вспомогательные задачи:
+5у²+4ху+2у+1=0», то можно предложить следующие вспомогательные задачи:
Решить уравнения:
а) (х+1)²+у²=0 (х=-1, у=0)
б) х²-10х+25+у²=0 (х=5, у=0)
в) х²-4х+у²+2у+5=0 (х=2, у=-1)
Учитель, подсказав какой формулой надо воспользоваться для решения задачи, на долю ученика оставляет очень мало. И всё же подсказка гораздо полезнее для ученика. Чем ознакомление с готовым решением: она может создать иллюзию того, что он сам решил предложенную учителем задачу; это даст возможность поверить в свои силы, укрепит его желание решать задачи.
Умение находить вспомогательные задачи, как и вообще умение решить задачи, приобретается практикой. Предлагая ученикам задачу, следует посоветовать выяснить, нельзя ли найти связь между данной задачей и какой-нибудь задачей с известным решением, решающейся проще.
Для приобретения навыков решения довольно сложных задач следует приучать школьников больше внимания уделять изучения полученного решения. Для этого полезно предлагать учащимся видоизменять условие задачи, чтобы закрепить способ её решения, придумывать задачи, аналогичные решённым, более или менее трудные, с использованием найденного при решении основной задачи способа решения.
Проиллюстрируем сказанное примерами. Решив задачу «Докажите, что значение выражения 11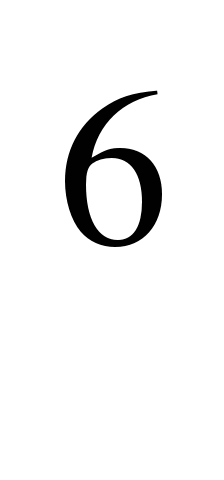 +14
+14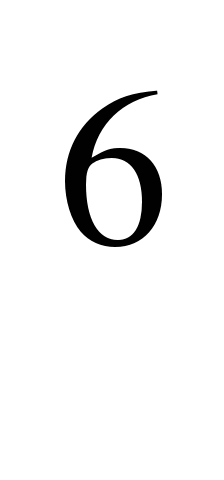 -13
-13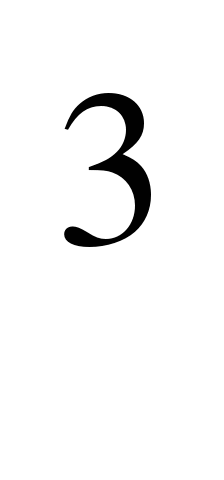 кратно 10», можно для закрепления способа решения предложить учащимся следующие задачи:
кратно 10», можно для закрепления способа решения предложить учащимся следующие задачи:
1. В выражении а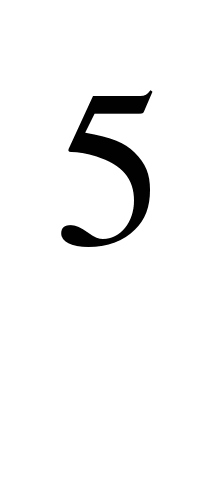 +в
+в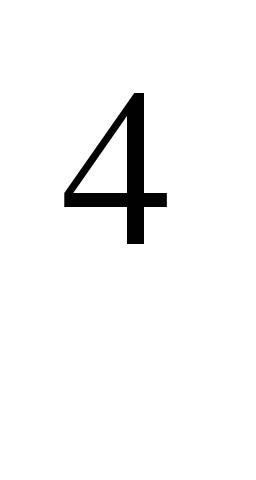 — с
— с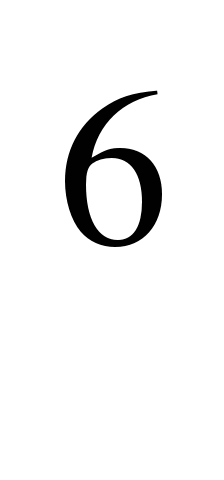 вместо а, в, с подберите трёхзначные числа, чтобы значение полученного выражения было: а) кратно 2; б) кратно 5; в) кратно10. Можно ли, основываясь на применяемом способе решения, подобрать а, в, с так, чтобы получилось выражение кратное 3? Почему?
вместо а, в, с подберите трёхзначные числа, чтобы значение полученного выражения было: а) кратно 2; б) кратно 5; в) кратно10. Можно ли, основываясь на применяемом способе решения, подобрать а, в, с так, чтобы получилось выражение кратное 3? Почему?
2. В выражении 215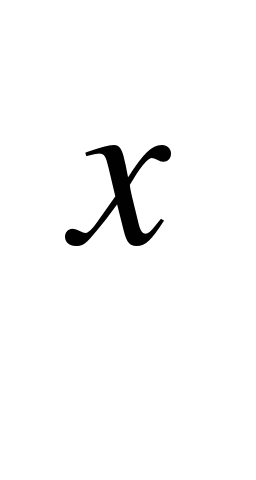 +342
+342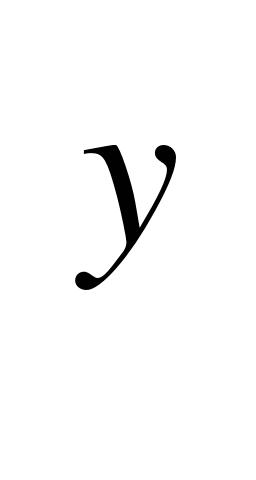 -113
-113 подберите х, у, z такие. Чтобы значение полученного выражения было: а) кратно 2; б) кратно 5; в) кратно10.
подберите х, у, z такие. Чтобы значение полученного выражения было: а) кратно 2; б) кратно 5; в) кратно10.
Решив задачу «В двух бочках воды было поровну. Количество воды в первой бочке сначала уменьшилось на 10%, а затем увеличилось на10%. Количество воды во второй бочке сначала увеличилось на10%, а затем уменьшилось на 10%. В какой бочке воды стало больше?», целесообразно задать детям вопросы: как изменится ответ задачи, если вместо 10% взять 20%, 30%, а%? Какой вывод можно сделать?
Решив задачу: «Имеется лист бумаги. Его разрезают на 4 части, затем некоторые (или все) полученные куски снова разрезают на 4 части и. т. д. Докажите, что при этом Нельзя получить 50 частей листа», полезно изменить её условие так: «Лист бумаги разрезали на 5 частей, на 7 часте й, …, на n частей. Можно ли при этом получить 50 частей? листа? 100 частей листа?…k частей?»
Систематическая работа по изучения способов решения задач поможет учащимся не только решать задачи, но и самим составлять их составлять, анализировать решения. Конструирование задач- интересное занятие, один из верных способов научиться решать задачи.
Умение учащихся составлять нестандартные задачи, решаемые нестандартными способами, свидетельствует о культуре их мышления, хорошо развитых математических способностях.
При анализе решения задачи полезно сопоставить решение данной задачи с раннее решёнными, установить возможность её обобщения.
Учитель постоянно должен помнить, что решение задач не является не самоцелью, а средством обучения. Обсуждение найденного решения, поиск других решений, закрепление в памяти тех приёмов, которые были использованы, выявление условий возможности применения этих приёмов, обобщение данной задачи – всё это даёт возможность школьникам учиться на задаче. При решении задач следует уделить должное внимание оформлению записи найденного решения . Запись решения должна быть четкой и достаточно полной, чтобы, заглянув в нее, можно было восстановить то, что может ученику пригодится при дальнейшем обучении математике
В заключении отметим, что решение задачи крайне сложный процесс, при описании которого невозможно все многообразие его сторон. Дать учащимся правила, позволяющую решить любую нестандартную задачу, невозможно, ибо нестандартные задачи в какой-то степени неповторимы, а универсального метода, позволяющую решить любую задачу, к сожалению нет. Даже строгое выполнение всех указаний и следование советам учителя не сможет творческий процесс отыскания решений нестандартных задач определенные схемы.
Вся совокупность изложенных здесь рекомендаций имеет целью облегчить поиски того пути, который приведет к решению задачи, уменьшив число бесплодных блужданий, неизбежных для каждого учащегося, опыт которого в решении задач невелик.
НАХОЖДЕНИЕ СПОСОБОВ РЕШЕНИЯ НЕСТАНДАРТНЫХ ЗАДАЧ
Общеизвестна роль, которая отводится индукции и наблюдениям при обучении математике учащихся младших классов. Позднее индуктивный метод уступает место дедуктивному. При этом чисто индуктивный поиск способа решения задачи не проводится, решение выполняется дедуктивным способом. В результате от учащихся ускользают пути поиска решения задачи что отрицательно сказывается на их математическом развитии.
Изучение опыта работы учителей убеждает, что при обучении учащихся математике (в частности при обучении учащихся способам решения нестандартных задач) наблюдение и индукция (в том числе и полная) не заняли его должного места. А между тем учитель должен знать и по возможности довести до сознания учащихся тот факт, что математика является экспериментальной, индуктивной наукой. Что наблюдения и индукция играли и играют большую роль при открытии многих математических фактов. Еще Л. Эйлер писал, что свойства чисел, известные сегодня, по большей части были открыты путем наблюдения и открыты задолго до того, как их истинность была подтверждена строгими доказательствами.
Поэтому уже в младших классах школы при обучении математике (да и другим предметам) надо учить школьников наблюдениям, прививать им навыки исследовательской работы, которые могут пригодится в дальнейшем, какой бы вид деятельности они не избрали после окончания школы.
Подчеркивая роль дедуктивных доказательств (доказательств в общем виде), учитель должен обратить внимание учащихся на роль наблюдений и неполной индукции при «открытии» математических закономерностей, при нахождении способа решений самых разнообразных математических задач, на роль полной индукции при обосновании найденных индуктивным путем закономерностей.
Поясним сказанное примерами. Рассмотрим задачу:
«Может ли: а) сумма пяти последовательных натуральных чисел быть простым числом; б) сумма квадратов пяти последовательных натуральных чисел быть простым числом?».
Прежде чем решить эту задачу в общем виде, целесообразно на нескольких частных примерах выяснить , каким числом (простым или составным) могут быть указанные в задаче суммы. С помощью примеров можно получить гипотезы: а) сумма пяти последовательных натуральных чисел — число составное; б) сумма квадратов пяти последовательных натуральных чисел — число составное.
Полученные на примерах (с помощью неполной индукции) гипотезы легко доказываются в общем виде.
Другая задача: «Может ли разность двух трехзначных чисел, из которых второе записано теми же цифрами, что и первое, но в обратном порядке, быть квадратом натурального числа?»
Прежде чем решать эту задачу в общем виде, учащийся должен на частных примерах, с помощью неполной индукции, получить предполагаемый ответ (высказать гипотезу): рассматриваемая разность не может быть равна квадрату какого-либо натурального числа. Дедуктивное обоснование этой гипотезы, как правило, не вызывает у учащихся затруднений.
Учащиеся должны понимать. Что на частных примерах никакого утверждения доказать нельзя. Частный пример ничего не доказывает в математике, но он может подвести к правильному выводу.
Так, прежде чем предлагать учащимся задачу «Докажите, что из всех прямоугольников, имеющих данный периметр квадрат имеет наибольшую площадь», целесообразно рекомендовать им установить, как в зависимости от длин сторон изменяется площадь прямоугольника данного периметра. Пусть, например, периметр прямоугольника 40 см, длина одной из его сторон принимает (последовательно) значения 18. 16, 14, 10 см. Тогда длина другой стороны равна соответственно 2, 4, 6, 10 см, а его площадь – 36, 64, 84, 100 см². Таким образом, из всех рассмотренных прямоугольников наибольшую площадь имеет прямоугольник с равными сторонами, т.е. квадрат со стороной 10 см.
При отыскании различных способов решения задач у школьников формируется познавательный интерес, развиваются творческие способности, вырабатываются исследовательские навыки. После нахождения очередного метода решения задачи ученик, как правило, получает большое моральное удовлетворение. Поэтому учителю важно поощрять поиск различных способов решения задач, а не стремиться навязывать своё решение. Общие методы решения задач должны стать прочным достоянием учащихся, но наряду с этим надо воспитывать у них умение использовать индивидуальные особенности каждой задачи, позволяющие решить её проще. Именно отход от шаблона, конкретный анализ условий задачи являются залогом успешного её решения.
Особое внимание следует обращать на решение задач арифметическим способом, так как именно решение задач арифметическим способом способствует развитию оригинальности мышления, изобретательности.
Наблюдения показывают, что учащиеся, ознакомившись со способом решения задач с помощью уравнения, не обременяют себя глубоким анализом условия задачи, стараются побыстрее составить уравнение и перейти к её решению. При этом и введение обозначений, и схема решений, как правило, соответствует шаблону.
В этом случае задача учителя – показать учащимся на примерах, что решение задач по шаблону часто приводит к значительному увеличению объёма работы, а иногда и к усложнению решения, в результате чего увеличивается возможность появления ошибок. Поэтому учащимся полезно предложить, прежде чем, составлять уравнение для решения задачи, внимательно изучить условие задачи, подумать над тем, какой способ решения наиболее соответствует её условию, попытаться решить задачу без использования уравнений, арифметическим способом.
К сожалению, довольно широко распростраенено мнение, что решение задачи повышенной трудности арифметическим методом излишне, ввиду существования более сильного метода решения задачи с помощью составления уравнения.
Существует и другое мнение, опирающееся на наблюдения за учащимися, согласно которому решение задач только алгебраическим методом ведёт к одностороннему математическому развитию учащихся. Следует учитывать и то, что для составления уравнения требуются определённые арифметические навыки, понимание зависимостей между величинами. Кроме того, существует ряд задач, решение которых часто арифметическими методами изящнее и проще, чем с помощью уравнений.
Например, следующая задача: «Два мотоциклиста выехали одновременно из пунктов А и В навстречу друг другу и встретились в 50 км от В. Прибыв в пункт А и В, мотоциклисты повернули сразу же назад и встретились вновь в 25 км от А. Сколько километров от А до В?» Гораздо легче решить эту задачу, не составляя уравнения, а рассуждая так. От начала движения до первой встречи оба мотоциклиста проехали расстояние вместе, равное АВ, а к моменту второй встречи проехали вместе втрое большее расстояние. Таким образом, каждый из них до второй встречи проехал втрое больше, чем до первой. Мотоциклист, выехавший из пункта В, до первой встречи проехал 50 км. Следовательно, до второй встречи он проехал 150 км. Поэтому расстояние от А до В равно125 км.
Арифметический способ решения задач является одним из лучших средств самостоятельного творческого мышления учащихся. С помощью специально подобранных задач, которые способны заинтересовать учащихся своей кажущейся простотой и тем, что их решение не сразу даётся в руки, можно показать учащимся красоту, простоту и изящество логического рассуждения, приводящего к решению задачи.
Рассматривая решение задач несколькими способами, учитель на уроке и во внеклассной работе должен ориентировать учащихся на поиски красивых, изящных решений. Тем самым учитель будет способствовать эстетическому воспитанию учащихся и повышению их математической культуры.
Решая с учениками ту или иную задачу, учитель должен стремиться к достижению двух целей. Первая — помочь ученику решать им5нно данную задачу, научить его решать задачи, аналогичные рассматриваемой; вторая – так развить способности ученика, чтобы он в будущем смог решить любую задачу.
Поэтому, преследуя вторую цель, при решении задач несколькими способами следует обращать внимание учащихся не только на наиболее рациональный способ решения данной задачи, но и на те способы, которые широко применяются при решении других задач и в некоторых случаях являются единственными. Также частое применение одного и того же метода при решении задач иногда приводит к привычке, которая становится вредной. У решающего задачу вырабатывается склонность к так называемой психологической инерции. Поэтому, как бы не казался ученику простым найденный способ решения, всегда полезно попытаться найти другой способ решения, который обогатит опыт решающего задачу. Кроме того, в некоторых случаях получение того же результата другим способом служит лучшей проверкой правильности результата.
Как разобраться в любой задаче программирования
Джастин Фуллер
День, наконец, настал. Это ваш первый день на работе или вы занимаетесь им уже десять лет? Неважно. Все мы в конце концов сталкиваемся с задачей, которую просто не понимаем.
Так что же делать? Стоит ли просто начать и надеяться, что это сработает? Следует ли вам немедленно сказать своему начальнику, что вы не можете этого сделать, потому что не понимаете?
Я полагаю, что вы знаете, что ответ отрицательный!
В программировании, как и в любой другой профессии, я обнаружил, что почти невозможно прожить неделю (а иногда даже и день), не обнаружив какой-либо проблемы, которую я не понимаю.
Но не волнуйтесь! У меня отличные новости. Вы не только можете решить эту проблему, но и сделать это полезно.
Это означает, что вы каким-то образом расширяете свои навыки и знания за пределы того, что вы делали и знали раньше.
В следующих нескольких абзацах я подробно расскажу, как можно преодолеть разрыв между предъявляемыми к вам требованиями и знаниями, необходимыми для выполнения поставленной вам задачи.
О «требованиях»
Вы могли заметить, что я использовал слово «требования».Это слово может иметь определенный оттенок в зависимости от того, где вы работаете.
По моему опыту, большие компании любят требования, а маленькие компании иногда «не выполняют требований». Я думаю, что это идеально подходит для наших целей.
Это потому, что все, что мы делаем, как инженеры-программисты, — это решение проблем.
Вы можете получить обширный отчет на сто страниц о том, как решить эту проблему (однажды у меня было часовое совещание по поводу текста для кнопки).Или, может быть, ваш генеральный директор подойдет к вашему столу и небрежно спросит, сможете ли вы решить проблему к пятнице.
В любом случае — перед вами поставлена задача, и вам нужно быть уверенным, что вы полностью понимаете эту проблему, чтобы правильно ее решить!
.Как работают нестандартные опции?
Стандартный опцион на акции (известный как «обычная ванильная» или нескорректированная) требует поставки акций базовых акций и ничего другого; нет денежных средств, акций другой компании и т. д. Стандартный контракт предусматривает поставку 100 акций базовых акций; это число множитель .
Однако условия опционов на акции могут быть скорректированы группой, в которую входят Опционная клиринговая корпорация (OCC) и представители бирж опционов.Опционы на скорректированные акции — нестандартный вариант. Корректировки производятся в зависимости от ряда различных событий, таких как дробление акций, обратное дробление акций, крупные дивиденды, слияния, выделения и другие корпоративные события.
Целью корректировок является обеспечение того, чтобы продавцы и держатели опционов оставались как можно ближе к относительному экономическому положению, которое они занимали до события.
Нестандартные опционы колл могут потребовать поставки другого количества акций, поставки акций более чем одной компании или поставки базовых акций и денежных средств; пут-опционы требуют нестандартных покупок.

Креативность корпоративных участников сделок практически безгранична, и при корректировке опционов необходимо учитывать условия сделки; таким образом, мы иногда видим очень странные корректировки. Вот условия опциона, на которые может повлиять корректировка (срок действия не меняется):
- Множитель — количество акций, подлежащих поставке или приобретению по контракту
- Символ опциона
- — отсюда появляются нечетные страйки (например, 13,25 доллара) от
- Количество контрактов — да, это тоже может измениться
- Поставки — денежные средства, акции эмитента и акции другого эмитента могут быть поставлены
Страйк-цена
Корпоративные события, требующие корректировки — и какие изменения
Причины для корректировки условий стандартных опционных контрактов многочисленны.В следующей таблице показаны эффекты различных распространенных «корпоративных событий», таких как слияния, дробление акций и тому подобное. Нет необходимости запоминать эту таблицу (у нас нет), но помните о процессе, который OCC использует для обеспечения справедливости корректировок для всех сторон.
Рисунок 2.9
| Таблица: Опционные корректировки для корпоративных событий | |||||||
| Событие | Размер / Тип | Изменение символа | Изменения ударов | # Изменения контрактов | Множитель Изменения | Выплата наличными | Выпуск акций другого эмитента |
| Разделение запасов — даже | 2 для 1 3 для 1 4 для 1 5 для 1 | Нет Нет Нет Нет | Да; ▼ Да; ▼ Да; ▼ Да; ▼ | Нет Нет Нет Нет | Нет Нет Нет Нет | Нет Нет Нет Нет | Нет Нет Нет Нет |
| Разделение акций — нечетное, с наличными деньгами 1 | 3 для 2 4 для 3 5 для 4 5 для 5 7 для 5 | Да Да Да Да | Да; ▼ Да; ▼ Да; ▼ Да; ▼ Да; ▼ | Да; ▲ Да; ▲ Да; ▲ Да; ▲ Да; ▲ | Да; ▲ Да; ▲ Да; ▲ Да; ▲ Да; ▲ | Нет Нет Нет Нет Нет | Нет Нет Нет Нет Нет |
| Обратный раскол | 1 для 2 1 для 5 1 для 7 1 для 10 1 для 20 1 для 50 1 для 100 | Да Да Да Да Да Да Да | Да; ▼ Да; ▼ Да; ▼ Да; ▼ Да; ▼ Да; ▼ | Да; ▲ Да; ▲ Да; ▲ Да; ▲ Да; ▲ Да; ▲ | Нет Нет Нет Нет Нет Нет Нет | Нет Нет Нет Нет Нет Нет Нет | Нет Нет Нет Нет Нет Нет Нет |
| Дивиденды по акциям | Все | Есть | Да; ▼ | Да; ▲ | Да; ▲ | № | № |
| Дивиденды по обыкновенным денежным средствам 2 | Неважно | № | № | № | № | № | № |
| Внеочередные денежные дивиденды 3 | <12 долларов США.50 / к > $ 12,50 / к | Нет Нет | Есть | Нет Да; ▼ | Может быть | ||
| Слияние, акции | Приобретатель Приобретатель | Возможно Да | Нет Нет | Нет Да | Нет Нет | Может быть | Может быть |
| Передача прав | Есть | № | Да; ▲ | № | № | № | |
| Выделение | Есть | № | Да; ▲ | № | Может быть | Есть | |
| Биржевой символ или co.изменение имени | Может быть | № | № | № | № | № | |
| 1 Разделение нечетных запасов обычно сопровождается наличными, чтобы избежать нечетных долларовых сумм. 2 Выплачивается ежеквартально или на другой регулярной основе, независимо от суммы. 3 Регулярно не выплачивается. « K » означает договор. | |||||||
Как видите, единственным корпоративным событием, которое не влияет ни на одно из условий контракта, является получение обычных денежных дивидендов. Разделение акций (так называемое форвардное дробление) увеличивает количество акций в обращении на , разделяя их на большее количество акций.
Простым примером является дробление 2: 1 (2 к 1), при котором акции удваиваются: 100 акций превратятся в 200 акций. Разделение может включать простое дробление целых (четных), например 2: 1 или 3: 1 (держатели получают две или три акции на каждую принадлежащую им акцию ), или может включать нецелых ( odd) с разделением, например 3: 2 ( держателя получают 3 акции на каждые две принадлежащие им акции).
Разделение акций — четное
Когда деление составляет и даже , опцион разделяется так же, как и базовая акция, и аналогично страйк-цена — корректируются только страйк-цена и количество контрактов. Таким образом, при разделении 2: 1 вы получите вдвое больше опционов за половину цены исполнения; вариант страйка за 50 долларов превратится в два варианта по 25 долларов, но символы не изменятся.
Если бы вы написали 10 таких контрактов, после корректировки у вас были бы короткие 20 контрактов.Равномерное дробление акций, по-видимому, является единственным событием, в котором было выпущено дополнительных контракта на .
Изменения в забастовке | Выдано дополнительных контрактов
Разделение акций — Нечетное
Однако нечетных сплитов действительно может создать нечетные страйки. Если произойдет разделение 3: 1, вы получите в три раза больше контрактов (на каждый открытый контракт выдается два дополнительных контракта), а страйк-цены будут разделены на три и округлены в большую или меньшую сторону до ближайшей 1/8 ( например: 55 страйк становится 18-3 / 8) и не будет изменения символа.
Нечетное разделение обычно приводит к смене символа и «корректировке» цены и количества или количества поставляемых акций. Например, если BUMM разделится на 3 к 2 (3: 2), ваши опционы BUMM на 90 долларов будут скорректированы таким образом, чтобы они покрывали 150 акций по 60 долларов, а символ изменится.
Strike Changes | Изменения символов | Изменения множителя
Разделение акций — нечетное с наличной долей
Нечетные дробления с выплаченной долей наличных обрабатываются по-другому.Меняется символ, но не страйк или множитель, и деньги выдаются. Изменения символов | Денежный перевод
Обратный разделенный запас
При обратном дроблении акций (комбинация) количество акций в обращении составляет , уменьшено путем объединения их в меньшее количество акций.
Таким образом, при обратном дроблении 1: 4 (1 к 4) каждые четыре акции, принадлежащие акционеру, будут объединены только в одну акцию, и тот, кто владеет 100 из этих акций, увидит, что они превратятся только в 25 акций.
При обратном разделении цена страйка не меняется, но меняется символ и множитель. Если гипотетическая акция BUMM подвергнется обратному разделению 1: 4, страйки останутся такими же, но символы изменятся, и только 25 акций будут доступны.
Изменения символов | Изменения множителя Дивиденды по акциям
Дивиденды , наличными или акциями, , как правило, приводят к корректировке опционов только в том случае, если они превышают 10% стоимости акции (денежные средства) или увеличивают количество находящихся в обращении акций более чем на 10% (акции).В случае корректировки денежного дивиденда цена исполнения опциона будет уменьшена на сумму денежного дивиденда. Однако на практике особые дивиденды в размере даже около $ 1, кажется, приводят к корректировке цены исполнения. Например, дивиденды Saks за 2006 год в размере 4 долларов на акцию снизили цену исполнения на те же 4 доллара. Тем не менее, для выплаты дивидендов OPWV в размере 1,20 долл. США за 2007 г. потребовалось дополнительно 120 долл. США за контракт, без изменения забастовки.
Strike Изменения
Дивиденды по акциям, превышающие 10%, рассматриваются как дробления акций .Например, дивиденд в размере 10% по акциям, при котором одна новая акция выпускается на каждые 10 акций, находящихся в обращении, в действительности является дроблением 11:10. Если производится корректировка для денежного дивиденда, цена исполнения опциона будет уменьшена на сумму дивиденда, а символы изменятся. Если требуется корректировка, она выполняется так же, как при разделении запасов.
Слияние, Акции
При типичном слиянии приобретаемая корпорация (исчезающая компания) сливается с приобретающей компанией; это сценарий « слияния равно ».Опционы исчезающей компании обычно требуют после даты вступления в силу слияния поставки или покупки акций покупателя, возможно, с внесением денежной суммы.
Изменения символов | Множитель может измениться | Возможно размещение акций другого эмитента | Также могут потребоваться наличные
Слияние, обналичивание
При слиянии с выплатой наличных акционеры исчезающей компании получают только наличные деньги, таким образом, только сумма наличных должна быть выплачена от (к) автору колл (писатель пут) при назначении.Вариантом является слияние на выборах , в котором акционеры исчезающей компании могут выбрать, хотят ли они акций или денежных средств, как в случае слияния Veritas / DGC в 2006 году. В таком случае вместо акций могут быть предоставлены денежные средства. Денежные средства доставлены
Выделение дочерней компании
Выделение происходит, когда одна корпорация полностью или частично владеет другой (дочерней компанией) и распределяет среди своих акционеров все или часть принадлежащих дочерней компании акций.Опционы на компанию, осуществляющую распределение, требуют поставки или покупки акций распределительной компании и акций выделяемой дочерней компании.
Изменения символов | Выпуск акций другого эмитента
Тендерное предложение
Опционы не корректируются для отражения предложения на торгах за денежные средства. (выкуп), даже если тендерное предложение может иметь положительное или отрицательное влияние на выставляемые на торги акции, исходя из теории, что ни цена исполнения, ни множитель (количество акций) результат по контракту) изменяются.Часто тендер является частичным, обычно в рамках самотендера , в котором корпорация выставляет свои собственные акции. То же самое должно относиться к выкупу акций под руководством руководства.
> Когда рухнет фондовый рынок?
> Почему больше людей не пишут обслуживаемые звонки?
# 1 Акция на следующие 7 дней
Когда Financhill опубликует свои акции №1, слушайте. В конце концов, акции №1 — лучшие из лучших, даже когда рынки рушатся.
Financhill только что представила инвесторам свои лучшие акции … так что сейчас самое время забрать свой кусок пирога.
Смотрите сейчас # 1 на складе >>
Автор не имеет позиций ни по одной из указанных акций. Financhill придерживается политики раскрытия информации. Этот пост может содержать партнерские ссылки или ссылки от наших спонсоров.
.
Страница не найдена · GitHub Pages
Страница не найдена · GitHub Pages
Файл не найден
Сайт, настроенный по этому адресу, не
содержать запрошенный файл.
Если это ваш сайт, убедитесь, что регистр имени файла соответствует URL-адресу.
Для корневых URL (например, http://example.com/ ) вы должны предоставить
index.html файл.
Прочтите полную документацию
для получения дополнительной информации об использовании GitHub Pages .
.
Основные типы информационных задач и некоторые методы их решения | Материалы Международной конференции по научной информации: два тома
памяти (16), а также выделить часть этого устройства для записи промежуточных результатов анализа и программы его выполнения. Таким образом, решение задач IV типа в целом требует применения современных универсальных или даже специальных цифровых вычислительных машин. Следует, однако, отметить, что в настоящее время существует лишь очень мало информационных задач, в которых приближение e k и вопросы могут быть выполнены однозначно с такой большой точностью. и сложность, требующая решения этих задач с помощью таких усовершенствованных устройств.
ССЫЛКИ
1. В.П. ЧЕРЕНИН, Некоторые проблемы документации и механизации информационных поисков, , М., 1955.
2. БМРАКОВ, ВПЧЕРЕНИН, Экспериментальная информационная машина Института научной информации АН СССР , Москва, 1955 (есть также публикация на английском языке). язык).
3. Дж. У. ПЕРРИ, А. КЕНТ, М. М. Берри, Поиск литературы по машинам , Interscience, Нью-Йорк-Лондон, 1956.
4. W.C.ADAIR, Указатели цитирования научной литературы? Американская документация , 6, [1], 1955.
5. Б. К. ВИКЕРИ, Развитие предметной индексации, The Journal of Documentation , 11 , [1], 1955.
6. Б.М.РАКОВ, В.П.ЧЕРЕНИНА, Бюллетень ЮНЭСКО для библиотеки; Машины для сбора информации в СССР, Бюллетень библиотеки ЮНЕСКО , 11 , [8–9], 1957. (Также опубликовано на английском, французском и испанском языках; статья перепечатана на немецком языке) язык в журнале Nachrichten fur Dokumentation , 9 [1], 1958.
7. Э.А.АВАКЯН, Э.ГАРФИЛД, AMFIS — Автоматическая информационная система для микрофильмов, Специальные библиотеки , апрель 1957 г.
8. M.TAUBE and ASSOCIATES, Исследования по индексированию координат , Vol. I, 1953.
9. То же, Vol. II, 1954.
10. То же, Vol. III, 1956.
11. Р.С. КЕЙСИ, Дж. У. ПЕРРИ, Перфокарты — их применение в науке и промышленности , Reinhold, New York, 1951.
12. J.SAMAIN, Filmorex— Новая методика классификации и выбора документов и информации , Paris, 1952.
13. J.W.PERRY and ALLEN KENT, Das lesende Selektiongerät der Western Reserve University, Nachrichten für Dokumentation , No. 2, 1957.
14. А. В. ТАЙЛЕР, В. Л. Майерс, Дж. В. Кайперс, Применение системы мини-карт Kodak к проблемам документации, American Documentation , 6 , [1] , 1955.
15. А.ОПЛЕР, Т.Р. НОРТОН, Новая скорость структурных поисков, Chemical and Engineering News , 4 июня 1956 г.
16. W.H.T. Дэвисон и М.Гордон, Сортировка по химическим группам с использованием шифров Гордона-Кендалла-Дэвисона, American Documentation , 8 , [3], 1957.
.

