Рациональный способ: Рациональные приёмы вычислений на уроках математики
Рациональные приёмы вычислений на уроках математики
«Мозг хорошо устроенный ценится больше,
чем мозг хорошо наполненный.»
Умения рационально производить вычисления характеризуют довольно высокий уровень математического развития. Знакомство и применение рациональных способов вычислений развивает вариативность мышления, показывает ценность знаний, которые при этом используются. Эти умения чрезвычайно сложны, формируются они медленно и за время обучения в начальной школе далеко не у всех детей могут быть достаточно сформированы.
Говорят, если хотите научиться плавать, вы должны войти в воду, а если хотите уметь решать задачи, то должны начать их решать. Но для начала надо освоить азы арифметики. Научиться считать быстро. Считать в уме можно только при большом желании и систематической тренировки. И тогда перед вами откроется совсем другая математика: живая, полезная, понятная.
Начнём открывать.
Скажите, пожалуйста, как рациональнее сложить 1+ 7, 4 * 8? Какие законы применили?
27 + 46+13? 27 – 19 – 7? Какие свойства, законы? Т.е основы рациональных приёмов вычислений основаны на чём?
Методика преподавания математики в начальных классах раскрывает основы рациональных приёмов вычислений, связанных с выполнением разных математических действий с натуральными числами.
Рациональные приёмы сложения основываются
1. Коммуникативный закон сложения а +в =в +а
2. Ассоциативный закон сложения а+в+с = а+ (в+с)
на коммуникативном и ассоциативном приёмах сложения, а так же свойствах изменения суммы. Рассмотрим некоторые из них.
Свойства сложения.
1.1
а+в+с =У, то (а – к) +с+в = У –к
38+24+15 = 77, то 36+ 24+ 15 = ?
а+в+с=У, то (а+ к) +в +с = У+к
38 + 24+15 = 77, то 40+ 24 + 15 =?
1.2.
а+ в =С , то (а +к ) + (в – к) = С
56 + 27 = 83, то (56 + 4) + (27 – 4) = ?
Какие ещё рациональные приёмы сложения можно применить на уроке математики?
Округление одного из слагаемых; поразрядного сложения; приём группировки вокруг одного и того же «корневого» числа.
Рассмотрим эти приёмы:
13 + 49 + 76 + 61 = (поразрядное сложение)
38 + 59 = 38 + (…округление слагаемого)
26 + 24 + 23 +25 + 24 = (группировка вокруг одного и того же «корневого» числа
Все приёмы рациональных вычислений, связанных с вычитанием, основываются на законах вычитания.
Если уменьшаемое увеличить или уменьшить на число, то соответственно разность увеличится или уменьшится на это же самое число
а – в = С, то (а +к) — в = С +к
74 – 28 = 46, то 77 – 28 = 49
а-в = С , то (а – к ) — в = С-к
74 – 28 = 46, то 71 – 28 = 43
Если вычитаемое увеличить или уменьшить на несколько единиц, то разность измениться в противоположную сторону.
Если уменьшаемое и вычитаемое уменьшить или увеличить на одно и тоже число, то разность не измениться.
Найди верные равенства.
229 – 36 = (229 – 9 ) – ( 36 – 6)
174 – 58 = (174 – 4) – ( 58 – 4)
358 – 39 = ( 358 – 8 ) – (39 – 8)
617 – 48 = ( 617 – 7 ) – (48 – 8)
Для рациональных вычислений используют частичные приёмы умножения и деления.
Приём замены множителя или делителя на произведение.
75 * 8 = 75 * 2*2*2=
960 : 15 = 960 : 3 : 5 =
Приём умножения на 9, 99,999, 11 …
87 * 99 = 87 * 100- 87 = 8700 – 87 = 8613
87 * 11 = 87 *10 + 87 = 870+ 87 = 957
Успешное применение различных приёмов зависит от умения подмечать особенности чисел и их сочетаний. Например, познакомив детей в первом классе с натуральным рядом чисел и имея его перед глазами, легко закрепить состав числа.
0 1 2 3 4 5 6 7
Отработав, таким образом, состав чисел в пределах 10 и познакомившись с переместительным законом сложения, дети легко справляются с заданием найти сумму чисел в пределах 10, а в дальнейшем, используя переместительное и сочетательное свойство сложения, легко можно найти сумму других чисел. Например:
48 +14 +22 +36 =120
Существуют приёмы на знаниях некоторых свойств чисел или результатов действий. Легко находить сумму последовательных нечётных чисел, начиная с 1.
Она равна произведению количества слагаемых на самого себя.
(проверить)
Рационализация может осуществляться за счет возможности выполнять некоторые арифметические действия. Для этого очень важно научить детей внимательно рассматривать условия задания, суметь подметить все его особенности. Такие задания, как поставь нужный знак действия16 … 17 = 33 ( рассуждать), далее подобные задания усложняются. 8…6…33 = 15
Сравни, не вычисляя
2+2+2 … 2*3
51 : 3 … 30 : 3 + 21 :5
636 :6 … 600 : 6+ 30 : 6+ 6 :6
Задания могут даваться в занимательной форме: Математический лабиринт, составь слово, найди пару , расшифруй пословицу и т.д.
Используй рациональные приёмы вычисления, разгадай слово
| 18 *9 = | 24 +29 = | 21 *11= |
53 – М | 162 – И | 231 – Р |
Какие приёмы использовали?
Важно показать ученикам красоту и изящество устных вычислений, используя разнообразные вычислительные приёмы, помогающие значительно облегчить процесс вычисления.
СЧЁТ НА ПАЛЬЦАХ: способ быстрого умножения чисел первого десятка на 9. Допустим нам надо умножить 7 на 9. Повернём ладошки к себе, загнём седьмой палец, число пальцев слева от загнутого пальца – это число десятков, а число – справа, количество единиц.
Все задания, которые рассматривались, воспитывают интерес к математике, развивают их математические способности. Такую работу можно продолжать на математическом кружке.
Приложение
Знаете ли вы, что значит «рациональный» и какие числа называются рациональными?
В далеком прошлом, когда еще не была придумана система исчисления, люди подсчитывали все на пальцах. С появлением арифметики и основ математики стало гораздо проще и практичнее вести учет товаров, продуктов, а также бытовых предметов. Однако как выглядит современная система исчисления: на какие виды делятся существующие числа и что значит «рациональный вид чисел»? Давайте разберемся.
Сколько разновидностей чисел существует в математике?
Само понятие «число» обозначает некую единицу любого предмета, которая характеризует его количественные, сравнительные или порядковые показатели. Для того чтобы правильно подсчитать количество определенных вещей или провести некие математические операции с числами (сложить, умножить и др.), в первую очередь следует ознакомиться с разновидностями этих самых чисел.

Итак, существующие числа можно разделить по следующим категориям:
- Натуральные — это те числа, которыми мы подсчитываем количество предметов (самое меньшее натуральное число равно 1, логично, что ряд натуральных чисел бесконечен, т. е. не существует наибольшего натурального числа). Множество натуральных чисел принято обозначать буквой N.
- Целые числа. К этому множеству относятся все натуральные числа, при этом в него добавляются и отрицательные значения, включая число «ноль». Обозначение множества целых чисел записывают в виде латинской буквы Z.
- Рациональные числа — это те, которые мы мысленно можем преобразовать в дробь, числитель которой будет принадлежать множеству целых чисел, а знаменатель — натуральных. Чуть ниже мы разберем подробнее, что значит «рациональное число», и приведем несколько примеров.
- Действительные числа — множество, в которое входят все рациональные и иррациональные числа. Обозначается данное множество буквой R.
- Комплексные числа содержат в себе часть действительного и часть переменного числа. Используются комплексные числа в решении различных кубических уравнений, которые, в свою очередь, могут иметь в формулах под знаком корня отрицательное выражение (i2= -1).
Что значит «рациональный»: разбираем на примерах
Если рациональными считаются те числа, которые мы можем представить в виде обыкновенной дроби, то получается, что все положительные и отрицательные целые числа также входят в множество рациональных. Ведь любое целое число, например 3 или 15, можно представить в виде дроби, где в знаменателе будет единица.
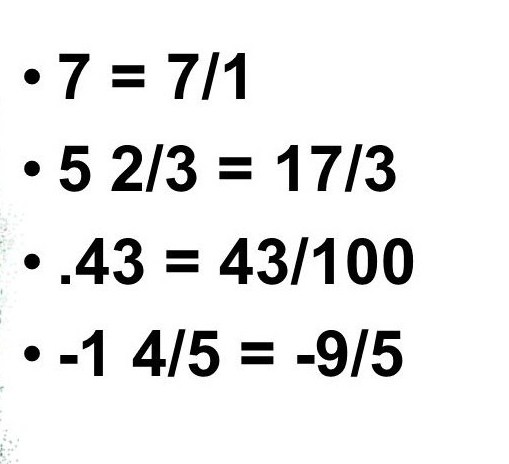
Дроби: -9/3; 7/5, 6/55 — вот примеры рациональных чисел.
Что значит «рациональное выражение»?
Идем дальше. Мы уже разобрали, что значит рациональный вид чисел. Давайте теперь представим себе математическое выражение, которое состоит из суммы, разности, произведения или частного различных чисел и переменных. Вот пример: дробь, в числителе которой сумма двух или нескольких целых чисел, а знаменатель содержит в себе как целое число, так и некую переменную. Именно такое выражение и называют рациональным. Исходя из правила «на ноль делить нельзя» можно догадаться, что значение данной переменной не может быть таковым, чтобы значение знаменателя обращалось в ноль. Поэтому при решении рационального выражения следует сначала определить область значения переменной. Например, если в знаменателе следующее выражение: x+5-2, то получается, что «x» не может быть равен -3. Ведь в таком случает все выражение превращается в ноль, поэтому при решении необходимо исключить целое число -3 для данной переменной.

Как правильно решать рациональные уравнения?
Рациональные выражения могут содержать в себе довольно-таки большое количество чисел и даже 2 переменные, поэтому порой их решение становится затруднительным. Для облегчения решения такого выражения рекомендуется произвести некие операции рациональным путем. Итак, что значит «рациональным способом» и какие правила необходимо применять при решении?
- Первый вид, когда достаточно всего лишь упростить выражение. Для этого можно прибегнуть к операции сокращения числителя и знаменателя до несокращаемой величины. Например, если в числителе имеется выражение 18x, а в знаменателе 9х, то, сокращая оба показателя на 9x, получаем просто целое число, равное 2.
- Второй способ практичен тогда, когда в числителе имеем одночлен, а в знаменателе — многочлен. Разберем на примере: в числителе имеем 5x, а в знаменателе — 5x + 20x2. В таком случае лучше всего вынести переменную в знаменателе за скобки, получим следующий вид знаменателя: 5x(1+4x). А теперь можно воспользоваться первым правилом и упростить выражение, сократив 5x в числителе и в знаменателе. В итоге получим дробь вида 1/1+4x.

Какие действия можно выполнять с рациональными числами?
Множество рациональных чисел имеет ряд своих особенностей. Многие из них весьма схожи с характеристикой, присутствующей у целых и натуральных чисел, ввиду того что последние всегда входят в множество рациональных. Вот несколько свойств рациональных чисел, зная которые, можно с легкостью решить любое рациональное выражение.
- Свойство коммутативности позволяет суммировать два или несколько чисел, вне зависимости от их очередности. Проще говоря, от перемены мест слагаемых сумма не меняется.
- Свойство дистрибутивности позволяет решать задачи с помощью распределительного закона.
- И, наконец, операции сложения и вычитания.
Даже школьники знают, что значит «рациональный вид чисел» и каким образом решать задачи на основе таких выражений, поэтому взрослому образованному человеку просто необходимо вспомнить хотя бы азы множества рациональных чисел.
Предложения со словосочетанием РАЦИОНАЛЬНЫЙ СПОСОБ
Познавательный интерес — важнейшее условие успешной учебной работы младшего школьника, быстрого и прочного усвоения им учебного материала и рациональных способов работы с ним.
Самый рациональный способ — вытянуть навстречу мячу разведённые по его окружности пальцы.
На этапе двигательных умений создаётся широкое предметное поле для проявления интеллектуальных способностей, совершенствующих качественные параметры деятельности, поскольку в основу двигательного умения заложен творческий поиск наиболее рациональных способов исполнения движений, что способствует использованию подростком образовательных возможностей спортивной деятельности.
Такая работа над составлением плана воспринятого текста оказывается очень полезной не только для его запоминания, но и для выработки рационального способа умственной деятельности вообще.
Для успешной реализации разрабатываемой промо-программы необходимо определить самый рациональный способ донесения информации до целевого рынка.

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать
Карту слов. Я отлично
умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.
Насколько понятно значение слова раззвонить (глагол), раззвонил:
Кристально
понятно
Понятно
в общих чертах
Могу только
догадываться
Понятия не имею,
что это
Другое
Пропустить
Самый рациональный способ сосуществования разнообразного мира — учесть интересы каждой группы людей.
Актуальность поставленных задач исследования определяется тем, что, как известно из сурдопсихологии, глухие учащиеся часто затрудняются в соотнесении стоящей перед ними цели действий, условий и рациональных способов их осуществления.
В дальнейшем человечество стало использовать более рациональные способы борьбы со старением, в основном связанные с разумным управлением своим здоровьем и продолжительностью жизни.
Гражданское общество в современном его понимании представляет собой необходимый и рациональный способ сосуществования людей, основанный на разуме, свободе, праве и демократии при разумно необходимом вмешательстве государства.
Ознакомление с приёмом направлено на формирование у обучаемых целостного представления об изучаемом приёме, о наиболее рациональных способах его выполнения.
У нас есть рациональные способы возвращать весь навоз на поля.
Таким образом, важнейшей особенностью эволюционного процесса является противоречивое взаимодействие тенденций двух различных типов — тенденций к стабильности, нуждающийся в укреплении отрицательных обратных связей, и тенденций поиска новых, более рациональных способов использования внешних энергии и вещества, необходимо требующих формирования положительных обратных связей и ограничения стабильности.
Таким образом, одной из важнейших особенностей любого эволюционного процесса, протекающего в живом мире, является противоречивое взаимодействие тенденций двух противоположных типов — тенденции к стабильности (сохранению гомеостазиса), нуждающиеся в укреплении отрицательных обратных связей, и тенденции поиска новых, более рациональных способов использования внешней энергии и вещества, требующих формирования положительных обратных связей.
Это был бы разумный и вполне рациональный способ действий — пусть даже во всём происходившем не чувствовалось ничего разумного и рационального.
Следует заметить, что эмпиризм, по исходному замыслу отвергающий рациональный способ познания как частью схоластический и препятствующий постижению вещей в их «таковости» на основе чувственного опыта, в самой систематике несёт явный отпечаток рационализма.
Таким образом, предметом спортивной экономики как научной дисциплины является проблема выбора наиболее рациональных способов потребления ресурсов (факторов производства) для расширения рынка производимых услуг, максимального приближения их ассортимента и качества к потребительским запросам.
Федотовой, овладение подобным пространством позволяет школьникам наиболее рациональным способом освоить окружающую среду.
А неприятие рациональных способов объяснения сакральных истин и вместе с тем неудовлетворённость догматической замкнутостью раввинистического иудаизма способствовали, в свою очередь, усилению мистических тенденций в иудаизме.
И ещё — нашла не совсем рациональные способы решения задач.
Кроме того, принадлежность к новым высшим разрядам определялась в зависимости от получаемого ежегодного дохода с земельного участка, а это вынуждало его владельца изыскивать более рациональные способы обработки земли для получения большего урожая.
Учитель сначала демонстрирует ребёнку рациональный способ работы с материалом, а затем даёт ему возможность заниматься самостоятельно.
Для выполнения этих построений целесообразно выбирать рациональный способ выполнения чертежа.
Выбор рационального способа решения задачи сокращает время, затрачиваемое на работу.
Упражнение 6. Разделите окружность на восемь равных частей наиболее рациональным способом.
Выбор рациональных способов расшлихтовки определяется составом шлихты и природой волокнистого материала.
Его принятие должно основываться на выборе наиболее рационального способа достижения поставленной цели, механизма её достижения, построении соответствующей информации.
Древнее человечество, используя появившиеся у него способности, разрабатывало всё более и более рациональные способы производства, благодаря чему смогло мигрировать далеко за пределы джунглей и саванн.
Рациональный способ восприятия — состояние прозрачной проточной воды.
Метафизический принцип не может быть постигнут рациональными способами — по причине их обусловленности временем и, следовательно, не подходящих для понимания того, что является вечным.
Стоит отметить, что самым рациональным способом общения между людьми в служебной обстановке являются непосредственные устные контакты и телефонные разговоры.
Силы в борьбе прилагаются посредством «рычагов», обеспечивающих рациональный способ выполнения приёма.
Сортировка «рутины», находящейся в папке или лотке для входящих документов, является самым рациональным способом формирования правильного подхода ко всему новому, что поступает из окружающего мира.
Затем вернитесь назад и найдите более взвешенный и рациональный способ решения возникшей проблемы.
Необходимо выделить его огромное самообладание и уверенность, которые в, казалось бы, безнадёжной обстановке позволяли применить наиболее рациональные способы решения поставленных задач.
Ещё недавно отсутствие технической возможности выявления подходящих людей для выработки решений вынуждало правительство опираться на мнение ограниченного круга профессионалов, что было наиболее рациональным способом снизить стоимость поиска необходимых для государственного управления компетенций.
Соединение точечных частиц вещества, каждой с каждой, отрезками материальных (реально существующих) одномерных линий, наделённых силовыми свойствами и возможностью пересекаться между собой без разрушения, является наиболее простым и рациональным способом обеспечить взаимодействие между ними.
Соответственно, наиболее простым и рациональным способом обеспечить существование материи в движении и во времени, можно считать неразрывную структуру, состоящую из дискретных элементов упругой одномерной не имеющей массу материи, связанных между собой в узловых точках, наделённых инертностью (массой) и вообще не имеющих объём (пространственную размерность).
Хладнокровная проверка на оселке строгой логики устанавливает непригодность рациональных способов для того, чтобы обрести подобное метафизическое освящение каждой отдельной жизни.
Управленческая функция социологии заключается в нахождении рациональных способов решения конкретных общественных проблем на настоящем этапе, а также проблем, которые могут возникнуть в результате определённых управленческих воздействий в будущем.
Соответственно преобладание того или иного типа мышления определяет склонность человека к художественному или рациональному способу восприятия мира.
Они оптимизируют деятельность человека, вооружают его наиболее рациональными способами организации деятельности.
Деятельность детей на занятиях направлял воспитатель, который не только должен был передать им знания и умения, но и обучить наиболее рациональным способам их усвоения.
Ну что же, это вполне рациональный способ, позволяющий легко закрепить границы в математической форме.
Взаимная кооперация видится ими как рациональный способ и укрепления конкурентных преимуществ над общими соперниками, и нейтрализации взаимной конкурентной активности.
Само же поведение, точнее, его сущность, раскрывается в процессе поиска наиболее рационального способа взаимодействия со средой.
Иными словами, люди обнаружили, что самый древний образ жизни — натуральное хозяйство (когда семья производит все блага для себя сама) — не самый рациональный способ обеспечения благосостояния.
Рациональный способ познания мира привёл к переосмыслению всего комплекса накопленных ранее сведений, главной задачей которого стала их систематизация во всех областях знания.
Неточные совпадения
Сущность данного способа состоит в рациональном расчленении деятельности на процедуры и операции с их последующей координацией и синхронизацией.
Использование термина «подход» позволяет снять характерные для российской концепции толкования терминологические споры о соотношении способов, методов и приёмов толкования закона, сфокусировавшись на поиске рациональных возможностей в процессе интерпретации.
Бывает и так, что у нас не получается полностью объяснить действие таким способом, поскольку мы не можем увидеть в этом действии продукт рационального рассуждения с достаточными предпосылками и соответствующим им заключением, и тогда, по всей видимости, нам понадобится каузальное объяснение.
Интеллектуальное сознание, или интеллект, выступает в качестве объекта и, одновременно, инструмента теории познания и представляет собой способность человека к рациональной познавательной деятельности, реализует его стремление к адекватному отражению истинной картины окружающего мира и законов его развития в своём сознании, к пониманию им собственной сущности и своего места в мире, а также способов осуществления своей жизнедеятельности.
Развитие способов использования стратегических ресурсов, технологический и научный прогрессы, освоение новых сегментов рынка предполагают разработку универсальных методов рационального их использования с учётом интересов отдельных государств, в том числе в спектре их сотрудничества на международном уровне.
Поэтому философия нового времени представляет собой процесс острых дискуссий и борьбы сенсуализма и рационализма, индуктивного и дедуктивного способов познания, столкновения эмоционального и рационального в осмыслении самой сущности человека.
Недостаток сил авиации в обороне предполагалось компенсировать рациональным выбором задач, применением эффективных способов их выполнения, массированием усилий, высокой активностью и решительностью действий авиации (главным образом — истребительной и штурмовой) при их осуществлении.
При первом способе мы начинаем сознательно или неосознанно объяснять себе, что «абдрапапупа — это то, чем рисуют на бумаге», пытаясь таким способом образовать рациональную связь «абдрапапупа — бумага».
Операциональная готовность рассматривается как комплекс способностей, позволяющих юному спортсмену совершать рациональный, адекватный выбор необходимых операций и видов действий, самостоятельно определять характер комплексирования технических элементов по выполнению двигательной и собственно интеллектуальной задачи из её элементов, находить методики достижения цели уже имеющимися в опыте спортсмена или вновь созданными способами.
Этот классический способ освоения мира характеризуется рациональным постижением истины, что существенно отличает его от восточной мудрости.
Мы считаем, что такой способ обслуживания более рациональный.
Перечень требований к лечебному (диетическому) питанию совпадает с таковым для рационального питания, однако с учётом характера заболевания на короткий или продолжительный срок могут изменяться требования к энергетической ценности и химическому составу рациона, сбалансированности в нём пищевых веществ, набору продуктов и способам их кулинарной обработки, некоторым органолептическим показателям пищи, режиму питания.
Нет никакого способа решить этот вопрос, кроме попытки выработать критерии, позволяющие определить, когда индивид может и должен с рациональной точки зрения отвечать за свои поступки, а затем использовать эти критерии для корректировки реактивных установок.
Биоцентристы представляют жизнь человека в природе как определённый способ бытия и тип поведения, когда охрана природы и рациональное природопользование могут быть лишь внешними проявлениями более глубоких мотивов и ценностных ориентаций.
Экономическое же содержание заключается в изготовлении изделия наиболее рациональным и эффективным способом.
Это непрерывный процесс, заключающийся в поиске, обосновании и реализации наиболее рациональных методов, способов и приёмов обеспечения безопасности, своевременном выявлении потенциальных угроз безопасности объекта.
Результатом такого поиска является система социально апробированных принципов и способов рационального познания политической действительности, правил и нормативов построения политической теории и образцов организации практической политической деятельности.
Как уже говорилось, книга написана в подчёркнуто «разъясняющей» манере (в духе рациональной терапии): последовательно и подробно описываются типичные ошибки, предубеждения и стереотипы, предлагаются способы их предупреждения.
После второй мировой войны одним из основных источников контркультурного движения были восточные религиозно-философские учения (как основания для получения внеязыкового опыта, отличного от существующего на западе способа неагрессивного решения конфликтов, формирования целостной картины мира без логического, рационального его осмысления) и поиски нового культурного опыта через употребление наркотических средств.
определение, значение и этапы решения
Рациональное принятие решений — это очень здорово и интересно. Прочтите наше полное руководство по производительности здесь, чтобы получить дополнительные советы по повышению производительности труда. Но прежде чем мы изучим каждый шаг этого мощного процесса, давайте рассмотрим, что такое рациональное принятие решений и почему это важно.

Вопросы и ответы
Чтобы точно определить вашу конкретную проблему, соберите как можно больше данных в нужной области и проанализируйте их, чтобы найти какие-либо тревожные закономерности или тенденции.
Пример: «Проанализировав наш отчет о трафике блога, мы теперь знаем, почему он за последние годы резко упал: наш органический трафик немного увеличивается по сравнению с предыдущим месяцем, а электронный и социальный — уменьшаются».
Другие решения
Потенциальное решение: «Мы могли бы сосредоточиться исключительно на растущем почтовом трафике: он легче, чем растущие социальный и органический одновременно. У нас также есть 250 000 подписчиков блога, поэтому мы могли бы публиковать наши сообщения для множества читателей».

Потенциальный результат 1: «Увеличение трафика электронной почты за счет отправки двух писем в день подписчикам нашего блога является сложной задачей, потому что мы уже отправляем одно письмо подписчикам ежедневно и на канал приходится только 15 % нашего трафика блога. Сосредоточение на электронной почте даст минимальные результаты». Рациональные решения проблем — это очень важно. Без них ни одна компания не может работать. Точно так же без этой способности не может существовать ни один человек, потому что это ключевой успех нашего сознания, отрицать который невозможно. В дальнейшем по всей статье вы найдете реальные примеры того, насколько это важно и интересно. Без этого никак нельзя строить бизнес. Мыслить рационально не только полезно и необходимо, но и в некотором роде приятно. Это может подтвердить любой человек, который либо занимается десижн-мейкингом на профессиональном уровне, либо просто ведет очень уравновешенную жизнь.
Потенциальный результат 2: «Увеличение органического трафика за счет ориентации на ключевые слова с большим объемом поиска для всех наших новых сообщений — самый простой способ увеличить общий трафик нашего блога. У нас высокий авторитет в области доменов, Google использует 80 % нашего общего трафика, и мы только что внедрили модель с кластером столбов. Сосредоточение внимания на органике дало бы большинство результатов».

Пример: «После месяца тестирования трафик нашего блога вырос на 14 %, а органический — на 21 %».
Важные примеры
Люди ассоциируют с брендами те же черты личности, что и с людьми: выбор любимого бренда — это выбор лучшего друга или другого человека. Мы идем с опцией, которая заставляет нас чувствовать что-то. Решение рациональных неравенств — это лучший способ изучения таких феноменов, как популярность брендов, изменение запросов клиентов и так далее.
Почему все так?
Модель рационального планирования используется при планировании и проектировании микрорайонов, городов и регионов. Она была центральной в развитии современного городского и транспортного планирования. Модель имеет много ограничений, связанных, в частности, с отсутствием руководства по вовлечению заинтересованных сторон и сообщества, затронутого планированием. Другие модели планирования, такие как совместное планирование, в настоящее время также широко используются. Решение рациональных уравнений (8 класс) — очень популярный метод в школе.
Другие модели
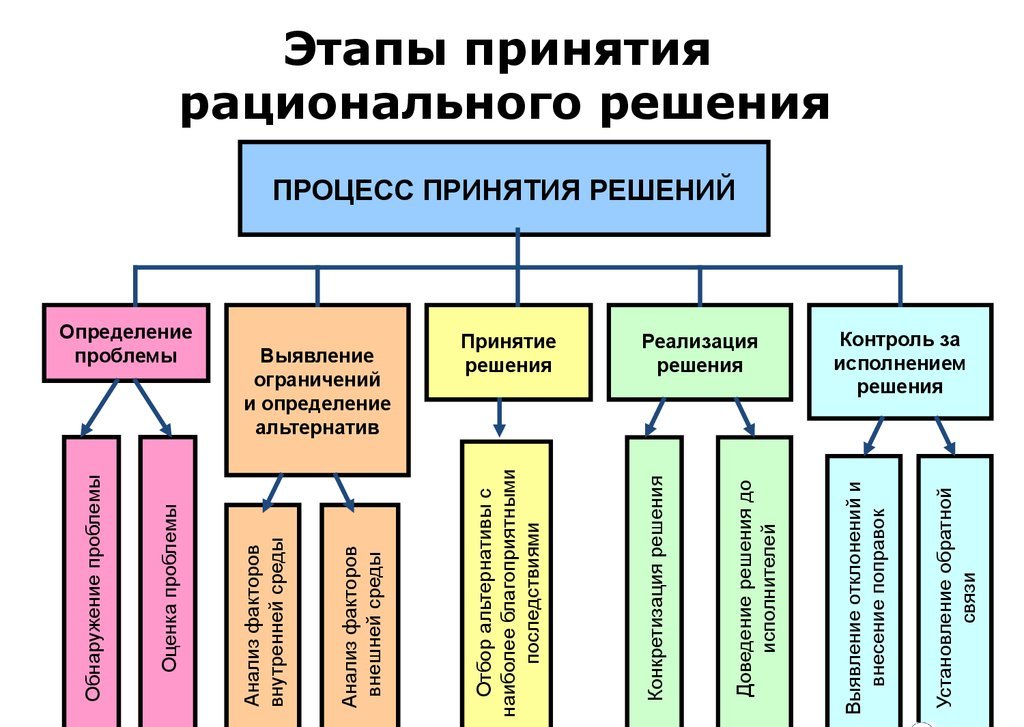
Очень похожая модель рационального принятия решений, как ее называют в организационном поведении, представляет собой весьма интересный процесс. Ему посвящена значительная часть этой статьи. В сущности, она заключается в принятии логически обоснованных решений. Это многошаговая модель, которая стремится быть логичной и следовать упорядоченному пути. Рациональное принятие решений — это многоэтапный путь к логически обоснованному выбору.
Первый шаг — это проверка, определение и детализация проблемы (определение проблемы, определение цели, сбор информации). Он включает в себя распознавание проблемы, выбор первоначального решения и запуск первичного анализа. Примерами этого являются творческие разработки и идеи, вдохновение, прорывы и мозговые штурмы.

Самый первый шаг, который обычно игнорируется руководством высшего уровня, — это определение точной проблемы. Хотя считается, что выявление проблемы очевидно, во многих случаях это не так. Рациональная модель принятия решений — это процесс принятия решений на основе групп. Если проблема не идентифицирована должным образом, то можно столкнуться с трудностями, поскольку у каждого члена группы может быть свое определение ее.
Этот шаг включает в себя два-три окончательных решения проблемы и предварительную реализацию сайта. При планировании примерами этого являются плановые единицы развития и оживления в центре города.
Это упражнение лучше всего выполнять в группах, так как разные люди могут предлагать разные идеи или альтернативные решения. Без них есть шанс прийти к неоптимальному или рациональному решению. Для изучения альтернатив необходимо собрать информацию. Технология может помочь в ее сборе.
Оценочные критерии — это измерения для определения успеха и неудачи альтернатив. Этот шаг содержит вторичный и окончательный анализ, а также вторичные решения проблемы. Примерами этого являются пригодность сайта и анализ его чувствительности. После тщательного прохождения процесса определения проблемы, изучения всех возможных альтернатив для нее и сбора информации на этом этапе предлагается оценить информацию и возможные варианты, чтобы предвидеть последствия каждой возможной альтернативы, о которой идет речь. На этом этапе необязательные критерии для измерения успеха или неудачи принятого решения должны быть рассмотрены. Рациональная модель планирования опирается в основном на объективную оценку.
На основе критериев оценки и анализа, проведенного на предыдущих этапах, выбирается лучшее сгенерированное решение. Эти четыре шага составляют ядро модели Rational Decision Decision, основанной на процессах рациональных решений.
Этот этап включает в себя окончательную реализацию сайта и предварительный мониторинг результатов. Этот шаг является частью процесса строительства/ ремонта и содержит вторичный и окончательный мониторинг результатов. Он происходит в течение длительного периода времени и позволяет изменить будущие решения и действия, предпринятые на основе вышеуказанной оценки результатов. Это и является рациональным решением.
Некоторые критерии, такие как экономическая выгода, будет легче измерить или определить, в то время как другие, такие как качество окружающей среды, будет сложнее выразить количественно. Однако в конечном итоге набор критериев принятия решений должен включать в себя все цели политики, а переоценка более легко определяемых или измеримых критериев окажет нежелательное влияние на смещение анализа к подмножеству целей политики.
Процесс определения достаточно всеобъемлющего набора критериев принятия решений также подвержен перекосам из-за давления, возникающего на политическом взаимодействии. Например, лица, принимающие решения, могут иметь тенденцию придавать больший вес политическим воздействиям, которые являются концентрированными, ощутимыми, определенными и немедленными, чем воздействиям, которые являются диффузными, нематериальными, неопределенными и задержанными. Например, при использовании системы ограничения выбросов и торговли квотами на выбросы углерода чистые финансовые затраты в первые пять лет реализации политики гораздо легче воздействуют на концептуализацию, чем более размытое и неопределенное влияние улучшенной позиции страны по влиянию на глобальные переговоры по действиям по изменению климата.
Моделирование
Отображение воздействия альтернатив политики может быть выполнено с использованием матрицы анализа политики (PAM). PAM предоставляет сводку воздействий политики для различных альтернатив, и анализ матрицы может выявить компромиссы, связанные с этим. Рациональное управленческое решение — это очень важно.
После того как альтернативы политики были оценены, следующий шаг должен содержать решение, какая альтернатива политики должна быть реализована. В одном крайнем случае сравнение альтернатив политики может быть относительно простым, если все ее цели можно измерить с использованием одного показателя и с одинаковым весом. В этом случае метод принятия решения — это анализ затрат на пособие (BCA).
С другой стороны, многочисленные цели потребуют выражения политических воздействий с использованием различных метрик, которые трудно сопоставимы. В таких случаях политический аналитик может опираться на концепцию полезности для объединения различных целей в единую оценку. В соответствии с концепцией полезности каждому воздействию присваивается такой вес, что одна единица каждого взвешенного воздействия считается одинаково ценной (или желательной) с точки зрения коллективного благосостояния.
Ваймер и Вайнинг также предполагают, что правило «ходи, не ходи» может быть полезным методом для выбора среди альтернатив политики. В соответствии с этим режимом принятия решений некоторым или всем политическим воздействиям могут быть назначены пороговые значения, которые используются для устранения по крайней мере некоторых из политических альтернатив. Таким образом, любая альтернатива политики, которая не соответствует этому пороговому значению, может быть исключена из рассмотрения. Если только одна альтернатива политики удовлетворяет всем порогам воздействия, то именно она считается «ходом» для каждого воздействия. В противном случае может случиться так, что будут исключены все, кроме нескольких политических альтернатив, и те, которые остаются, должны быть более тщательно изучены с точки зрения их компромиссов, чтобы можно было принять решение.
Демонстрация
Чтобы продемонстрировать процесс рационального анализа, как описано выше, давайте рассмотрим программный документ «Стимулирование использования биотоплива в Европейском союзе: последствия для политики в области изменения климата» Лизы Райан, где в Европейском союзе была предложена замена ископаемого топлива биотопливом в период 2005-2010 годов в рамках стратегии по снижению выбросов парниковых газов от автомобильного транспорта, повышению безопасности энергоснабжения и поддержке развития сельских общин. Метод принятия рационального решения — очень передовой и используется практически во всех сферах жизни.
Тем не менее существует много предположений, требований, без которых рациональная модель принятия решений не удается. Поэтому все они должны быть рассмотрены. Модель предполагает, что мы или имеем, или должны, или можем получить адекватную информацию с точки зрения качества, количества и точности. Это относится как к основной ситуации, так и к альтернативным техническим. Далее предполагается, что вы или имеете, или должны, или можете получить существенные знания о причинно-следственных связях, имеющих отношение к оценке альтернатив. Другими словами, это предполагает, что вы хорошо знаете все альтернативы и последствия выбранных вариантов. Далее предполагается, что вы можете ранжировать их и выбрать лучший из них. Решение рационально-дробных чисел — популярный метод в математике.

В то время как модель рационального планирования была инновационной по своей концепции, сами концепции сегодня являются спорными и сомнительными процессами. Модель рационального планирования вышла из массового использования в последнее десятилетие. Люси Сучман утверждает, что вместо того, чтобы осмысливать человеческих агентов как рациональных планировщиков, их можно лучше понимать как вовлеченных в действия на месте. Идя дальше, Ги Бенвенисте утверждал, что рациональная модель не может быть реализована без учета политического контекста. Рациональное решение проблем — это важная и интересная задача.
Прочие модели
Рациональные модели принятия решений включают когнитивный процесс, где каждый шаг следует в логическом порядке по сравнению с предыдущим. Под когнитивным подразумевается, что оно основано на продумывании и взвешивании альтернатив, чтобы получить наилучший потенциальный результат.
Существуют различные типы рациональных моделей, и количество используемых шагов и даже сами шаги будут отличаться в разных моделях.
Некоторые люди предполагают, что принятие решений эквивалентно решению проблем. Некоторые решения, однако, не ориентированы на проблемы.
Сравнение часто выполняется путем заполнения форм или диаграмм, которые имеют много имен. Матрица решений, матрица Пью, матрица выбора, форма рейтинга критериев и другие. Относительная важность придается каждому критерию, а варианты оцениваются по каждому критерию и наибольшим «выигрышам». Решение дробно-рациональных неравенств весьма популярно в математике.
Рациональная модель принятия решений предполагает, что есть один лучший результат. Из-за этого его иногда называют оптимизирующей моделью принятия решений. Поиск совершенства часто является фактором фактической задержки принятия решения.
Такая модель также предполагает, что можно рассмотреть каждый вариант, а также узнать будущие последствия каждого. Хотя многие хотели бы думать, что они знают, что произойдет, у Вселенной часто есть другие планы.
Это также ограничено познавательными способностями человека, принимающего решение. Насколько хороша их память? Насколько хороша их фантазия? Сами критерии, конечно, будут субъективными, и их будет сложно сравнивать. Эти модели требуют много времени и большого количества информации. И, конечно, рациональная модель принятия решений пытается свести на нет роль эмоций в процессе.
Говорят, что лица, принимающие решения, проявляют ограниченную рациональность, когда они рассматривают меньшее количество вариантов, чем фактически доступно, или когда они выбирают вариант, который не является лучшим в целом, но наилучшим в текущих условиях. Например, кто-то разливает кофе на рубашку в ресторане, идет в магазин по соседству и покупает плохо облегающую рубашку, чтобы немедленно переодеться. В этом отношении весьма эффективно решение рациональных неравенств.
Очевидно, было бы оптимальным купить подходящую рубашку. Но если человек спешит и не может носить мокрую, испачканную кофе одежду, тогда уместно покупать и плохо подходящую веь. Это называется удовлетворительным способом рационального решения.
Когда вы думаете об этом, большинство наших решений таковы отчасти потому, что мы экономим время, не рассматривая каждую доступную нам возможность. Мы выбираем только самые полезные. Рациональные примеры с решениями также популярны в школах, ибо польза от них весьма велика.
История
Эта модель изначально была создана Врумом и Йеттоном в 1973 году, а затем модифицирована Врумом и Яго. По сути, существует пять ситуаций для принятия решений, от одного лица, принимающего решение, до лица с различными объемами информации по сравнению с остальной частью группы и до всей группы.
Модель принятия решений Vroom-Jago содержит серию из семи вопросов с ответами «да» либо «нет», в которых выявляются важные критерии и указывается, какой из пяти процессов принятия решений является наиболее подходящим.
Заключение
Принятие решений является очень важным процессом во всех смыслах этого слова. Без него невозможно существование современной политической и социальной реакции, потому что волевой стержень человека стремится к своему тотальному выражению через матрицу совершения выбора. В информатике, математике и смешанных сферах, однако, этим словосочетанием названо несколько иное явление, и именно этому значению посвящена статья. Это очень важно понимать и осознавать всем, кто ее прочитал, особенно людям, которые собираются часто совепшать рациональные решения, методы и особенности которых весьма разнообразны. Это можно заметить и по изложенной в статье информации.
Очень важно также понимать, насколько важны решения. В современных компаниях огромная ответственность лежит именно на десижн-мейкерах, определяющих значительную часть деятельности медиахолдингов. Потому эта тема так интересна всем молодым и амбициозным специалистам.
Примеры с рациональными числами, решение которых играет большую роль в физике и естественных науках, были составлены как раз благодаря изучению темы, которой посвящена эта статья.
Лекции по торговым вычислениям: «Рациональные способы вычисления»
Рациональные приемы вычислений в схемах.
Название приема: Умножение на 5, 50, 500 и т.д..
Описание приема:
Способ. Число делим на 2, затем умножаем на 10.
Способ. Число умножаем на 10, затем делим на 2.
Обоснование приема: а 5=(а:2)
5=(а:2) (5
(5 2)=а:2
2)=а:2 10
10
а 5=(а
5=(а 5
5 2):2=а
2):2=а 10:2
10:2
Схема:
Примеры: 25,8 5=25,8
5=25,8 10:2=258:2=129
10:2=258:2=129
654,56 50= 654,56
50= 654,56 100:2=65456:2=32728
100:2=65456:2=32728
Методические рекомендации
Данный прием вводится на частном примере при знакомстве с темой «Признаки делимости». Перед объяснением данного приема необходимо с учащимися повторить умножение чисел на 10, 100, 1000 и признак делимости на 2. На следующем этапе формулируем правило на котором основывается данный прием и знакомим с алгоритмом вычисления, сопровождая записью на доске. При закреплении данного приема учащиеся в начале решают примеры с подробным объяснением с помощью учителя, затем самостоятельно.
Название приема Деление числа на 5, 50, 500 и т.д.
Описание приема:
Делим на 10, 100, 1000 и т.д., затем умножаем на 2.
Делимое умножается на 2 и полученное произведение делится на 10, 100, 1000 и т.д.
Обоснование приема: а:5=(а:(5 2))
2))  2=а:10·2
2=а:10·2
Схема: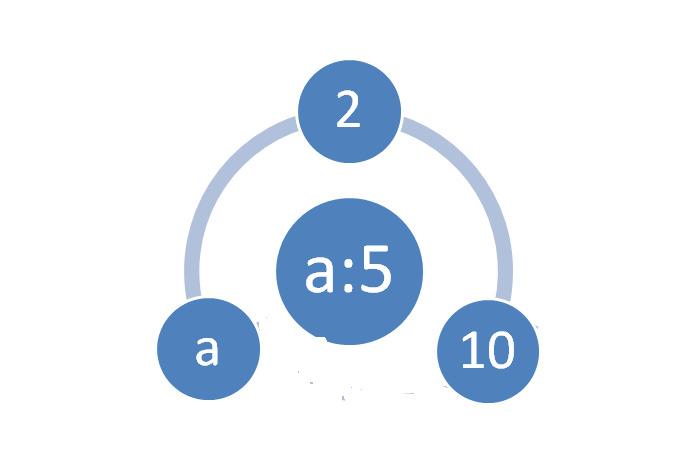
1) 9740: 5 = (9740: 10) 2 = 974  2= 1948;
2= 1948;
2) 198500: 50 = (198500: 100)  2 = 3970;
2 = 3970;
3) 4,7: 500 = (4,7  2): (500
2): (500 2) = 9,4: 1000 = 0,0094
2) = 9,4: 1000 = 0,0094
Методические рекомендации:
Перед тем, как учащихся познакомить с данным приемом необходимо с ними повторить признаки делимости на 10,100, 1000 . Затем познакомить их с правилом на котором основан прием, затем подробно разобрать алгоритм решения примеров данного типа. Закрепление этого приема происходит в начале с подробным объяснением, затем без него.
Название приема: Умножение на 25, 250, 2500 и т.д.
Описание приема:
1способ. Число делим на 100, затем умножаем на 4.
2 способ. Делимое умножаем на 4, затем делим на 100.
Обоснование приема:
а  25=(а:4)
25=(а:4)  (25
(25 4)=а:4
4)=а:4 100
100
Схема:
543 25=(540:4)
25=(540:4)  100+3
100+3 25=135
25=135 100+3
100+3 25=13575
25=13575
96 250=(96:4)
250=(96:4)  (250
(250 4)=24
4)=24 1000=24000
1000=24000
75 2500=(75
2500=(75 10000):4=187500 .
10000):4=187500 .
Методические рекомендации:
Перед тем, как ввести данный прием учащиеся должны знать, что 100 это произведение чисел 25 и 4. Далее знакомим с правилом, объясняя подробно алгоритм вычисления и закрепляем на примерах.
Название приема: деление на 25, 250
Описание приема:
1способ
1.разделить его на 100, 1000 и т.д. и
2. полученное частное умножить на 4.
2 способ
1. сначала делимое умножить на 4,
2. разделить на100
Обоснование приема: а:25=(а·4):(25·4)=а·4:100
Схема:
14, 4: 25 = (14,4: 100)·4 = 0,144·4= 0,576, или
14,4: 25 = (14,4·4): (25·4) = 57,6: 100 = 0,576
67.32:25=(64.32:100)·4=1684
Методические рекомендации:
На первом этапе знакомства с делением числа на 25 необходимо вспомнить с учащимися, что 25 составляет четвертую часть от ста. Далее знакомим с правилом, показывая как можно вычислить, разбирая каждый способ подробно на доске. Для закрепления используем карточки – подсказки.
Название приема: Умножение на 125, 1250 и т.д.
Описание приема:
1 способ
Данное число умножают на 1000, 10000 и т.д.,затем полученное произведение делят на 8. Или:
2 способ
данное число делят на 8 затем полученное частное умножают на 1000, 10000 и т.д.
Обоснование приема:
а·125=а·(100+25)=а:8·(125·8)=а:8·1000
Схема:
72 125= (72: 8)
125= (72: 8)  (125
(125 8) = 9
8) = 9 1000 = 9000, или
1000 = 9000, или
72 125= 72
125= 72 (100 + 25) = 72
(100 + 25) = 72 100 + 72: 4
100 + 72: 4 100 = 7200 + 1800 = 9000
100 = 7200 + 1800 = 9000
13,25·125=13,28·1000:8=1660
Методические рекомендации:
При введении данного приема нужно вспомнить с учащимися, что 125 составляет восьмую часть от 1000.Далее показываю алгоритм вычисления на конкретном примере с подробным объяснением. Закрепление можно провести в виде игры «Попади в цель».
Название приема: Деление числа на 125
Описание приема
1 способ.
При делении числа на 125, 1250 и т.д. достаточно разделить его на 1000, 10000 и т.д., а затем полученное частное умножить на 8.
2 способ
сначала делимое умножить на 8, а потом полученное произведение разделить на 1000, 10000 и т.д.
Обоснование приема:
а: 125=а·8: (125·8)=а·8:1000
Схема:
1) 35000: 125 = (35000: 1000)  8 = 35
8 = 35 8 = 280;
8 = 280;
2) 32250: 125 = (32250 8): (125
8): (125 8) = 258000: 1000 = 258.
8) = 258000: 1000 = 258.
Методические рекомендации:
Данный прием вводится аналогично предыдущему.
Название приема: умножение на 15.
Описание приема: число умножаем на 10, далее берем его половину, затем все складываем.
Обоснование приема:
а·15=а·(10+5)=а·(10+2·5:2)= а·10+(а·10:2)
Схема:
1850·15=1850·10+(1850·10):2=27750
2,48·15=2.48·10+1,24=3,72
Методические рекомендации:
В начале нужно обратить внимание учащихся , что 15 состоит из 1 десятка и 5 единиц, а 5 – это половина десятка. Далее знакомим с правилом и на конкретном примере показываем способ вычисления. Закрепление проводится с подробным объяснением.
Название приема: Умножение на 37
Описание приема:
1способ
Если данное число кратно 3, его делят на 3 и умножают на 111
2 способ
Если же данное число не кратно 3, то из произведения вычитают 37 или к произведению прибавляют 37
Обоснование приема: а:37= (а:3)·37·3=а:3·111
Схема:
24 37=(24:3)
37=(24:3)  (37
(37 3)=8
3)=8 111=999.
111=999.
18·37=18:3·111=666
23 37=(24-1)
37=(24-1)  37=(24:3)
37=(24:3)  (37
(37 3)-37=888=37=851
3)-37=888=37=851
28 37=(27-1)
37=(27-1)  37=27
37=27 37+37=999+37=1036
37+37=999+37=1036
Методические рекомендации:
Прежде чем ввести данный прием нужно с учащимися хорошо отработать таблицу умножения на 3 и признаки делимости на 3. После чего познакомить с алгоритмом вычисления, сопровождая записью на доске. Закрепляем его в начале с подробным объяснением, после чего без него.
Название приема: Умножение на 9, 99, 999 и.т.д.
Описание приема:
Умножаем на 10, затем из полученного результата вычитаем само число.
Обоснование приема:
а·9=а·(10-1)=а·10-а·1=а·10-а
Схема:
576·9=576·10-567=5184
3546·99=3546·100-3546=351054
Методические рекомендации:
Повторить с учащимися состав числа 10, обращая внимание на то, что 10 это сумма чисел 9 и 1, необходимо вспомнить распределительное свойство умножения относительно вычитания. Только после этого учащихся знакомим с правилом вычисления, сопровождая записями на доске. После чего закрепляем данный алгоритм вычисления.
Название приема: Умножение на 11.
Описание приема:
Необходимо «раздвинуть» цифры числа, умножаемого на 11, затем в образовавшийся промежуток вписать сумму этих цифр, если эта сумма больше 9, то, как при обычном сложении, следует единицу перенести в старший разряд.
Пример:
34 * 11 = 374, так как 3 + 4 = 7, семерку помещаем между тройкой и четверкой
68 * 11 = 748, так как 6 + 8 = 14, четверку помещаем между семеркой (шестерка плюс перенесенная единица) и восьмеркой
Обоснование::
10a+b – любое число, где a — число десятков, b — число единиц. :
(10a+b)·11 = 10a·11 + b·11 = 110a + 11b = 100a + 10a + 10b + b = 100a + 10·(a+b) + b,
где мы имеем a сотен, a+b десятков и b единиц. т.е. результат содержит a·(a+1)сотен, два десятка и пять единиц.
Схема:
42172·11
Составляем произведение: 2 единицы, 7+2=9 десятки, 7+1=8 сотни, 1+2=3тысячи, 2+4=6 десятки тысяч, 4 сотни тысяч.
43625*11=463892.
18·11=1(8+1)8=198
75·11=7(7+5)5=7(12)5=825
4315·11=4315·10+4315=46465
Методические рекомендации.
На конкретных примерах рассматриваем с учащимися различные приемы умножения числа на 11. В нале знакомятся с правилами вычисленця , а затем закрепляем данный прием с помощью карточек- помощниц.
Название приема: Умножение двузначного числа на 101.
Описание приема: Припишите число к самому себе
Обоснование приема:
(10a+b)*101 = 1010a + 101b = 1000a + 100b + 10a + b
Примеры:
43·101=4343 89·1001=898989
27·101=2727 65·1001=656565
Методические рекомендации:
Данный прием очень простой, Поэтому необходимо обратить внимание учащихся на количестве нулей в множителе, Достаточно сказать им, что нужно приписать столько раз число сколько нулей в множителе.
Авторская программа прикладного курса. Рациональный способ решения текстовых задач.
ММ «Лесной орта мекткбі»
Сандықтау ауданы
Ақмола обласы
ГУ «Лесная средняя школа»
Сандыктауского района
Акмолинской области
Программа прикладного курса
«Рациональный способ решения текстовых задач»
Автор: Кононова Наталья Геннадьевна – учитель математики.
Утверждена решением педагогического совета: 5 апреля 2014 г.
Пояснительная записка.
Всякая хорошо решенная задача
доставляет умственное наслаждение.
Г. Гессе.
Целью данной авторской программы, как одного из направлений модернизации математического образования, является обеспечение углубленного изучения предмета и подготовка учащихся к продолжению образования. Решение текстовых задач у многих учащихся вызывает затруднения. Универсальных методов решения текстовых задач не существует, но, решая такие задачи, можно придерживаться приведенной ниже схемы:
Выбрать неизвестные.
В большинстве случаев удобно за неизвестное взять ту величину, которую требуется определить в задаче. Такой вариант следует рассматривать в первую очередь, но это правило не является жестким, иногда проще составить уравнения, в которые входят другие величины, и лишь после их определения найти окончательный ответ. Важным моментом является число неизвестных; чем больше неизвестных, тем легче составлять уравнения (или неравенства), но при этом усложняется само решение; не надо вводить новые неизвестные, если какая то величина элементарно выражается через уже введенные.
2. Составить уравнения (возможно неравенства).
В процессе составления системы уравнений важно использовать все условия задачи. Количество уравнений должно совпадать с количеством неизвестных, за исключением случая, когда требуется найти не сами величины, а лишь некоторое соотношение между ними.
3. Найти нужное неизвестное или нужную комбинацию неизвестных.
Если приходится отбрасывать некоторые корни, полученные в ходе решения, то это необходимо делать исходя из условий задачи, а не из соображений здравого смысла.
Текстовые задачи удобно классифицировать по следующим группам:
задачи на движение;
задачи на работу и производительность труда;
задачи на концентрацию и процентное содержание;
задачи на зависимость между компонентами арифметических действий;
задачи на проценты.
В школьном курсе математики решение текстовых задач считается одним из сложных для восприятия и усвоения учащимися разделов. С моей точки зрения это связано с не разработанностью аналитического аппарата, который бы позволял рассматривать любую текстовую задачу как систему, в независимости от того, является ли она задачей на движение, на работу, на смеси или сплавы, на проценты и т. д. поэтому я предлагаю данную программу внедрять в 7 – 8 классах, так как именно в этих классах учащиеся начинают подробно и более глубоко заниматься решением текстовых задач.
Разработанная программа направлена на решение следующих задач:
повышение уровня математического и логического мышления учащихся;
формирование у учащихся устойчивого интереса к предмету;
выявление и развитие их математических способностей
подготовка к ЕНТ и к обучению в вузе.
Учебно – тематический план (1 ч в неделю, всего 34 ч)
№ п/п
Название
разделов и тем
Количество часов
Форма проведения
Дата проведения
всего
теории
практики
1
Задачи на движение.
8
1,5
6,5
1.1
Движение судна в стоячей воде.
0,5
1
лекция
практикум
1.2
Движение судна по течению реки.
1,5
практикум
1.3
Движение судна против течения реки.
1,5
практикум
1.4
Движение автотранспорта.
0,5
1,5
лекция
практикум
1.5
Движение по окружности.
0,5
1
лекция
практикум
2
Задачи на работу и производительность труда.
7
1,5
5,5
2.1
Простые задачи на работу и производительность.
0,5
2
лекция
практикум
2.2
Задачи на совместную работу.
0,5
1,5
лекция
практикум
2.3
Задачи на бассейн, который наполняется одновременно разными трубами.
0,5
2
лекция
практикум
3
Задачи на концентрацию и процентное содержание.
5
1,5
3,5
3.1
Задачи на смеси.
0,5
1
лекция
практикум
3.2
Задачи на сплавы.
0,5
1
лекция
практикум
3.3
Задачи на концентрацию и процентное содержание.
0,5
1,5
лекция
практикум
4
Задачи на зависимость между компонентами арифметических действий.
7
1,5
5,5
4.1
Задачи, в которых используется формула числа.
0,5
1,5
лекция
практикум
4.2
Задачи, в которых слагаемые пропорциональны некоторым числам (или дано их отношение).
0,5
2
лекция
практикум
4.3
Задачи, где неизвестные являются членами пропорции.
0,5
2
лекция
практикум
5
Задачи на проценты.
7
1,5
5,5
5.1
Составление пропорции.
0,5
2
лекция
практикум
5.2
Сложный процентный рост.
0,5
1,5
лекция
практикум
5.3
Решение задач на проценты алгебраическим методом.
0,5
2
лекция
практикум
Итого.
34
7,5
26,5
Указания к решению текстовых задач
Набор неизвестных должен быть достаточным для перевода условий задачи на язык математических соотношений. Как правило, за неизвестные следует принимать искомые величины.
Выбрав неизвестные, в процессе перевода условий задачи в уравнения или неравенства необходимо использовать все данные и условия задачи.
При составлении уравнений или неравенств необходимо исходить из требования о решении задачи в общем виде.
В составленных уравнениях надо проверить размерность членов уравнений
В процессе решения задачи, надо избегать результатов, противоречащих физическому смыслу.
Тема авторской работы является одной из актуальных в современной методике преподавания математики, так как в большинстве случаев решение текстовых задач вызывает трудности у учащихся. Умение решать задачи является одним из основных показателей уровня математического развития, глубины усвоения учебного материала. С начала и до конца обучения в школе математическая задача неизменно помогает ученику вырабатывать правильные математические понятия, глубже выяснять различные стороны взаимосвязей в окружающей его жизни, дает возможность применять изучаемые теоретические положения. Текстовые задачи – традиционно трудный для значительной части школьников материал. Однако в школьном курсе математики ему придается большое значение, так как такие задачи способствуют развитию логического мышления, речи и других качеств продуктивной деятельности обучающихся.
Рациональные способы решения квадратных уравнений

Курс повышения квалификации
Курс повышения квалификации

Курс профессиональной переподготовки
Учитель математики и информатики
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию:
Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс:
Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник:
Все учебники
Выберите тему:
Все темы
также Вы можете выбрать тип материала:

Общая информация
Номер материала:
512329
Похожие материалы
Оставьте свой комментарий
Третий путь — RationalWiki
| «» Я рад видеть, что дебаты ведутся на нашей стороне поля, но может возникнуть огромная обратная реакция, если левые не выполнят своих обязательств. В конечном счете, в условиях демократии бедные полагаются на социальное суждение среднего класса. |
| — Билл Клинтон в разговоре с Тони Блэром, 1997. [1] |
Третий путь (или Экономический рационализм , если вы австралиец) — это школа политической мысли, которая пытается примирить капитализм и социализм: объединяя рыночные экономические порядки с политикой перераспределения.По сути, это означает признание того, что ряд богатых людей попали в этот путь отчасти случайно, и что более бедные люди могут оказаться бедными из-за обстоятельств, не зависящих от них.
Поскольку они не попадают прямо ни в левую, ни в правую сторону, они воспринимаются как нечто отличное от обоих, но, по-видимому, недостаточно отчетливо, чтобы заслужить более творческое название.
Политика «третьего пути» настолько близка к действительному центризму, насколько это возможно, хотя ее отвергают как экономику правого толка. [2] Многие отмечали сходство между демократами третьего пути и Республиканской партией до 1964 года.
Адвокаты [править]
Наиболее известные сторонники «Третьего пути» вышли из реформистских партий начала и конца 1990-х, таких как «Новые демократы» Билла Клинтона, «Новые лейбористы» Тони Блэра или немецкая СДПГ под руководством Герхарда Шредера.
Другие включают Боба Хоука и Пола Китинга из Австралийской лейбористской партии (который изобрел доктрину третьего пути) в 1983-96 годах, Роджера Дугласа из Новой Зеландии с 1984 по 1988 год, Фернандо Энрике Кардозу из Бразилии, Вима Кока из Нидерландов и Хосе Сократеса из Португалии. ,
Плюсы и минусы [править]
| «» «Моя партия отсутствовала на Даунинг-стрит, 10 в течение 18 лет. Когда вы выигрываете выборы, вы выходите на Даунинг-стрит на следующий день, и предшественник выходит через черный ход, как только входит новый премьер-министр. помню, когда я вошел в свой первый день. Персонал аплодировал бывшему премьер-министру. Когда я вошел. Персонал плакал. Я чувствовал себя виноватым за все это. Я вошел в кабинет. Главный государственный служащий — очень великий человек — сказал мне и очень по-британски.»Отлично сработано. Что теперь?» Это великий вопрос управления. Вы можете быть отличным коммуникатором, который поможет вам получить работу, но, придя к власти, вы станете генеральным директором и вам нужно будет вести бизнес. |
| — Тони Блэр в 2015 году [3] |
Существует много разных моделей, но большинство склонялось к социал-демократическим подходам к управлению, чаще всего:
- Поддержание социальных программ европейского образца
- Централизация управления
- Ослепление финансовых институтов
- Дерегулирование и приватизация
- Ястребиная внешняя политика
- Авторитарный, когда ему не все равно (разрушение профсоюзов, борьба с терроризмом), социально либеральный, когда это не так (равные права, приговоры за наркотики)
- Наивно технократический
- Безжалостно эффективно побеждать на выборах
Короче говоря, все было о равенстве возможностей, а не о старой идее равенства результатов.Такие партии годами занимали политический центр, повышая свои электоральные шансы. В большинстве англоязычных стран центр с тех пор стал очень переполненным, поскольку каждая крупная партия копировала свои действия. Это уменьшило общее расстояние между левыми и правыми на какое-то время, и поэтому термин в основном вышел из моды (или был заменен на «неолиберализм»). Однако нынешний всплеск популизма как среди левых, так и среди правых в сочетании с усилением поляризации в целом сильно ослабил его.
Это также обеспечило приемлемое прикрытие для неограниченного капитализма на всех уровнях. Либертарианское движение отказалось от этого притворства.
Другое использование [править]
- «Третий путь» иногда рассматривается и / или неправильно понимается как эвфемизм для защиты фашизма, хотя они, вероятно, думают о третьем позиционизме.
- Третий путь — британский журнал «христианских комментариев о культуре» для вменяемых англиканцев. [1]
См. Также [править]
Ссылки [править]
,
Область и диапазон рациональных функций
Область рациональной функции
Пусть y = f (x) — функция.
Домен — это все действительные значения x, для которых определено y.
Если существует какое-либо значение x, для которого y не определено, мы должны исключить это конкретное значение из набора домена.
Пример:
Рассмотрим приведенную ниже рациональную функцию.
y = 1 / (x — 2)
В приведенной выше рациональной функции приравняем знаменатель x — 2 к нулю.
x — 2 = 0
x = 2
В функции
y = (x 2 — x — 2) / (x — 2),
если x = 2, то знаменатель становится равным нулю и значение «y» становится неопределенным.
Итак, «y» определено для всех действительных значений «x», кроме x = 2.
Следовательно, домен равен
R — {2}
Диапазон рациональной функции
Пусть y = f (x) — функция.
Диапазон — это не что иное, как все реальные значения y для данного домена (реальные значения x).
Пример:
Рассмотрим приведенную ниже рациональную функцию.
y = 1 / (x — 2)
Чтобы найти диапазон рациональной функции выше, сначала мы должны найти обратную y.
Чтобы найти обратное значение y, выполните следующие действия.
Шаг 1:
y = 1 / (x — 2) был определен y через x.
Эта же функция должна быть переопределена x через y.
Шаг 2:
y = 1 / (x — 2)
Умножьте каждую сторону на (x — 2).
(x — 2) y = 1
xy — 2y = 1
Добавьте 2y с каждой стороны.
xy = 2y + 1
Разделите каждую сторону на y.
x = (2y + 1) / y
Теперь функция была определена посредством x через y.
Шаг 3:
В x = (2y + 1) / y мы должны заменить x на y -1 и y на x.
Затем
y -1 = (2x + 1) / x
Шаг 4:
Теперь найдите домен y -1 .
В обратной функции y -1 , если мы заменим 0 на x, знаменатель станет нулевым, а значение y -1 станет неопределенным.
y -1 определяется для всех действительных значений x, кроме нуля.
Итак, домен y -1 равен
R — {0}
И мы уже знаем тот факт, что
Range (y) = Domain (y -1 )
Следовательно, диапазон из y составляет
R — {0}
Другой способ найти диапазон рациональных функций
Для
некоторые рациональные функции, обратную функцию найти немного сложно.В этом случае мы должны нарисовать график рациональной функции, используя
вертикальная асимптота, горизонтальная асимптота и таблица значений, как указано
ниже.
Таким образом, мы легко можем получить набор рациональных функций.
Давайте посмотрим, как найти диапазон приведенной ниже рациональной функции.
y = 1 / (x — 2)
Вертикальная асимптота:
Чтобы найти вертикальную асимптоту, мы должны сделать знаменатель (x — 2) равным нулю.
Когда мы это сделаем,
x — 2 = 0
x = 2
Итак, вертикальная асимптота будет
x = 2
Горизонтальная асимптота:
дюймов
рациональная функция y = 1 / (x — 2), старший показатель числителя
меньше старшего показателя знаменателя.
Итак, существует горизонтальная асимптота.
Уравнение горизонтальной асимтоты:
y = 0
Таблица значений:
В данной рациональной функции y = 1 / (x-2), теперь мы должны заменить некоторые случайные значения на x и найти соответствующие значения y.
Мы уже знаем, что вертикальная асимптота равна
x = 2
Теперь,
мы должны взять некоторые случайные значения для x в следующие интервалы.
x <2, x> 2, но не x = 2
(поскольку x = 2 — вертикальная асимптота)
График y = 1 / (x — 2) ‘
Когда мы смотрим на приведенный выше график, становится ясно следующее.
То есть график (красным цветом) рациональной функции
y = 1 / (x — 2)
появляется при каждом действительном значении y, кроме y = 0.
Из графика ясно видно, что диапазон y составляет
R — {0}
Кроме того, что описано в этом разделе, если вам нужны другие математические данные, воспользуйтесь нашим пользовательским поиском Google здесь.
Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.
ЗАДАЧИ СО СЛОВАМИ
Задачи со словами HCF и LCM
Задачи со словами на простых уравнениях
Задачи со словами на линейных уравнениях
Задачи со словами на квадратных уравнениях
Алгебраные задачи со словами 9000
Проблемы со словами в поездах
Проблемы со словами по площади и периметру
Проблемы со словами по прямой и обратной вариации
Проблемы со словами по цене за единицу
Проблемы со словами по цене за единицу
Word задачи по сравнению ставок
Преобразование общепринятых единиц в текстовые задачи
Преобразование в метрические единицы в текстовых задачах
Словарные задачи по простому проценту
Словарные задачи по сложным процентам
Словарные задачи по типам ngles
Проблемы с дополнительными и дополнительными углами в словах
Проблемы со словами с двойными фактами
Проблемы со словами в тригонометрии
Проблемы со словами в процентах
Проблемы со словами о прибылях и убытках
Разметка и разметка Задачи
Задачи с десятичными словами
Задачи со словами о дробях
Задачи со словами о смешанных фракциях
Одношаговые задачи с уравнениями со словами
Проблемы со словами о линейных неравенствах
Соотношение и пропорции Задачи со словами
Проблемы со временем и рабочими словами
Задачи со словами на множествах и диаграммах Венна
Задачи со словами на возрастах
Проблемы со словами в теореме Пифагора
Процент числового слова pr проблемы
Проблемы со словами при постоянной скорости
Проблемы со словами при средней скорости
Проблемы со словами на сумме углов треугольника 180 градусов
ДРУГИЕ ТЕМЫ
Сокращения прибылей и убытков
Сокращение в процентах
Сокращение в таблице времен
Сокращение времени, скорости и расстояния
Сокращение соотношения и пропорции
Домен и диапазон рациональных функций
Область и диапазон рациональных функций функции с отверстиями
График рациональных функций
График рациональных функций с отверстиями
Преобразование повторяющихся десятичных дробей в дроби
Десятичное представление рациональных чисел
Поиск квадратного корня с помощью long di видение
L.Метод CM для решения временных и рабочих задач
Преобразование задач со словами в алгебраические выражения
Остаток, когда 2 степени 256 делится на 17
Остаток при делении 17 степени 23 на 16
Сумма всех трехзначных чисел, делящихся на 6
Сумма всех трехзначных чисел, делимых на 7
Сумма всех трехзначных чисел, делящихся на 8
Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4
Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами
Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3
Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6
,
