Степень свободы что такое: Степени свободы — это… Что такое Степени свободы?
Степени свободы — это… Что такое Степени свободы?
Сте́пени свобо́ды — характеристики движения механической системы. Число степеней свободы определяет минимальное количество независимых переменных (обобщённых координат), необходимых для полного описания движения механической системы. Также число степеней свободы равно полному числу независимых уравнений, полностью описывающих динамику системы.
Состояние физической системы
Подавляющее большинство физических систем может находиться не в одном, а во многих состояниях, описываемых как непрерывными (например, координаты тела), так и дискретными (например, квантовые числа электрона в атоме) переменными. Независимые «направления», переменные, характеризующие состояния системы, называются степенями свободы.
При этом важно отметить, что число степеней свободы равно минимальному количеству таких переменных, необходимому для полного описания состояния системы. Например, положение математического маятника можно характеризовать как углом его поворота вокруг оси, так и двумя координатами положения материальной точки относительно оси. Однако у такого маятника всего лишь одна степень свободы, а не две (как может показаться во втором случае), поскольку одного только угла поворота достаточно для описания положения этой системы в любой момент времени.
Примеры
- Простейшая механическая система — материальная точка в трёхмерном пространстве — обладает тремя степенями свободы, так как её состояние полностью описывается тремя пространственными координатами.
- Абсолютно твёрдое тело обладает шестью степенями свободы, так как для полного описания положения такого тела достаточно задать три координаты центра масс и три угла, описывающих ориентацию тела (эти величины известны в быту как «наклон, подъём, поворот», в авиации их называют «крен, тангаж, рыскание»).
- Реальные тела обладают огромным числом степеней свободы (порядка числа частиц, из которых состоит тело). Однако в большинстве ситуаций оказывается, что наиболее важны лишь несколько «коллективных» степеней свободы, характеризующих движение центра масс тела, его вращение, его деформацию, его макроскопические колебания. Остальные же — микроскопические — степени свободы не заметны по отдельности, а воспринимаются сразу все вместе, как, например, температура и давление.
Обобщённые координаты
Понятие степени свободы связано с таким понятием, как размерность. В математике размерность — это количество независимых параметров, необходимых для описания состояния объекта, или, другими словами, для определения его положения в неком абстрактном пространстве.
При математическом описании состояния физической системы N степеням свободы отвечают N независимых переменных, называемых обобщёнными координатами.
В случае непрерывных степеней свободы соответствующие обобщённые координаты принимают непрерывный ряд значений. Однако можно рассматривать и дискретные степени свободы.
Примеры
- Для того, чтобы описать положение окружности на плоскости, достаточно трёх параметров: двух координат центра и радиуса, то есть пространство окружностей на плоскости трёхмерно. Окружность может быть перемещена в любую точку плоскости и её радиус может быть изменён, поэтому у неё три степени свободы.
- Для того, чтобы определить координаты объекта на географической карте, нужно указать широту и долготу. Соответствующее пространство поэтому называется двумерным. Объект может располагаться в любой точке, поэтому у каждого объекта на карте две степени свободы.
- Для задания положения самолёта нужно указать три координаты — дополнительно к широте и долготе нужно знать высоту, на которой он находится. Поэтому пространство, в котором находится самолёт, является трёхмерным. К этим трём координатам может быть добавлена четвёртая (время) для описания не только текущего положения самолёта, но и момента времени. Если добавить в модель ориентацию (крен, тангаж, рыскание) самолёта, то добавятся ещё три координаты и соответствующее абстрактное пространство модели станет семимерным.
См. также
О степенях свободы в статистике / Блог компании Stepik.org / Хабр
В одном из предыдущих постов мы обсудили, пожалуй, центральное понятие в анализе данных и проверке гипотез — p-уровень значимости. Если мы не применяем байесовский подход, то именно значение p-value мы используем для принятия решения о том, достаточно ли у нас оснований отклонить нулевую гипотезу нашего исследования, т.е. гордо заявить миру, что у нас были получены статистически значимые различия.
Однако в большинстве статистических тестов, используемых для проверки гипотез, (например, t-тест, регрессионный анализ, дисперсионный анализ) рядом с p-value всегда соседствует такой показатель как число степеней свободы, он же degrees of freedom или просто сокращенно df, о нем мы сегодня и поговорим.
Степени свободы, о чем речь?
По моему мнению, понятие степеней свободы в статистике примечательно тем, что оно одновременно является и одним из самым важных в прикладной статистике (нам необходимо знать df для расчета p-value в озвученных тестах), но вместе с тем и одним из самых сложных для понимания определений для студентов-нематематиков, изучающих статистику.
Давайте рассмотрим пример небольшого статистического исследования, чтобы понять, зачем нам нужен показатель df, и в чем же с ним такая проблема. Допустим, мы решили проверить гипотезу о том, что средний рост жителей Санкт-Петербурга равняется 170 сантиметрам. Для этих целей мы набрали выборку из 16 человек и получили следующие результаты: средний рост по выборке оказался равен 173 при стандартном отклонении равном 4. Для проверки нашей гипотезы можно использовать одновыборочный t-критерий Стьюдента, позволяющий оценить, как сильно выборочное среднее отклонилось от предполагаемого среднего в генеральной совокупности в единицах стандартной ошибки:
Проведем необходимые расчеты и получим, что значение t-критерия равняется 3, отлично, осталось рассчитать p-value и задача решена. Однако, ознакомившись с особенностями t-распределения мы выясним, что его форма различается в зависимости от числа степеней свобод, рассчитываемых по формуле n-1, где n — это число наблюдений в выборке:
Сама по себе формула для расчета df выглядит весьма дружелюбной, подставили число наблюдений, вычли единичку и ответ готов: осталось рассчитать значение p-value, которое в нашем случае равняется 0.004.
Но почему n минус один?
Когда я впервые в жизни на лекции по статистике столкнулся с этой процедурой, у меня как и у многих студентов возник законный вопрос: а почему мы вычитаем единицу? Почему мы не вычитаем двойку, например? И почему мы вообще должны что-то вычитать из числа наблюдений в нашей выборке?
В учебнике я прочитал следующее объяснение, которое еще не раз в дальнейшем встречал в качестве ответа на данный вопрос:
“Допустим мы знаем, чему равняется выборочное среднее, тогда нам необходимо знать только n-1 элементов выборки, чтобы безошибочно определить чему равняется оставшейся n элемент”. Звучит разумно, однако такое объяснение скорее описывает некоторый математический прием, чем объясняет зачем нам понадобилось его применять при расчете t-критерия. Следующее распространенное объяснение звучит следующим образом: число степеней свободы — это разность числа наблюдений и числа оцененных параметров. При использовании одновыборочного t-критерия мы оценили один параметр — среднее значение в генеральной совокупности, используя n элементов выборки, значит df = n-1.
Однако ни первое, ни второе объяснение так и не помогает понять, зачем же именно нам потребовалось вычитать число оцененных параметров из числа наблюдений?
Причем тут распределение Хи-квадрат Пирсона?
Давайте двинемся чуть дальше в поисках ответа. Сначала обратимся к определению t-распределения, очевидно, что все ответы скрыты именно в нем. Итак случайная величина:
имеет t-распределение с df = ν, при условии, что Z – случайная величина со стандартным нормальным распределением N(0; 1), V – случайная величина с распределением Хи-квадрат, с ν числом степеней свобод, случайные величины Z и V независимы. Это уже серьезный шаг вперед, оказывается, за число степеней свободы ответственна случайная величина с распределением Хи-квадрат в знаменателе нашей формулы.
Давайте тогда изучим определение распределения Хи-квадрат. Распределение Хи-квадрат с k степенями свободы — это распределение суммы квадратов k независимых стандартных нормальных случайных величин.
Кажется, мы уже совсем у цели, по крайней мере, теперь мы точно знаем, что такое число степеней свободы у распределения Хи-квадрат — это просто число независимых случайных величин с нормальным стандартным распределением, которые мы суммируем. Но все еще остается неясным, на каком этапе и зачем нам потребовалось вычитать единицу из этого значения?
Давайте рассмотрим небольшой пример, который наглядно иллюстрирует данную необходимость. Допустим, мы очень любим принимать важные жизненные решения, основываясь на результате подбрасывания монетки. Однако, последнее время, мы заподозрили нашу монетку в том, что у нее слишком часто выпадает орел. Чтобы попытаться отклонить гипотезу о том, что наша монетка на самом деле является честной, мы зафиксировали результаты 100 бросков и получили следующий результат: 60 раз выпал орел и только 40 раз выпала решка. Достаточно ли у нас оснований отклонить гипотезу о том, что монетка честная? В этом нам и поможет распределение Хи-квадрат Пирсона. Ведь если бы монетка была по настоящему честной, то ожидаемые, теоретические частоты выпадания орла и решки были бы одинаковыми, то есть 50 и 50. Легко рассчитать насколько сильно наблюдаемые частоты отклоняются от ожидаемых. Для этого рассчитаем расстояние Хи-квадрат Пирсона по, я думаю, знакомой большинству читателей формуле:
Где O — наблюдаемые, E — ожидаемые частоты.
Дело в том, что если верна нулевая гипотеза, то при многократном повторении нашего эксперимента распределение разности наблюдаемых и ожидаемых частот, деленная на корень из наблюдаемой частоты, может быть описано при помощи нормального стандартного распределения, а сумма квадратов k таких случайных нормальных величин это и будет по определению случайная величина, имеющая распределение Хи-квадрат.
Давайте проиллюстрируем этот тезис графически, допустим у нас есть две случайные, независимые величины, имеющих стандартное нормальное распределение. Тогда их совместное распределение будет выглядеть следующим образом:
При этом квадрат расстояния от нуля до каждой точки это и будет случайная величина, имеющая распределение Хи-квадрат с двумя степенями свободы. Вспомнив теорему Пифагора, легко убедиться, что данное расстояние и есть сумма квадратов значений обеих величин.
Пришло время вычесть единичку!
Ну а теперь кульминация нашего повествования. Возвращаемся к нашей формуле расчета расстояния Хи-квадрат для проверки честности монетки, подставим имеющиеся данные в формулу и получим, что расстояние Хи-квадрат Пирсона равняется 4. Однако для определения p-value нам необходимо знать число степеней свободы, ведь форма распределения Хи-квадрат зависит от этого параметра, соответственно и критическое значение также будет различаться в зависимости от этого параметра.
Теперь самое интересное. Предположим, что мы решили многократно повторять 100 бросков, и каждый раз мы записывали наблюдаемые частоты орлов и решек, рассчитывали требуемые показатели (разность наблюдаемых и ожидаемых частот, деленная на корень из ожидаемой частоты) и как и в предыдущем примере наносили их на график.
Легко заметить, что теперь все точки выстраиваются в одну линию. Все дело в том, что в случае с монеткой наши слагаемые не являются независимыми, зная общее число бросков и число решек, мы всегда можем точно определить выпавшее число орлов и наоборот, поэтому мы не можем сказать, что два наших слагаемых — это две независимые случайные величины. Также вы можете убедиться, что все точки действительно всегда будут лежать на одной прямой: если у нас выпало 30 орлов, значит решек было 70, если орлов 70, то решек 30 и т.д. Таким образом, несмотря на то, что в нашей формуле было два слагаемых, для расчета p-value мы будем использовать распределение Хи-квадрат с одной степенью свободы! Вот мы наконец-то добрались до момента, когда нам потребовалось вычесть единицу. Если бы мы проверяли гипотезу о том, что наша игральная кость с шестью гранями является честной, то мы бы использовали распределение Хи-квадрат с 5 степенями свободы. Ведь зная общее число бросков и наблюдаемые частоты выпадения любых пяти граней, мы всегда можем точно определить, чему равняется число выпадений шестой грани.
Все становится на свои места
Теперь, вооружившись этими знаниями, вернемся к t-тесту:
в знаменателе у нас находится стандартная ошибка, которая представляет собой выборочное стандартное отклонение, делённое на корень из объёма выборки. В расчет стандартного отклонения входит сумма квадратов отклонений наблюдаемых значений от их среднего значения — то есть сумма нескольких случайных положительных величин. А мы уже знаем, что сумма квадратов n случайных величин может быть описана при помощи распределения хи-квадрат. Однако, несмотря на то, что у нас n слагаемых, у данного распределения будет n-1 степень свободы, так как зная выборочное среднее и n-1 элементов выборки, мы всегда можем точно задать последний элемент (отсюда и берется это объяснение про среднее и n-1 элементов необходимых для однозначного определения n элемента)! Получается, в знаменателе t-статистики у нас спрятано распределение хи-квадрат c n-1 степенями свободы, которое используется для описания распределения выборочного стандартного отклонения! Таким образом, степени свободы в t-распределении на самом деле берутся из распределения хи-квадрат, которое спрятано в формуле t-статистики. Кстати, важно отметить, что все приведенные выше рассуждения справедливы, если исследуемый признак имеет нормальное распределение в генеральной совокупности (или размер выборки достаточно велик), и если бы у нас действительно стояла цель проверить гипотезу о среднем значении роста в популяции, возможно, было бы разумнее использовать непараметрический критерий.
Схожая логика расчета числа степеней свободы сохраняется и при работе с другими тестами, например, в регрессионном или дисперсионном анализе, все дело в случайных величинах с распределением Хи-квадрат, которые присутствуют в формулах для расчета соответствующих критериев.
Таким образом, чтобы правильно интерпретировать результаты статистических исследований и разбираться, откуда возникают все показатели, которые мы получаем при использовании даже такого простого критерия как одновыборочный t-тест, любому исследователю необходимо хорошо понимать, какие математические идеи лежат в основании статистических методов.
Онлайн курсы по статистике: объясняем сложные темы простым языком
Основываясь на опыте преподавания статистики в Институте биоинформатики , у нас возникла идея создать серию онлайн курсов, посвященных анализу данных, в которых в доступной для каждого форме будут объясняться наиболее важные темы, понимание которых необходимо для уверенного использования методов статистики при решении различного рода задача. В 2015 году мы запустили курс Основы статистики, на который к сегодняшнему дню записалось около 17 тысяч человек, три тысячи слушателей уже получили сертификат о его успешном завершении, а сам курс был награждён премией EdCrunch Awards и признан лучшим техническим курсом. В этом году на платформе stepik.org стартовало продолжение курса Основы статистики. Часть два, в котором мы продолжаем знакомство с основными методами статистики и разбираем наиболее сложные теоретические вопросы. Кстати, одной из главных тем курса является роль распределения Хи-квадрат Пирсона при проверке статистических гипотез. Так что если у вас все еще остались вопросы о том, зачем мы вычитаем единицу из общего числа наблюдений, ждем вас на курсе!
Стоит также отметить, что теоретические знания в области статистики будут определенно полезны не только тем, кто применяет статистику в академических целях, но и для тех, кто использует анализ данных в прикладных областях. Базовые знания в области статистики просто необходимы для освоения более сложных методов и подходов, которые используются в области машинного обучения и Data Mining. Таким образом, успешное прохождение наших курсов по введению в статистику — хороший старт в области анализа данных. Ну а если вы всерьез задумались о приобретении навыков работы с данными, думаем, вас может заинтересовать наша онлайн — программа по анализу данных, о которой мы подробнее писали здесь. Упомянутые курсы по статистике являются частью этой программы и позволят вам плавно погрузиться в мир статистики и машинного обучения. Однако пройти эти курсы без дедлайнов могут все желающие и вне контекста программы по анализу данных.
Степени свободы (физика) — это… Что такое Степени свободы (физика)?
Сте́пени свобо́ды — характеристики движения механической системы. Число степеней свободы определяет минимальное количество независимых переменных (обобщённых координат), необходимых для полного описания движения механической системы.
Также число степеней свободы равно полному числу независимых уравнений второго порядка (таких, как уравнения Лагранжа) или половине числа уравнений первого порядка (таких, как канонические уравнения Гамильтона), полностью описывающих[1] динамику системы.
Состояние физической системы
Подавляющее большинство физических систем может находиться не в одном, а во многих состояниях, описываемых как непрерывными (например, координаты тела), так и дискретными (например, квантовые числа электрона в атоме) переменными. Независимые «направления», переменные, характеризующие состояния системы, называются степенями свободы.
При этом важно отметить, что число степеней свободы равно минимальному количеству таких переменных, необходимому для полного описания состояния системы. Например, положение математического маятника можно характеризовать как углом его поворота вокруг оси, так и двумя координатами положения материальной точки относительно оси. Однако у такого маятника всего лишь одна степень свободы, а не две (как может показаться во втором случае), поскольку одного только угла поворота достаточно для описания положения этой системы в любой момент времени.
Примеры
- Простейшая механическая система — материальная точка в трёхмерном пространстве — обладает тремя степенями свободы, так как её состояние полностью описывается тремя пространственными координатами.
- Абсолютно твёрдое тело обладает шестью степенями свободы, так как для полного описания положения такого тела достаточно задать три координаты центра масс и три угла, описывающих ориентацию тела (эти величины известны в быту как «наклон, подъём, поворот», в авиации их называют «крен, тангаж, рыскание»).
- Реальные тела обладают огромным числом степеней свободы (порядка числа частиц, из которых состоит тело). Однако в большинстве ситуаций оказывается, что наиболее важны лишь несколько «коллективных» степеней свободы, характеризующих движение центра масс тела, его вращение, его деформацию, его макроскопические колебания. Остальные же — микроскопические — степени свободы не заметны по отдельности, а воспринимаются сразу все вместе, как, например, температура и давление.
Обобщённые координаты
Понятие степени свободы связано с таким понятием, как размерность. В математике размерность — это количество независимых параметров, необходимых для описания состояния объекта, или, другими словами, для определения его положения в неком абстрактном пространстве.
При математическом описании состояния физической системы N степеням свободы отвечают N независимых переменных, называемых обобщёнными координатами.
В случае непрерывных степеней свободы соответствующие обобщённые координаты принимают непрерывный ряд значений. Однако можно рассматривать и дискретные степени свободы.
Примеры
- Для того, чтобы описать положение окружности на плоскости, достаточно трёх параметров: двух координат центра и радиуса, то есть пространство окружностей на плоскости трёхмерно. Окружность может быть перемещена в любую точку плоскости и её радиус может быть изменён, поэтому у неё три степени свободы.
- Для того, чтобы определить координаты объекта на географической карте, нужно указать широту и долготу. Соответствующее пространство поэтому называется двумерным. Объект может располагаться в любой точке, поэтому у каждого объекта на карте две степени свободы.
- Для задания положения самолёта нужно указать три координаты — дополнительно к широте и долготе нужно знать высоту, на которой он находится. Поэтому пространство, в котором находится самолёт, является трёхмерным. К этим трём координатам может быть добавлена четвёртая (время) для описания не только текущего положения самолёта, но и момента времени. Если добавить в модель ориентацию (крен, тангаж, рыскание) самолёта, то добавятся ещё три координаты и соответствующее абстрактное пространство модели станет семимерным.
Степени свободы в статистической физике и термодинамике
В статистической физике и термодинамике говоря о степенях свободы иногда имеют в виду тесно связанное с описанным выше, но несколько модифицированное понятие.
Дело в том, что в этом случае прежде всего интересует полная энергия, приходящаяся на степень свободы. А у каждой колебательной степени свободы имеется как кинетическая, так и потенциальная энергия.
Классическая теорема о распределении энергии по степеням свободы[2] гласит: при термодинамическом равновесии кинетическая энергия в среднем равномерно распределяется по всем степеням свободы, по kT/2 на каждую степень свободы. При этом на каждую степень свободы, имеющую и потенциальную энергию (зависящую от данной координаты), потенциальная энергия также добавляется к полной энергии системы, а для колебательных степеней свободы средняя кинетическая и средняя потенциальная энергия равны (это утверждение является точным для гармонических осцилляторов, однако является хорошим приближением и при некотором ангармонизме).
Таким образом, оказывается, что при вычислении внутренней энергии системы каждая колебательная степень свободы учитывается дважды. Поэтому иногда, для простоты подсчетов используют формулу
где под понимают количество степеней свободы не в обычном смысле, а в смысле распределения полной энергии, то есть каждая колебательная степень свободы учитывается дважды (как «колебательная кинетическая» плюс как «колебательная потенциальная», то есть в этом смысле можно говорить, что каждой колебательной степени свободы соответствуют две степени свободы в термодинамическом смысле. Остальные степени свободы (поступательные и вращательные) учитываются просто, без удвоения (так как этим видам движения соответствует нулевая — говоря точнее, пренебрежимо малая — потенциальная энергия).
Таким образом, в статистической физике нередко под степенями свободы понимают координаты не в конфигурационном пространстве, а в фазовом пространстве, т.е. считают за различные степени свободы обобщенные координаты и обобщенные импульсы. В этом случае вносят одинаковый в классическом приближении (т.е. с некоторыми оговорками — просто при достаточно высоких температурах) вклад в полную энергию — по каждая — только те из них, которые входят в выражение для энергии квадратически.
Вымораживание степеней свободы
Квантовомеханическое рассмотрение показывает, что разные степени свободы могут быть активны или неактивны вот в каком смысле. Если некоторое движение имеет дискретный спектр (а дискретный спектр соответствует всякому связанному состоянию), то оно может возбуждаться (система переходить на более высокий энергетический уровень) только при поглощении энергии большей, чем разность энергии первого возбужденного и основного состояния (энергии возбуждения). Поэтому если система (молекула, атом) вначале находится в основном состоянии и происходит взаимодействие с частицей, которая может отдать лишь энергию меньшую, чем энергия возбуждения (например с фотоном более низкой энергии или с молекулой, энергия движения которой меньше, чем этот порог) данная степень свободы никак не проявляется (движение, связанное с ней, не может возникнуть; говоря точнее, оно не может измениться, эта степень свободы остается в основном состоянии). Это называется вымораживанием степени свободы (конечно же, даже у одной и той же системы разные степени свободы могут иметь одинаковые или разные энергии возбуждения, и поэтому быть вымороженными или не вымороженными для взаимодействия с частицами разных энергий).
Это в полной мере относится к проявлению разных степеней свободы при различных температурах.
Действительно, при определенной температуре энергия движения частиц имеет в среднем величину порядка kT, следовательно все степени свободы, энергия возбуждения которых много больше, будут выморожены (их можно не учитывать в статистике). В связи с этим для каждой конкретной степени свободы каждой системы (атома, молекулы, кристалла и т. д.) вводится понятие температуры вымораживания (равной энергии возбуждения, деленной на постоянную Больцмана). При температурах много ниже температуры вымораживания степень свободы не проявляется (находится в основном состоянии и обычно может просто никак не учитываться), при много больших — степень свободы полностью «включена» и движение по ней может рассматриваться как классическое, при температурах же порядка температуры вымораживания происходит постепенное[3] включение степени свободы при повышении температуры или постепенное выключение при понижении.
Описанное объясняет изменение теплоемкости различных веществ с температурой. Классическая статистическая физика говорит о равномерном распределении энергии по степеням свободы (здесь термин степень свободы понимается в термодинамическом смысле, см. выше). Однако очевидно, что на самом деле (учитывая квантовомеханическую коррекцию) это утверждение следует относить только к «включенным» степеням свободы, то есть исключая вымороженные. Следовательно, молярная теплоемкость будет
где k — постоянная Больцмана, Nf — количество степеней свободы данного типа в рассматриваемой системе (в частности, если речь идет о совокупности молекул, где N — количество молекул, i — количество степеней свободы одной молекулы).
Степени свободы молекулы
Формула внутренней энергии газа:
- ,
и прямо связанная с ней формула для средней энергии молекулы газа
- ,
где
- — количество степеней свободы молекулы газа,
- — количество газа ( — масса, — молярная масса газа),
- — универсальная газовая постоянная,
- — константа Больцмана,
- — абсолютная температура газа,
— включают количество степеней свободы молекулы.
Степени свободы молекулы вымораживаются, как это описано в параграфе выше, что означает, что эффективное i в формуле зависит от температуры и, вообще говоря, не может быть просто вычислено классическим механическим способом.
Все вращательные степени свободы у одноатомных молекул и вращательная степень свободы, соответствующая вращению вокруг продольной оси у линейных (в реальном геометрическом смысле) молекул, выморожены (то есть не должны учитываться в i) всегда, поскольку их температуры вымораживания настолько высоки, что диссоциация молекул происходит гораздо раньше, чем эти температуры достигаются.
См. также
Примечания
- ↑ Подразумевая классическую динамику, здесь имеют в виду уравнения движения. Однако, по крайней мере в принципе, для квантового описания могут быть использованы практически совпадающие по форме операторные уравнения.
- ↑ Она верна в чистом виде только в классическом (то есть неквантовом) приближении, а при попытках вполне последовательного применения приводит к несоответствию опыту и даже парадоксам, таким как ультрафиолетовая катастрофа; однако остается важной и для квантового случая, хотя тогда ее формулировку следует сильно изменить. См. также дальше в данной статье (из чего следует, что при адекватном учете квантовых коррекций даже чисто классическая теорема может быть использована.
- ↑ Постепенное по причине плавности теплового распределения.
Степень свободы — это… Что такое Степень свободы?
- Степень свободы
Большая советская энциклопедия. — М.: Советская энциклопедия.
1969—1978.
- Степень окисления
- Степень сжатия
Смотреть что такое «Степень свободы» в других словарях:
Степень свободы — Степени свободы (физика) Степени свободы (механика) Степень свободы (кристаллография) число переменных, которые можно менять, не меняя фазового состояния системы. Степень свободы молекул количество координат для определения… … Википедия
степень свободы — laisvės laipsnis statusas T sritis fizika atitikmenys: angl. degree of freedom vok. Freiheitsgrad, m rus. степень свободы, f pranc. degré de liberté, m … Fizikos terminų žodynas
степень свободы — 2.85. степень свободы В общем случае число слагаемых минус число ограничений, налагаемых на них Источник: ГОСТ Р 50779.10 2000: Статистические методы. Вероятность и основы статистики. Термины и определения … Словарь-справочник терминов нормативно-технической документации
степень свободы — стадия полимеризации, степень полимеризации … Cловарь химических синонимов I
Степень свободы — в механике см. Свобода движения … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
СТЕПЕНЬ СВОБОДЫ ВСТРЯХИВАЮЩИХ МЕХАНИЗМОВ ФОРМОВОЧНЫХ МАШИН — независимые движения цилиндров встряхивающего механизма. Различают встряхивающие механизмы с одной и двумя степенями свободы (рис. С 21). Рис. С 21. Встряхивающие механизмы с одной (а) и двумя (б) степенями свободы … Металлургический словарь
статистическая степень свободы — 3.34 статистическая степень свободы (statistical degrees of freedom): Величина, характеризующая свойства оценки спектральной плотности ускорения, получаемой по случайным отсчетам методом усреднения по времени, и зависящая от разрешения по частоте … Словарь-справочник терминов нормативно-технической документации
вращательная степень свободы — sukimosi laisvės laipsnis statusas T sritis fizika atitikmenys: angl. rotational degree of freedom vok. Rotationsfreiheitsgrad, m rus. вращательная степень свободы, f pranc. degré de liberté de rotation, m … Fizikos terminų žodynas
колебательная степень свободы — virpesių laisvės laipsnis statusas T sritis fizika atitikmenys: angl. vibrational degree of freedom vok. Schwingungsfreiheitsgrad, m rus. колебательная степень свободы, f pranc. degré de liberté de vibration, m … Fizikos terminų žodynas
колебательная степень свободы — svyravimų laisvės laipsnis statusas T sritis fizika atitikmenys: angl. oscillational degree of freedom; vibrational degree of freedom vok. Schwingungsfreiheitsgrad, m rus. колебательная степень свободы, f pranc. degré de liberté oscillatoire, m … Fizikos terminų žodynas
СТЕПЕНИ СВОБОДЫ — это… Что такое СТЕПЕНИ СВОБОДЫ?
- СТЕПЕНИ СВОБОДЫ
- СТЕПЕНИ СВОБОДЫ
-
независимые возможные изменения состояния (в частности, положения) физ. системы, обусловленные вариациями её параметров. В механике С. с. соответствуют независимым перемещениям механич. системы, число к-рых определяется числом образующих систему ч-ц и наложенных на неё механич. связей (см. СТЕПЕНЕЙ СВОБОДЫ ЧИСЛО). В статистической физике С. с. соответствуют независимым обобщённым координатам, определяющим полную энергию или Гамильтона функцию системы. Число С. с. позволяет оценить теплоёмкость многоат. газов и тв. тел при высоких темп-рах, когда применима классич. статистич. механика и энергия равномерно распределена по С. с. (равнораспределения закон). Однако при обычных (комнатных) темп-рах не все С. с. вносят вклад в теплоёмкость многоат. газа, нек-рые из них «выключены», т. к. могут возбуждаться лишь при достаточно высоких темп-рах. В квантовой механике С. с. соответствуют независимым координатам, к-рые определяют гамильтониан системы. Непрерывные поля нельзя охарактеризовать конечным числом С. с.В термодинамике С. с.— независимые термодинамич. параметры. определяющие состояние термодинамич. равновесия системы. Число С. с. / равновесной термодинамич. системы определяется Гиббса правилом фаз: f=k-j+2, где k — число компонентов, j — число фаз.
Физический энциклопедический словарь.
— М.: Советская энциклопедия.
Главный редактор А. М. Прохоров.
1983.- СТЕПЕНИ СВОБОДЫ
-
— независимые возможные изменения состояния (вчастности, положения) физ. системы, обусловленные вариациями её параметров. Степеней свободы число в механике).
В статистической физике С. с. соответствуют независимым обобщённымкоординатам, определяющим полную энергию или Гамильтона функцию системы. теплоёмкость многоатомных газов итвёрдых тел при высоких темп-pax, когда применима классич. статистич. механикаи энергия равномерно распределена на С. с. ( равнораспределения закон). Однако при обычных (комнатных) темп-pax не все С. с. вносят вклад втеплоёмкость многоатомного газа, нек-рые из них выключены («заморожены»),т. к. могут возбуждаться лишь при достаточно высоких темп-рах.
В квантовой механике С. с. соответствуют независимым координатам, гамильтониан, системы. Непрерывные поля нельзяохарактеризовать конечным числом С. с.
В термодинамике С. с.- независимые термодинамич. параметры, определяющиесостояние термодинамич. равновесия системы. Число С. с. f равновеснойтермодинамич. системы определяется Гиббса правилом фаз:
 , где n — число компонентов, r — число фаз. д. н. Зубарев.
, где n — число компонентов, r — число фаз. д. н. Зубарев.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия.
Главный редактор А. М. Прохоров.
1988.
.
- СТЕПЕНЕЙ СВОБОДЫ ЧИСЛО
- СТЕРАДИАН
Смотреть что такое «СТЕПЕНИ СВОБОДЫ» в других словарях:
СТЕПЕНИ СВОБОДЫ — (1) в механике независимые возможные виды движения твёрдого тела, количество которых определяется числом наложенных механических связей () для данной системы. Наложение связей приводит к уменьшению числа степеней свободы системы. Напр. свободная… … Большая политехническая энциклопедия
СТЕПЕНИ СВОБОДЫ — 1) в механике независимые между собой возможные перемещения механической системы. Число степеней свободы зависит от числа материальных частиц, образующих систему, и числа и характера наложенных на систему связей механических. Так, свободное… … Большой Энциклопедический словарь
СТЕПЕНИ СВОБОДЫ — (degrees of freedom) Число независимых переменных в каком либо множестве. Например, если N переменных xi (i=1, 2,…,N) должны иметь среднее, равное m, тогда существует только N–1 степеней свободы, поскольку, если N–1 переменных выбраны… … Экономический словарь
СТЕПЕНИ СВОБОДЫ — англ. freedom, degree of; нем. Freiheitsgrade. В статист, вычислениях максимальное число значений переменной (или переменных), к рые могут свободно изменяться при данном наборе условий. Antinazi. Энциклопедия социологии, 2009 … Энциклопедия социологии
Степени свободы — [degrees of freedom] 1. В анализе систем линейных уравнений разность между числом независимых уравнений и числом неизвестных. Если число С. с. равно нулю, то система имеет единственное решение. 2. В математической статистике числа, показывающие… … Экономико-математический словарь
Степени свободы — У этого термина существуют и другие значения, см. Свобода (значения). У этого термина существуют и другие значения, см. Степени свободы (механика). Степени свободы характеристики движения механической системы. Число степеней свободы… … Википедия
степени свободы — 1) в механике независимые между собой возможные перемещения механической системы. Число степеней свободы зависит от числа материальных частиц, образующих систему, и числа и характера наложенных на систему связей механических. Так, свободное… … Энциклопедический словарь
СТЕПЕНИ СВОБОДЫ (DF) — Математическое понятие, используемое для выражения того факта, что в статистических операциях имеются пределы значений, которые каждый свободен выбрать, накладывающие определенные ограничения на ситуацию. Предел определяется числом имеющихся… … Толковый словарь по психологии
степени свободы — термодинамические степени свободы; степени свободы Независимые термодинамические параметры фаз системы, находящейся в равновесии, изменение которых в определенных пределах не вызывает исчезновения одних и образования других фаз … Политехнический терминологический толковый словарь
степени свободы — laisvės laipsniai statusas T sritis augalininkystė apibrėžtis Laisvai varijuojančių pasirinktos visumos duomenų, kurie charakterizuojami jų aritmetiniu vidurkiu, skaičius (df). atitikmenys: angl. degree of freedom rus. степени свободы … Žemės ūkio augalų selekcijos ir sėklininkystės terminų žodynas
Степени свободы (значения) — это… Что такое Степени свободы (значения)?
- Степени свободы (значения)
Категория:
- Многозначные термины
Wikimedia Foundation.
2010.
- Степашкин, Станислав Иванович
- Четыре степени жестокости
Смотреть что такое «Степени свободы (значения)» в других словарях:
Степени свободы (физика) — У этого термина существуют и другие значения, см. Свобода (значения). У этого термина существуют и другие значения, см. Степени свободы (значения). Степени свободы характеристики движения механической системы. Число степеней свободы… … Википедия
Степени свободы (механика) — У этого термина существуют и другие значения, см. Степени свободы (значения). В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена … Википедия
Степени свободы (теория вероятностей) — У этого термина существуют и другие значения, см. Степени свободы (значения). Количество степеней свободы это количество значений в итоговом вычислении статистики, способных варьироваться. Иными словами, количество степеней свободы… … Википедия
СТЕПЕНИ СВОБОДЫ — (1) в механике независимые возможные виды движения твёрдого тела, количество которых определяется числом наложенных механических связей () для данной системы. Наложение связей приводит к уменьшению числа степеней свободы системы. Напр. свободная… … Большая политехническая энциклопедия
Степени свободы — [degrees of freedom] 1. В анализе систем линейных уравнений разность между числом независимых уравнений и числом неизвестных. Если число С. с. равно нулю, то система имеет единственное решение. 2. В математической статистике числа, показывающие… … Экономико-математический словарь
Степени свободы — У этого термина существуют и другие значения, см. Свобода (значения). У этого термина существуют и другие значения, см. Степени свободы (механика). Степени свободы характеристики движения механической системы. Число степеней свободы… … Википедия
Права и свободы человека и гражданина — Права Теория Естественные и законные права Права требования и права свободы Отрицательные и положительные права … Википедия
Адаптации осужденных к местам лишения свободы уровни — Имеет в исправительном аспекте несколько сторон (уровней): социальную, социально психологическую и психологическую. Под социальной адаптацией понимается знание осужденными своих прав и обязанностей в местах лишения свободы, знание и выполнение… … Энциклопедия современной юридической психологии
Орден Свободы (Украина) — У этого термина существуют и другие значения, см. Орден Свободы. Орден Свободы … Википедия
Орден Свободы (Португалия) — У этого термина существуют и другие значения, см. Орден Свободы. Орден Свободы … Википедия
Степени свободы (физика) — Карта знаний
- Сте́пени свобо́ды — характеристики движения механической системы. Число степеней свободы определяет минимальное количество независимых переменных (обобщённых координат), необходимых для полного описания состояния механической системы. Строгое теоретико-механическое определение: число степеней свободы механической системы есть размерность пространства её состояний с учётом наложенных связей.
Также число степеней свободы равно полному числу независимых уравнений второго порядка (таких, как уравнения Лагранжа) или половине числа уравнений первого порядка (таких, как канонические уравнения Гамильтона), полностью описывающих динамику системы.
Источник: Википедия
Связанные понятия
Теорема о равнораспределении кинетической энергии по степеням свободы, закон равнораспределения, теорема о равнораспределении — связывает температуру системы с её средней энергией в классической статистической механике. В первоначальном виде теорема утверждала, что при тепловом равновесии энергия разделена одинаково между её различными формами, например, средняя кинетическая энергия поступательного движения молекулы должна равняться средней кинетической энергии её вращательного движения.
Эне́ргия (др.-греч. ἐνέργεια — действие, деятельность, сила, мощь) — скалярная физическая величина, являющаяся единой мерой различных форм движения и взаимодействия материи, мерой перехода движения материи из одних форм в другие. Введение понятия энергии удобно тем, что в случае, если физическая система является замкнутой, то её энергия сохраняется в этой системе на протяжении времени, в течение которого система будет являться замкнутой. Это утверждение носит название закона сохранения энергии.
Вну́тренняя эне́ргия — принятое в физике сплошных сред, термодинамике и статистической физике название для той части полной энергии термодинамической системы, которая не зависит от выбора системы отсчета и которая в рамках рассматриваемой проблемы может изменяться. То есть для равновесных процессов в системе отсчета, относительно которой центр масс рассматриваемого макроскопического объекта покоится, изменения полной и внутренней энергии всегда совпадают. Перечень составных частей полной энергии…
Электри́ческий ди́польный моме́нт — векторная физическая величина, характеризующая, наряду с суммарным зарядом (и реже используемыми высшими мультипольными моментами), электрические свойства системы заряженных частиц (распределения зарядов) в смысле создаваемого ею поля и действия на неё внешних полей. Главная после суммарного заряда и положения системы в целом (её радиус-вектора) характеристика конфигурации зарядов системы при наблюдении её издали.
Упоминания в литературе
Разрушение «реликтовой» первичной холономной связи на квантовом уровне проявляется в явлении декогеренции – потере системой чисто квантовых свойств и её переходе из суперпозиционного квантового состояния в смешанное. Причиной тому КМ называет взаимодействие со средой. К этому можно, однако, добавить, что глубинной основой такого взаимодействия выступает наличие интенционально-эмапатического импульса. Механизм декогеренции КМ представляет как запутывание первоначального квантового состояния с таким большим числом степеней свободы окружения (т. е. в наших представлениях – противоречивым разнообразием множества воздействующих извне интенциональных импульсов), так что в усреднённой картине вклад интерференционных членов оказывается как бы случайным и близким к нулю. Математическое описание декогеренции в КМ аналогично суммированию огромного числа произвольно смещенных друг относительно друга синусоид и делением этой суммы на их полное число. Каждая из подобных синусоид отвечает вкладу в интерференцию одной степени свободы окружения, и чем степеней свободы больше, тем ближе к нулю итоговый результат. Сама же интерференция возникает как результат сложения колебаний с разными фазами, что математически похоже на суммирование смещенных друг относительно друга синусоид. Однако в эти аспекты квантово-механических репрезентаций нам нет необходимости погружаться. Важно лишь иметь в виду, что системы абсолютно изолированные (замкнутые) и никак не взаимодействующие с окружением могут существовать лишь теоретически или в только в импликативном мире. Хотя абсолютно изолированных систем не существует, для двух или более частей единой системы, не взаимодействовавших и не взаимодействующих друг с другом, можно указать промежуток времени, в течение которого допустимо их считать автономными.
Все ранее известные формулировки систем построены на принципе взаимодействия множества компонентов. Вместе с тем элементарные расчеты показывают, что простое взаимодействие огромного числа компонентов, например человеческого организма, ведет к бесконечно огромному числу степеней их свободы. Даже оценивая только число степеней свобод основных компонентов ЦНС, но принимая при этом во внимание наличие, по крайней мере, пяти возможных изменений в градации состояний нейрона [T. Bullock, 1958], можно получить совершенно фантастическую цифру с числом нулей на ленте длиной более 9 км [П. К. Анохин, 1978]. То есть простое взаимодействие компонентов реально не является фактором, объединяющим их в систему. Именно поэтому в большинство формулировок систем входит термин «упорядочение». Однако, вводя этот термин, необходимо понять, что же «упорядочивает» «взаимодействие» компонентов системы, что объединяет эти компоненты в систему, что является системообразующим фактором.
При усилении происходит взаимодействие квантовой системы (находящейся в состоянии суперпозиции) с другими системами (или степенями свободы), вызывающее запутывание (квантовую корреляцию) с ними. Затем и исходная система, и уже запутанные с ней взаимодействуют с еще большим количеством систем, вовлекая и их в запутанное состояние. Так происходит до тех пор, пока не образуется свойство, включающее огромное число систем или, по крайней мере, огромное число степеней свободы.
Для того чтобы лучше понять основные результаты взаимопроникновения и взаимообогащения дифференциальной психофизиологии и дифференциальной психологии, рассмотрим вначале предпосылки их сближения. К 1980 г. фактически уже была решена проблема парциальности свойств нервной системы, поставленная Небылицыным в 1968 г. (Небылицын, 1976). Показано, что парциальность существует только на уровне отдельных элементов и структур мозга, но исчезает при рассмотрении свойств на уровне целого мозга. Разработан ряд электрофизиологических методов, позволивших получить интегральные (общемозговые) нейродинамические характеристики, которые гипотетически были отнесены к категории общих свойств нервной системы (Русалов, 1979). Так, с помощью метода вызванных потенциалов было выделено свойство «стохастичность нейронных сетей мозга», выраженное в показателях вариабельности вызванных потенциалов. Это свойство отражает конституционно заданное «число степеней свободы» нейронных связей (по П. К. Анохину) и, возможно, такое общее свойство нервной системы, как подвижность на уровне целого мозга.
Важной особенностью современного города является тот факт, что его функционирование, с одной стороны, детерминировано социально-экономическими закономерностями и морально-правовыми нормами, а с другой, определяется хаотической динамикой его элементов (отдельные жители, организации, информационные и транспортные потоки и т. п.), которые имеют значительное число степеней свободы. Такое поведение сложной нелинейной системы в синергетике называется детерминированным хаосом. Математическим образом детерминированных хаотических движений является особый тип фрактальных образований – так называемый «странный аттрактор». Под аттрактором понимают геометрический образ движения, соответствующий определенному типу поведения реальной системы. При этом геометрическим образом равновесия в синергетике служит точка, а изображением периодического движения – замкнутая кривая, называемая предельным циклом. Аттракторы представляют собой относительно устойчивые состояния (или динамические траектории) системы (в нашем случае города), которые «притягивают» к себе множество других траекторий/состояний системы, определяемых разными начальными условиями.
Связанные понятия (продолжение)
Пе́рвое нача́ло термодина́мики (первый закон термодинамики) — один из основных законов этой дисциплины, представляющий собой конкретизацию общефизического закона сохранения энергии для термодинамических систем, в которых необходимо учитывать термические, массообменные и химические процессы. В форме закона сохранения (уравнения баланса энергии) первое начало используют в термодинамике потока и в неравновесной термодинамике. В равновесной термодинамике под первым законом термодинамики обычно подразумевают…
Согласно концепции переме́нной ско́рости све́та (ПСС) считается, что скорость света в вакууме, обычно обозначаемая c, в некоторых случаях может не быть константой. В большинстве ситуаций в физике конденсированного состояния распространение света в среде действительно происходит с меньшей скоростью, чем в вакууме. Кроме того, в некоторых расчётах квантовой теории поля необходимо учитывать, что виртуальные фотоны должны двигаться на короткие расстояния в том числе со скоростью, отличной от скорости…
Подробнее: Переменная скорость света
Потенциал Леннард-Джонса (потенциал 6-12) — простая модель парного взаимодействия неполярных молекул, описывающая зависимость энергии взаимодействия двух частиц от расстояния между ними. Эта модель достаточно реалистично передаёт свойства реального взаимодействия сферических неполярных молекул и поэтому широко используется в расчётах и при компьютерном моделировании. Впервые этот вид потенциала был предложен Леннард-Джонсом в 1924 году.
Принцип неопределённости Гейзенбе́рга (или Га́йзенберга) в квантовой механике — фундаментальное соображение (соотношение неопределённостей), устанавливающее предел точности одновременного определения пары характеризующих систему квантовых наблюдаемых, описываемых некоммутирующими операторами (например, координаты и импульса, тока и напряжения, электрического и магнитного полей). Более доступно он звучит так: чем точнее измеряется одна характеристика частицы, тем менее точно можно измерить вторую…
Конденса́т Бо́зе — Эйнште́йна (бо́зе-эйнште́йновский конденса́т, бо́зе-конденса́т) — агрегатное состояние вещества, основу которого составляют бозоны, охлаждённые до температур, близких к абсолютному нулю (меньше миллионной доли кельвина). В таком, сильно охлаждённом, состоянии достаточно большое число атомов оказывается в своих минимально возможных квантовых состояниях и квантовые эффекты начинают проявляться на макроскопическом уровне.
Дина́мика (греч. δύναμις «сила, мощь») — раздел механики, в котором изучаются причины возникновения механического движения. Динамика оперирует такими понятиями, как масса, сила, импульс, момент импульса, энергия.
Переход Костерлица — Таулеса или переход Березинского — Костерлица — Таулеса (БКТ-переход) или топологический фазовый переход — фазовый переход в двумерной XY-модели. Это переход из состояния связанных пар вихрь-антивихрь при низких температурах в состояние с неспаренными вихрями и антивихрями при некоторой критической температуре. Переход назван в честь занимающихся конденсированными средами физиков Вадима Львовича Березинского, Джона М. Костерлица и Дэвида Дж. Таулеса. БКТ-переходы можно наблюдать…
Внутренняя энергия термодинамической системы может изменяться двумя способами: посредством совершения работы над системой и посредством теплообмена с окружающей средой. Энергия, которую получает или теряет тело в процессе теплообмена с окружающей средой, называется коли́чеством теплоты́ или просто теплотой. Теплота — это одна из основных термодинамических величин в классической феноменологической термодинамике. Количество теплоты входит в стандартные математические формулировки первого и второго…
Подробнее: Теплота
Закон сохранения массы — закон физики, согласно которому масса физической системы сохраняется при всех природных и искусственных процессах.
Специа́льная тео́рия относи́тельности (СТО; также называемая ча́стная тео́рия относи́тельности) — теория, описывающая движение, законы механики и пространственно-временные отношения при произвольных скоростях движения, меньших скорости света в вакууме, в том числе близких к скорости света (в рамках специальной теории относительности классическая механика Ньютона является приближением низких скоростей). Фактически СТО описывает геометрию четырёхмерного пространства-времени и базируется на плоском…
Адиабатическая теорема — теорема квантовой механики. Впервые была сформулирована Максом Борном и Владимиром Фоком в 1928 году в таком виде…
Поверхность потенциальной энергии применяется для описания энергии системы, в особенности множества атомов, в терминах определённых параметров, обычно — координат атомов. Поверхность может определять энергию как функцию одной или нескольких координат. Если координата только одна, то поверхность называется кривой потенциальной энергии или профилем энергии.
Теоре́ма о кинети́ческой эне́ргии систе́мы — одна из общих теорем динамики, является следствием законов Ньютона. Связывает кинетическую энергию механической системы с работой сил, действующих на тела, составляющие систему. В качестве системы, о которой идёт речь, может выступать любая механическая система, состоящая из любых тел.
Гравитация с массивным гравитоном — название класса теорий гравитации, в которых частица-переносчик взаимодействия (гравитон) предполагается массивной, примером является релятивистская теория гравитации. Характерная особенность таких теорий — проблема разрыва ван Дама — Вельтмана — Захарова (англ. vDVZ (van Dam-Veltman-Zakharov) discontinuity), то есть наличие конечной разности в предсказаниях предела такой теории при массе гравитона, стремящейся к нулю, и теории с безмассовой частицей с самого начала…
Второе начало термодинамики (второй закон термодинамики) устанавливает существование энтропии как функции состояния термодинамической системы и вводит понятие абсолютной термодинамической температуры, то есть «второе начало представляет собой закон об энтропии» и её свойствах. В изолированной системе энтропия остаётся либо неизменной, либо возрастает (в неравновесных процессах), достигая максимума при установлении термодинамического равновесия (закон возрастания энтропии). Встречающиеся в литературе…
Ста́рая ква́нтовая тео́рия (иногда ста́рая ква́нтовая меха́ника) — подход к описанию атомных явлений, который был развит в 1900—1924 годах и предшествовал квантовой механике. Характерная черта теории — использование классической механики и некоторых предположений, вступавших в противоречие с ней. Основа старой квантовой теории — модель атома Бора, к которой позже Арнольд Зоммерфельд добавил квантование z-компоненты углового момента, которое неудачно назвали пространственным квантованием. Квантование…
Радиационное трение, реакция излучения, лучистое трение, торможение излучением — сила, действующая на заряженную точечную частицу (например, электрон), со стороны её собственного электромагнитного излучения, вызываемого неравномерностью движения этой частицы.
Си́ла — физическая векторная величина, являющаяся мерой воздействия на данное тело со стороны других тел или полей. Приложение силы обусловливает изменение скорости тела или появление деформаций и механических напряжений.
Автоволны (англ. autowaves) — это самоподдерживающиеся нелинейные волны в активных средах (то есть содержащих распределённые источники энергии). Термин в основном применяется к процессам, где волной переносится относительно малая энергия, которая необходима для синхронизации или переключения активной среды.
Термодина́мика (греч. θέρμη — «тепло», δύναμις — «сила») — раздел физики, изучающий наиболее общие свойства макроскопических систем и способы передачи и превращения энергии в таких системах. В термодинамике изучаются состояния и процессы, для описания которых можно ввести понятие температуры. Термодинамика — это феноменологическая наука, опирающаяся на обобщения опытных фактов. Процессы, происходящие в термодинамических системах, описываются макроскопическими величинами (температура, давление, концентрации…
В физике, предел Бекенштейна — это верхний предел энтропии S, или количества информации I, которые могут содержаться в заданной ограниченной области пространства, имеющей конечное количество энергии; либо, с другой стороны, максимальное количество информации, необходимое для идеального описания заданной физической системы вплоть до квантового уровня. Это подразумевает, что информация о физической системе, или информация, необходимая для идеального описания системы, должна быть конечной, если система…
Простра́нство-вре́мя (простра́нственно-временно́й конти́нуум) — физическая модель, дополняющая пространство равноправным временны́м измерением и таким образом создающая теоретико-физическую конструкцию, которая называется пространственно-временным континуумом. Пространство-время непрерывно и с математической точки зрения представляет собой многообразие с лоренцевой метрикой.
Одноро́дность времени — означает, что все моменты времени равноправны, то есть что если в два любые момента времени все тела замкнутой системы поставить в совершенно одинаковые условия, то начиная с этих моментов все явления в ней будут проходить совершенно одинаково. Однородность — одно из ключевых свойств времени в классической механике. Является фундаментальным обобщением опытных фактов.Все известные законы природы, в том числе для живой материи, подтверждают равномерность хода времени. Например…
Закон соответственных состояний гласит, что все вещества подчиняются одному уравнению состояния, если это уравнение выразить через приведённые переменные. Этот закон является приближённым и позволяет достаточно просто оценивать свойства плотного газа или жидкости с точностью порядка 10—15 %. Первоначально был сформулирован Ван дер Ваальсом в 1873 году.
Теория среднего поля или теория самосогласованного поля — подход к изучению поведения больших и сложных стохастических систем в физике и теории вероятностей через исследование простых моделей. Такие модели рассматривают многочисленные малые компоненты, которые взаимодействуют между собой. Влияние других индивидуальных компонент на заданный объект аппроксимируется усредненным эффектом, благодаря чему задача многих тел сводится к одночастичной задаче.
Метастабильное состояние (от греч. μετα «через» и лат. stabilis «устойчивый») — состояние квазиустойчивого равновесия физической системы, в котором система может находиться длительное время.
Возникнове́ние ква́нтовой фи́зики — процесс длительный и постепенный, который занял свыше 25 лет. От первого возникновения понятия кванта до разработки так называемой копенгагенской интерпретации квантовой механики прошло 27 лет, заполненных интенсивной работой учёных всей Европы. В развитии и понимании квантовой теории приняли участие очень многие люди, как старшего поколения — Макс Борн, Макс Планк, Пауль Эренфест, Эрвин Шрёдингер, так и совсем молодые, ровесники квантовой гипотезы — Вернер Гейзенберг…
Общее уравнение механики представляет собой математическую формулировку принципа Д’Аламбера — Лагранжа, дающего общий метод решения задач динамики и статики и являющегося одним из основных принципов теоретической механики.( Стр.142) Этот принцип объединяет принцип возможных перемещений и принцип Д’Аламбера…
Сверхсветово́е движе́ние — движение со скоростью, превышающей скорость света в вакууме. Несмотря на то, что согласно специальной теории относительности скорость света в вакууме является максимально достижимой скоростью распространения сигналов, а энергия частицы положительной массы стремится к бесконечности при приближении её скорости к скорости света, объекты, движение которых не связано с переносом информации (например, фаза колебаний в волне, тень или солнечный зайчик), могут иметь сколь угодно…
Атом Гука относится к искусственным атомам подобных атому гелия, в котором кулоновский электрон-ядерный потенциал взаимодействия…
Вселе́нная Фри́дмана (метрика Фридмана — Леметра — Робертсона — Уокера) — одна из космологических моделей, удовлетворяющих полевым уравнениям общей теории относительности (ОТО), первая из нестационарных моделей Вселенной. Получена Александром Фридманом в 1922. Модель Фридмана описывает однородную изотропную в общем случае нестационарную Вселенную с веществом, обладающую положительной, нулевой или отрицательной постоянной кривизной. Эта работа учёного стала первым основным теоретическим развитием…
В физике, при рассмотрении нескольких систем отсчёта (СО), возникает понятие сложного движения — когда материальная точка движется относительно какой-либо системы отсчёта, а та, в свою очередь, движется относительно другой системы отсчёта. При этом возникает вопрос о связи движений точки в этих двух системах отсчета (далее СО).
Подробнее: Сложное движение
Метод ренормализационной группы (также часто называемый методом ренормгруппы, методом РГ) в квантовой теории поля — итеративный метод перенормировки, в котором переход от областей с меньшей энергией к областям с большей вызван изменением масштаба рассмотрения системы.
Подробнее: Ренормализационная группа
Теоре́ма И́рншоу — теорема об электростатическом поле, сформулирована в XIX веке английским физиком Ирншоу в 1842 году.
Фе́рми-газ (или идеальный газ Фе́рми — Дира́ка) — газ, состоящий из частиц, удовлетворяющих статистике Ферми — Дирака, имеющих малую массу и высокую концентрацию. Например, электроны в металле. В первом приближении можно считать, что потенциал, действующий на электроны в металле, является постоянной величиной и благодаря сильному экранированию положительно заряженными ионами можно пренебречь электростатическим отталкиванием между электронами. Тогда электроны металла можно рассматривать как идеальный…
При́нцип наиме́ньшего де́йствия Га́мильтона (также просто принцип Гамильтона), точнее при́нцип стациона́рности де́йствия — способ получения уравнений движения физической системы при помощи поиска стационарного (часто — экстремального, обычно, в связи со сложившейся традицией определения знака действия, наименьшего) значения специального функционала — действия. Назван в честь Уильяма Гамильтона, использовавшего этот принцип для построения так называемого гамильтонова формализма в классической механике…
Бро́уновское движе́ние (бра́уновское движе́ние) — беспорядочное движение микроскопических видимых взвешенных в жидкости или газе частиц твёрдого вещества, вызываемое тепловым движением частиц жидкости или газа. Было открыто в 1827 году Робертом Броуном (правильнее Брауном). Броуновское движение никогда не прекращается. Оно связано с тепловым движением, но не следует смешивать эти понятия. Броуновское движение является следствием и свидетельством существования теплового движения.
Фоковское состояние— это квантовомеханическое состояние с точно определённым количеством частиц. Названо в честь советского физика В. А. Фока.
Комплекс задач о взаимодействии многих тел достаточно обширный и является одним из базовых, далеко не полностью разрешённых, разделов механики. В рамках ньютоновской концепции проблема ветвится на…
Подробнее: Взаимодействие многих тел
Осцилляции Зенера — Блоха — колебания частицы, движущейся в периодическом потенциале, под действием постоянной силы. Примером системы, в которой могут реализоваться такие колебания, является кристаллическое твердое тело. В реальных кристаллах создать условия для наблюдения осцилляций Зенера — Блоха трудно, однако они наблюдались в искусственных системах, например, сверхрешётках.
M-тео́рия — современная физическая теория, созданная с целью объединения фундаментальных взаимодействий. В качестве базового объекта используется так называемая «брана» (многомерная мембрана) — протяжённый двухмерный или с бо́льшим числом измерений (n-брана) объект.
Подробнее: М-теория
Вре́мя — форма протекания физических и психических процессов, условие возможности изменения. Одно из основных понятий философии и физики, мера длительности существования всех объектов, характеристика последовательной смены их состояний в процессах и самих процессов, изменения и развития, а также одна из координат единого пространства-времени, представления о котором развиваются в теории относительности.
Тахио́н (от греч. ταχύς, «быстрый») — гипотетическая частица, движущаяся со скоростью, превышающей скорость света в вакууме, в противоположность обычным частицам, называемым в теоретических работах по тахионам тардионами, движущимся всегда медленнее света, способным покоиться, и люксонам (например, фотону), движущимся всегда только со скоростью света.
Релятивистская механика — раздел физики, рассматривающий законы механики (законы движения тел и частиц) при скоростях, сравнимых со скоростью света. При скоростях значительно меньших скорости света переходит в классическую (ньютоновскую) механику.
Фазовые переходы второго рода — фазовые переходы, при которых вторые производные термодинамических потенциалов по давлению и температуре изменяются скачкообразно, тогда как их первые производные изменяются постепенно. Отсюда следует, в частности, что энергия и объём вещества при фазовом переходе второго рода не изменяются, но изменяются его теплоёмкость, сжимаемость, различные восприимчивости и т. д.
Упоминания в литературе (продолжение)
Как материальную точку человека рассматривают тогда, когда его перемещения намного больше собственных размеров тела и когда не исследуют движения отдельных частей тела и его вращение. Например, при прыжке с парашютом (рис. 5) парящий под куполом человек может рассматриваться как точка, положение которой в неподвижной системе координат XYZ определяется тремя независимыми координатами х1, у1, z1. То есть в данном случае человек обладает тремя степенями свободы.
Итак, в физике, философии, биологии гибкость, в общем, определяют как количество степеней свободы. Свобода в свою очередь представляет собой число независимых видов движений, которые может совершать тело.[37] Применительно к живым системам, степенью свободы называют такую деятельность, которая формируется в порядке выбора из многих других возможных деятельностей этой системы. Поскольку выбор – это центральный момент в деятельности менеджера, то гибкость ключевое качество, определяющее его эффективность.
Статистический анализ спектров мощности по указанным диапазонам ЭЭГ при сравнении отдельных условий проводился с помощью двухфакторного дисперсионного анализа для повторных измерений с факторами «группа детей» (число уровней – 3 и 2) и «локализация электродов» (число уровней – 16). Для учета несферичности ковариационной матрицы выполнялась коррекция числа степеней свободы методом, предложенным Гринхаузом и Гейсером (цит. по: Keselman, Rogan, 1981).
Взаимодействие неразрывно связано с понятием физического поля. Под физическим полем понимается особая форма материи. Физическое поле рассматривается как система с бесконечным числом степеней свободы. Источниками физических полей в природе являются частицы вещества. Физические поля переносят взаимодействие между частицами с конечной скоростью.
Обзор новых направлений в науке будет неполным, если не отметить работу Артура Янга (Young, 1976 а, 1976 в). Его теория процессов серьезно претендует на роль будущей научной метапарадигмы. Она организует и самым исчерпывающим образом объясняет данные из ряда дисциплин: геометрии, квантовой теории и теории относительности, химии, биологии, ботаники, зоологии, психологии и истории, объединяя их во всеобъемлющее космологическое видение. Модель Вселенной Янга имеет четыре уровня, определяемые степенями свободы и ограниченности, и семь последовательных ступеней: свет, ядерные частицы, атомы, молекулы, растения, животные и люди. Янгу удалось открыть фундаментальный паттерн вселенского процесса, повторяющийся вновь и вновь на различных уровнях эволюции в природе. Кроме широких возможностей объяснения явлений, эта концепция обладает возможностями их предсказания.
В случае нахождения в точке , т. е. оптимальном пространстве состояний ?opt, биосистема обеспечивает свое максимальное внутривидовое и межвидовое разнообразие, которое оценивается числом степеней свободы, или числом независимых виртуальных перемещений в фазовом пространстве вектора X. Этим определяется стратегия выживания биосистемы, оптимальная с позиции максимальной безопасности, или минимального риска смерти, т. е. реализации принципа минимального риска.
Важным моментом в этих методах является приближенная замена дифференциальных уравнений (1.6) в частных производных системой обыкновенных дифференциальных уравнений, характеризующих динамические свойства системы с конечным числом степеней свободы.
С определенного момента профессии встают наряду с сословиями, а потом начинают вытеснять их. Так функциональная дифференциация конкурирует с процессом стратификации общества по сословному признаку. О. Шпенглер подчеркивал принципиальное отличие этих процессов: «Особняком от подлинной сословной структуры стоят повсюду профессиональные классы ремесленников, чиновников, художников и рабочих… Их выделение основывается на чисто технических навыках, а значит, не на символике времени и пространства [выделено мной – Д. М.]; их традиции также ограничиваются техникой, а не собственными нравами или моралью, как-то сплошь и рядом присутствует в экономике и науке. Офицеры и судьи, поскольку они выводят себя от знати, – сословия, чиновники – профессия; ученый, поскольку он вышел из духовенства, принадлежит к сословию, художник же – профессия. Честолюбие и совесть связываются в одном случае с сословием, в другом – с достигнутым результатом. В совокупности всех первых присутствует нечто символическое, как бы оно ни было слабо, и оно отсутствует у вторых»[148]. Дополнительный смысл последним словам из приведенной цитаты Шпенглера придает Луман: «функциональная интеграция – инклюзия – снижает степени свободы»[149], т. е. возможности индивида к самореализации. Стратификационная дифференциация, по крайней мере, на начальном этапе, напротив – расширяет эти возможности, поскольку ей соответствует, как было показано, более высокий уровень личностного развития. Это качественное различие между двумя видами дифференциации, по сути, до сих пор оставалось незамеченным, что влекло путаницу при рассмотрении классовой структуры общества.
Познание индивидуальности представляет собой целостное, многокомпонентное, динамическое образование и характеризуется как процесс и результат. В.С. Мерлин сформулировал методологические принципы, которыми должен руководствоваться исследователь в процессе организации исследования целостной индивидуальности: «Любое устойчивое целостное образование в природе или обществе представляет собой саморазвивающуюся и саморегулируемую большую систему, определяемую взаимодействием необозримого множества условий. Саморегуляция и саморазвитие большой системы возможны лишь потому, что она состоит из нескольких относительно замкнутых подсистем, находящихся в иерархическом отношении друг к другу. Относительная замкнутость каждой подсистемы обеспечивает ее относительную автономность от других подсистем и тем самым достаточное количество степеней свободы в реакциях большой системы на многообразные внешние воздействия. Иерархическое соотношение подсистем обеспечивает их координацию и направленный характер деятельности большой системы»18.
Оценка неслучайности согласия мнений экспертов производилась с использованием ?2 – критерия Пирсона при числе степеней свободы f=(n−1), и заданном уровне значимости α = 0,05:
ТВОРЧЕСТВО ЧЕЛОВЕКА ЗАВИСИТ ОТ ЕГО ИНДИВИДУАЛЬНОГО РАЗВИТИЯ, ОТ ЕГО СОЗНАНИЯ, КОТОРОЕ ЯВЛЯЕТСЯ ФУНКЦИЕЙ СТЕПЕНЕЙ СВОБОДЫ, РАЗВИТИЯ ТОНКОМАТЕРИАЛЬНЫХ ОЩУЩЕНИЙ И ЧИСТОТЫ ДУШИ.
Степень свободы — определение степени свободы по The Free Dictionary
Я говорил всего несколько мгновений, когда почувствовал некоторую степень свободы, и говорил то, что хотел, с большой легкостью. Он не говорил со мной много, но когда он говорил, то это было с некоторой степенью свободы, открытости и доброты тоже. , это явно казалось интимным, он знал, что его слова были музыкой для моих ушей; и когда его взгляды встретились с моими, это было с улыбкой — может быть, самонадеянной — но, о! Этот график показывает долю каждой степени свободы.Следовательно, важные степени могут быть выбраны с помощью этого графика. Он не может использовать колебания решетки в качестве степени свободы. Следовательно, газообразное Солнце должно полагаться почти исключительно на поступательные и электронные степени свободы как приемники энергии. Оно охватывает системы с одной степенью свободы, системы с несколькими степенями свободы, системы с распределенными параметрами, случайные колебания и сейсмическую инженерию. OTIS4 — это программа моделирования точечных масс с тремя степенями свободы (3DOF) для одиночных транспортных средств.Тем не менее, два движения в комбинации могут быть использованы для обеспечения дополнительной степени свободы и поворота пиццы по горизонтали, сообщает New Scientist. Стратегия математической модели для адаптивного механизма подвески зависит от процесса разработки закона управления, от использования упрощенного модель движения, только с одной степенью свободы для тестирования алгоритмов управления с высокой степенью сложности, для составления расширенной модели движения с семью и более степенями свободы, для лучшего представления комфортных характеристик и безопасности при разработке полученные результаты.Юридическое признание союзов геев дорого обходится христианским организациям, которые в настоящее время утратили определенную степень свободы. Если штаты не сделают исключения из этих законов по религиозным убеждениям, однополые браки начнут вытеснять религиозные организации с публичных площадей. Таким образом, в этом примере нет степени свободы (1 — 1 = 0). , степень свободы получается из числа независимых повторных наблюдений, т. е. n-1.
,
r — Понимание степеней свободы в лаве
Переполнение стека
Товары
- Клиенты
- Случаи использования
Переполнение стека
Общественные вопросы и ответыКоманды
Частные вопросы и ответы для вашей командыпредприятие
Частные вопросы и ответы для вашего предприятияработы
Программирование и связанные с ним возможности технической карьерыТалант
Нанять технических талантовреклама
Обратитесь к разработчикам по всему миру
Загрузка…
- Авторизоваться
зарегистрироваться
.

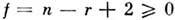 , где n — число компонентов, r — число фаз. д. н. Зубарев.
, где n — число компонентов, r — число фаз. д. н. Зубарев.